§ 6. Смешанное произведение

Рассмотрим операцию, соединяющую скалярное и векторное произведения.

Пусть даны три вектора а, b, c. Умножим b и с векторно. Полученный вектор [b, c] умножим скалярно на вектор а. В результате получим число (a, [b, c]).

Определение 21. Число (a, [b, c]) называется смешанным произведением векторов а, b, c и обозначается (a, b, c).

Свойства смешанного произведения:

1. Смешанное произведение некомпланарных векторов а, b, c по модулю равно объему параллелепипеда, построенного на сомножителях.

Действительно, по определению скалярного произведения

(a, b, c) = (a, [b, c]) = |a| ∙ |[b, c]| ∙ cosφ,

где φ – угол между векторами а и [b,c]. Учитывая, что |a| ∙ cosφ равно высоте параллелепипеда h, а модуль векторного произведения |[b,c]| равен площади параллелограмма, построенного на векторах b и с, получаем

(a, b, c) = S_осн ∙ h = V_паралл.

2. Смешанное произведение положительно, если тройка векторов а, b, c правая, и отрицательно, если она левая.

Действительно, знак смешанного произведения совпадает со знаком cosφ, и поэтому смешанное произведение положительно, когда а направлен в ту же сторону от плоскости векторов b и с, что и вектор [b, c], т. е. тройка векторов а, b, c правая. Если cosφ < 0, то вектор а направлен в противоположную сторону от плоскости векторов b и c по отношению к вектору [b, c] и, значит, тройка векторов а, b, c левая.

3. Если е₁, е₂, е₃ ортонормированный базис, то (е₁, е₂, е₃) = 1, если базис правый, и (е₁, е₂, е₃) = –1, если базис левый.

4. Смешанное произведение равно нулю тогда и только тогда, когда сомножители компланарны.

Учитывая (a, b, c) = |a| ∙ |[b, c]| ∙ cos φ, получаем, что смешанное произведение равно нулю в одном из следующих трех случаев:

а) а = 0, тогда а, b, c компланарны;

б) |[b, c]| = 0, тогда b и с коллинеарны, а, значит, а, b, c компланарны;

в) cosφ = 0, тогда вектор а лежит в плоскости векторов b и с, т. е. векторы а, b, c компланарны.

Если векторы а, b, c компланарны, то либо, по крайней мере, один из них нулевой и тогда ситуация рассмотрена в пунктах а) и б), либо все три вектора лежат в одной плоскости и выполняется пункт в).

Таким образом, равенство нулю смешанного произведения дает критерий компланарности векторов сомножителей.

5. Для любых векторов а, b, c верны равенства

(a, b, c) = (c, a, b) = (b, c, a) = – (b, a, c) = – (c, b, a) = – (a, c, b).

При перестановке сомножителей в смешанном произведении, самое большее, может измениться только ориентация тройки этих векторов. Поэтому, может измениться только знак смешанного произведения.

6. Для любых векторов а₁, а₂, b, c и чисел α, β верно равенство

(α а₁ + βа₂, b, c) = α (a₁, b, c) + β (a₂, b, c).

Это свойство следует из свойств скалярного произведения. С учетом предыдущего свойства получаем для векторов а, b₁, b₂, c и чисел α, β

(а, αb₁+ βb₂, c) = α (a, b₁, c) + β (a, b₂, c)

и для векторов а, b, с₁, c₂ и чисел α, β

(а, b, αc₁ + βс₂) = α (a, b, c₁) + β (a, b, c₂).

Таким образом, смешанное произведение линейно по любому своему сомножителю.

Найдем выражение смешанного произведения через координаты сомножителей. Пусть a = a₁i + a₂j + a₃k, b = b₁i + b₂j + b₃k, с = с₁i + с₂j + с₃k, где i, j, k – ортонормированный базис. Векторы i, j, k образуют правую тройку векторов. Тогда координаты векторного произведения [b, c] находятся по следующей формуле:

.

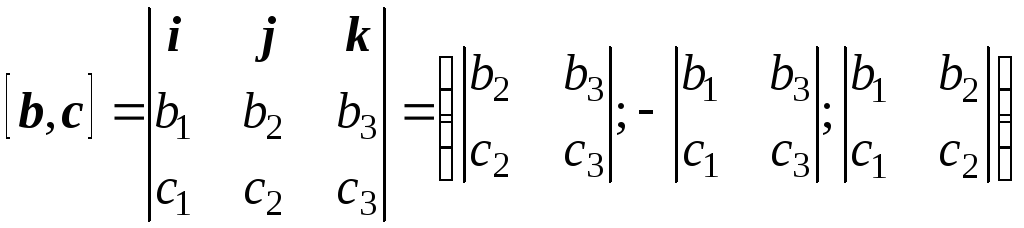Умножим этот вектор на вектор а по формуле скалярного произведения:

(a, [b, c]) = .

Поученное выражение можно рассматривать как разложение определителя третьего порядка по первой строке, в которой стоят координаты вектора а, алгебраическими дополнениями служат координаты векторного произведения. Следовательно, можно считать, что выражение смешанного произведения через координаты сомножителей имеет вид:

.

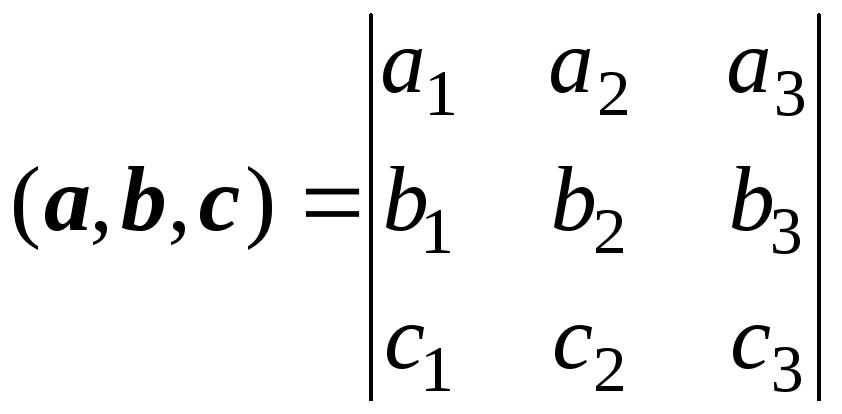Данная формула верна только в том случае, когда координаты векторов a, b, c заданы в ортонормированном базисе.