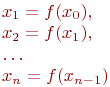- •1.Предмет и задачи информатики
- •1) Теоретическая информатика:
- •2) Средства информатизации:
- •3) Информационные технологии
- •4) Социальная информатика:
- •2. Истоки и предпосылки информатики.
- •3. Структура современной информатики
- •4. Понятие информации. Носители информации. Сигналы
- •5. Количество информации. Измерение информации. Единицы измерения
- •6. Кодирование информации различных видов
- •7. Свойства информации
- •8. Устройство персонального компьютера
- •9. Основные принципы построения и работы компьютера
- •10. Понятие файла и файловой системы
- •11. Понятие информационной технологии
- •13. Основы интернета. Основные протоколы
- •14. Службы Интернета
- •15. Этапы решения задачи на эвм
- •16. Алгоритм. Свойства алгоритма
- •17. Методы проектирования алгоритмов
- •18. Способы описания алгоритмов. Основы графического способа.
- •19. Структуры алгоритмов. Основные виды вычислительных процессов. Примеры.
- •20. Алгоритмы вычисления суммы функционального ряда. Использование рекуррентных формул. Пример
- •Примеры
- •21. Поиск минимального и максимального элементов массива.
- •22. Сортировка одномерных массивов
- •23. Системы программирования и их состав.
- •24. Понятие о программировании
- •25. Понятие программного обеспечения. Классификация программного обеспечения.
- •26. Назначение операционной системы
- •27. Основные функции операционных систем
- •28. Прикладное по
- •29. Язык программирования Паскаль. Общая характеристика. Основные правила записи программ на языке Паскаль. Структура программы. Пример программы
- •6.Понятие типа данных в Турбо Паскаль
- •Простые типы данных
- •Численные (арифметические) выражения
- •Логические выражения
- •Символьные выражения
- •Составной оператор
- •30. Основные элементы языка Pascal
- •31. Понятие типа данных в Турбо Паскаль
- •Простые типы данных
- •Численные (арифметические) выражения
- •Логические выражения
- •Составной оператор
- •34. Ввод и вывод данных в Паскале.
- •Рассмотрим, для начала, Вывод данных в Паскале.
- •Рассмотрим, теперь, Ввод данных в Паскале.
- •35. Условные операторы Pascal-Паскаль
- •36. Оператор выбора Паскаля
- •37. Оператор безусловного перехода
- •38. Счетный оператор цикла или оператор цикла с параметром
- •39. Цикл с предпроверкой условия
- •40. Цикл с постпроверкой условия
- •42. Процедуры и функции
- •Описание и вызов процедур и функций
- •43. Процедуры.
- •44. Численное решение систем нелинейных уравнений
- •Методы численного решения уравнений и систем нелинейных уравнений
- •3.1. Решение нелинейных уравнений
- •3.1.2. Методы уточнения корней нелинейных уравнений
- •Тогда .
- •С погрешностью
- •Откуда при
- •Пусть тогда и
- •45. Метод половинного деления.
- •Тогда .
- •С погрешностью
- •46. Метод хорд
- •47. 52. Метод Ньютона (метод касательных)
- •48. Комбинированный метод хорд и касательных для уточнения корней нелинейных уравнений
- •49. 51. Метод простых итераций
- •50. Решение систем линейных алгебраических уравнений методом Гаусса
- •53. Метод прямоугольников
- •Составные квадратурные формулы
- •Составные формулы для равномерных сеток
- •Погрешность метода
- •Пример реализации
- •54. Метод трапеций
- •Составная формула
- •59. Интерполяцио́нный многочле́н Лагра́нжа
- •Определение
- •Применения
- •Случай равномерного распределения узлов интерполяции
- •60. Разделё́нная ра́зность
- •Определение
- •Применение
- •История
49. 51. Метод простых итераций
В ряде случаев весьма удобным приемом уточнения корняуравнения является метод последовательных приближений (метод итераций).
Пусть с точностью
![]() необходимо
найти корень уравненияf(x)=0,
принадлежащий интервалу изоляции[a,b].
Функцияf(x)и ее первая производная непрерывны на
этом отрезке.
необходимо
найти корень уравненияf(x)=0,
принадлежащий интервалу изоляции[a,b].
Функцияf(x)и ее первая производная непрерывны на
этом отрезке.
Для применения этого метода исходное уравнение f(x)=0должно быть приведено к виду
|
|
(4.2) |
В качестве начального приближения 0 выбираем любую точку интервала [a,b].
Далее итерационный процесс поиска корня строится по схеме:
|
|
(4.3) |
В результате итерационный процесс поиска реализуется рекуррентной формулой (4.3). Процесс поиска прекращается, как только выполняется условие
|
|
(4.4) |
или число итераций превысит заданное число N.
Для того, чтобы последовательность х1, х2,…, хnприближалась к искомому корню, необходимо, чтобы выполнялось условие сходимости:
|
|
(4.5) |
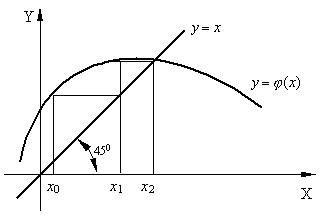
Рис. 4.6. Геометрический смысл метода
Переходим к построению схемы алгоритма
(рис.
4.7). Вычисление функции![]() оформим
в виде подпрограммы.
оформим
в виде подпрограммы.
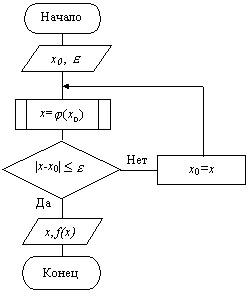
Рис. 4.7. Схема алгоритма уточнения корня методом итераций
50. Решение систем линейных алгебраических уравнений методом Гаусса
Численное
решение систем линейных алгебраических
уравнений с помощью определителей
удобно производить для систем 2-х или
3-х уравнений. Если же число уравнений
больше, то гораздо выгоднее использовать
метод Гаусса. Метод Гаусса заключается
в последовательном исключении
неизвестных.
Пусть необходимо решить
систему:
 где xi
- неизвестные, i = 1, 2, ..., n; n < 200. Если
число уравнений больше, то нужно применять
итерационные методы решения.
ai,j
- элементы расширенной матрицы
коэффициентов
В соответствии с
алгоритмом Гаусса выразим x1
из первого уравнения
(2) x1
= (a1,n+1
- a1,2x2
- ... - a1nxn)/a11
Если
a1,1=0,
то необходимо переставить уравнения
системы. Затем подставим (2) во все
уравнения системы (1), кроме первого.
Таким образом, неизвестное x1
будет исключено из всех уравнений
системы, кроме первого.
При этом
элементы расширенной матрицы преобразуются
по формулам:
a1j(1)
= a1j/a11
aij(1)
= aij
- ai1a1j(1),
i = 2,3,...,n; j = 1, 2, ..., n+1
В результате
исключения x1
из всех уравнений все элементы первого
столбца преобразованной матрицы будут
равны нулю, кроме a11(1)
= 1
Аналогично, x2
выражаем из 2-го уравнения и исключаем
оставшихся уравнений системы и т.д.
В
результате получаем преобразованную
матрицу, у которой все элементы ниже
главной диагонали равны нулю.
Выпишем
соответствующие формулы для исключения
неизвестного xk
и получения коэффициентов преобразованной
матрицы.
где xi
- неизвестные, i = 1, 2, ..., n; n < 200. Если
число уравнений больше, то нужно применять
итерационные методы решения.
ai,j
- элементы расширенной матрицы
коэффициентов
В соответствии с
алгоритмом Гаусса выразим x1
из первого уравнения
(2) x1
= (a1,n+1
- a1,2x2
- ... - a1nxn)/a11
Если
a1,1=0,
то необходимо переставить уравнения
системы. Затем подставим (2) во все
уравнения системы (1), кроме первого.
Таким образом, неизвестное x1
будет исключено из всех уравнений
системы, кроме первого.
При этом
элементы расширенной матрицы преобразуются
по формулам:
a1j(1)
= a1j/a11
aij(1)
= aij
- ai1a1j(1),
i = 2,3,...,n; j = 1, 2, ..., n+1
В результате
исключения x1
из всех уравнений все элементы первого
столбца преобразованной матрицы будут
равны нулю, кроме a11(1)
= 1
Аналогично, x2
выражаем из 2-го уравнения и исключаем
оставшихся уравнений системы и т.д.
В
результате получаем преобразованную
матрицу, у которой все элементы ниже
главной диагонали равны нулю.
Выпишем
соответствующие формулы для исключения
неизвестного xk
и получения коэффициентов преобразованной
матрицы.
 Теперь мы можем определить все
неизвестные xk
последовательно, начиная с xn
и заканчивая x1.
Эта процедура называется обратным ходом
метода Гаусса.
Для того, чтобы уменьшить
погрешность при делении на диагональный
элемент в формуле (3), рекомендуется
осуществлять такую перестановку
уравнений, чтобы поставить на диагональ
наибольший по модулю из всех элементов
рассматриваемого столбца. Модифицированный
таким образом метод Гаусса называется
методом Гаусса с выбором главного
элемента.
Оценить погрешность
численного решения системы можно с
помощью вычисления невязок. Для этого
численные решения xk,
k = 1, 2, ..., n, нужно подставить в систему и
вычислить разность между правыми и
левыми частями уравнений.
Теперь мы можем определить все
неизвестные xk
последовательно, начиная с xn
и заканчивая x1.
Эта процедура называется обратным ходом
метода Гаусса.
Для того, чтобы уменьшить
погрешность при делении на диагональный
элемент в формуле (3), рекомендуется
осуществлять такую перестановку
уравнений, чтобы поставить на диагональ
наибольший по модулю из всех элементов
рассматриваемого столбца. Модифицированный
таким образом метод Гаусса называется
методом Гаусса с выбором главного
элемента.
Оценить погрешность
численного решения системы можно с
помощью вычисления невязок. Для этого
численные решения xk,
k = 1, 2, ..., n, нужно подставить в систему и
вычислить разность между правыми и
левыми частями уравнений.
 При малой погрешности решений величины
невязок rk
будут равны нулю.
При малой погрешности решений величины
невязок rk
будут равны нулю.