§2 Методика формирования представлений о математическом моделировании у учащихся профильной школы

Большие возможности для пропедевтики математического моделирования предоставляются в старших классах. Старшеклассникам следует явно сообщить трехэтапную схему математического моделирования, раскрыть особенности реализации каждого из этапов. [22]

На первом этапе – этапе формализации – осуществляется переход от практической задачи к ее математической модели. Раскрывая сущность первого этапа особенно важно обратить внимание школьников на необходимость выделения существенных факторов, влияющих на изучаемое явление или производственный процесс.

На втором этапе – этапе исследования построенной модели – решается математическая задача, сформулированная на первом этапе. На данном этапе существенны умения перейти от одной математической модели к другой, найти наиболее рациональный метод решения.

На третьем этапе- этапе интерпретации – полученное решение математической задачи переводится на язык исходной практической задачи. Сущность третьего этапа математического моделирования заключается в умении дать верное толкование математического решения задачи, выявить сущность частных решений, найти практические приемы проверки полученного решения, провести исследование найденного результата. [22]

Пример 1. Снаряд пущен с Земли с начальной скоростью v₀=30 м/с под углом α=45º к ее поверхности. Найдите траекторию его движения и расстояние S между начальной и конечной точкой траектории.

Решение. Прежде чем приступить к составлению математической модели данной задачи с учащимися необходимо обсудить, что в процессе решения задачи снаряд следует считать материальной точкой, пренебрегая его размерами.

Этап формализации: Введем систему координат хОу, совместив ее начало О с исходной точкой, из которой пущен снаряд. Ось х направим горизонтально, а ось у- вертикально (рис.3). Из школьного курса физики известно, что движение наряда описывается формулами: , , где t- время, g=10 м/с² – ускорение свободного падения. Выражая t через х из первого уравнения, и подставляя во второе, получим: (3). Уравнение (3) является математической моделью исходной задачи механики.

Рис.3

Этап исследования построенной модели. Построенная кривая (парабола) пересекает ось х в двух точках х₁=0 (начало траектории) и х₂=S= (место падения снаряда). Подставляя в полученные формулы значения v₀ и α, получим y= x-90x², отсюда x=0 и x= 90.

Этап интерпретации результатов. По условию задачи необходимо было найти расстояние между начальной и конечной точкой траектории движения снаряда, то S=90 м, а траектория движения снаряда описывается уравнением y= x-90x².

Для приведенной задачи можно предложить учащимся исследовать зависимость изменения траектории движения снаряда от начальной скорости и угла под которым он будет пущен с Земли.

Пример 2. Найдите высоту конуса наибольшего объема, который можно вписать в шар радиуса 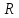(рис.4).

Решение.

Этап формализации. Обозначим через - радиус основания конуса, а через- высоту конуса, тогда. Продлимдо пересечения с поверхностью шара в точкеи соединим ее с. Получим- прямоугольный, т.к.- опирается на, значит. Отсюда , тогда(1). Выражение (1) является математической моделью приведенной геометрической задачи.

Рис.4

Этап исследования построенной модели. Область определения функции V, D(V): h<2R. Найдем производную функции V:

V’=0.

или 4R-3h=0

h=0 h=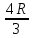

Рис.5

Так как, на заданном промежутке функция непрерывна и имеет на нем один экстремум- точка максимума, то в этой точке она принимаем наибольшее значение.

Этап интерпретации результатов. Исходя из найденного решения делаем вывод, что высота конуса наибольшего объема равна .

При обучении математике в профильной школе, особенного в классах естественнонаучного профиля, следует рассматривать производственные задачи и применяемые для их решения математические методы. Для ознакомления учащихся с сущностью таких методов целесообразно использовать элективные курсы и внеурочные занятия по математике. [24]

Наиболее распространенным методом, особенно в экономике, является метод линейного программирования. Суть этого метода заключается в нахождении экстремальных значений некоторой функции, которая называется целевой, при соблюдении ряда условий, представляющих собой систему линейных уравнений или неравенств, число которых превосходит число переменных. Решать задачи с применением метода линейного программирования можно как аналитически, так и графически.

Пример 3. Сельскохозяйственное товарищество занимается возделыванием только двух зерновых культур- зерновых и картофеля и располагает следующими ресурсами: пашня- 5 000 га, ручной труд- 300 000 человеко- часов и возможный объем тракторных работ- 28 000 условных га. Цель производства- получение наибольшего объема валовой продукции (в стоимостном выражении). Следует найти оптимальное сочетание посевных площадей культур, выращиваемых товариществом.

Решение:

Этап формализации: для составления математической модели воспользуемся нормативами затрат для данного товарищества.

Культура	Затраты на 1 га посева			Стоимость валовой продукции 1 га, усл. ед.
	Ручного труда, человеко- часов	Тракторных работ, условных га
Зерновые	30	4	400
Картофель	150	12	1 000

Таблица 2

Критерием оптимальности является наибольшее значение стоимости валовой продукции. Для поиска оптимального решения обозначим через х₁ га площадь, отводимую под зерновые, а через х₂ га площадь, отводимую под картофель.

Тогда стоимость зерновых составит 400х₁ условных единиц, а стоимость картофеля 1000х₂ условных единиц. Следовательно, общая стоимость валовой продукции составит (400х₁+1000х₂) условных единиц. Обозначим эту сумм через у и назовем полученное выражение у=400х₁+1000х₂ (1) целевой функцией. Необходимо найти наибольшее значений данной функции при соблюдении следующих условий:

1. Общая площадь зерновых и картофеля не должна превосходить 5 000 га, т.е. ; (2)

2. Общие затраты ручного труда не должны превосходить 300 000 человеко- часов, т.е. ; (3)

3. Общий объем механизированных работ не должен превосходить 28 000 условных га, т.е. ; (4)

4. Площади, отводимые под зерновые и картофель, могут принимать только неотрицательные значения, т.е. ,

Таким образом, условие задачи выражается следующей системой неравенств:(5). Требуется найти такие значения, при которых целевая функция у=400х₁+1000х₂ (1) принимает наибольшее значение, удовлетворяющее системе неравенств (5). Уравнение (1) – математическая модель приведенной задачи, которую необходимо исследовать на оптимальность.

На данном этапе следует обратить внимание школьников на то, что число неравенств в системе (5) превосходит число переменных. Такая ситуация является для учеников практически новой.

Этап исследования построенной модели. Решим задачу графически.

Построим прямую х₁+х₂=5000. Координаты всех точек треугольника LOK удовлетворяют неравенству . Построим прямую. Координаты всех точек треугольника АОС удовлетворяют неравенству Построим прямую . Координаты всех точек треугольника ВOD удовлетворяют неравенству

Неравенствам иудовлетворяют все точки первой четверти координатной плоскости х₁Ох₂. Любая точка многоугольника AEMKO удовлетворяет системе неравенств (5).

Рис.6

Для нахождения наибольшего значения целевой функции найдем ее значения в вершинах многоугольника AEMKO.

Вершина	Координаты вершины	Значение целевой функции, усл. ед.
A	(0; 2 000)	2 000 000
E	(250; 1 500)	2 500 000
M	(4 000; 1 000)	2 600 000
K	(5 000; 0)	2 000 000
O	(0; 0)	0

Таблица 3

Таким образом, наибольшее значение целевой функции достигается в вершине М, что соответствует варианту плана, по которому под зерновые отводится 4 000 га, а под картофель 1 000 га.

Этап интерпретации результатов. Оптимальное сочетание посевных площадей культур, обеспечивающее получение наибольшего объема валовой продукции :зерновые- 4 000 га, картофель- 1 000 га.

Помимо метода линейного программирования в классах естественнонаучного направления и экономического профиля целесообразно знакомить учащихся с применением метода наименьших квадратов для решения нематематических задач, применяемых для прогнозирования процессов, протекающих в разных областях производственной деятельности.[24]

Пример 4. Определите перспективную урожайность сельскохозяйственной культуры.

Такая задача решается в связи с перспективным планированием производства сельскохозяйственной продукции. В основу решения этой задачи положены математико- статистические методы.

Этап формализации. Перспективная урожайность определяется по формуле y=a+bx, (1) где а- свободный член уравнения, b- средняя ежегодная прибавка урожайности, х- число лет с начала отсчета. Числовые значения параметров a и b находятся методом наименьших квадратов решением системы уравнений(2).

Наибольшую методическую трудность представляет раскрытие сущности метода наименьших квадратов. [24] Он состоит в следующем.Из формулы (1) следует, что перспективная урожайность является линейной функцией натурального аргумента х. Ее график- множество дискретных точек прямой, имеющих натуральный абсциссы (рис.7).

Отклонения значений фактической урожайности от расчетной аналитически выражаются следующим образом: y_i-a-bx_i. Сущность метода наименьших квадратов состоит в том, чтобы сумма этих отклонений была наименьшей. Это будет иметь место лишь в том случае, когда частные производные функцииf по a и b равны нулю Действительно,

Рис.7

Не трудно заметить, что мы пришли к системе (2). Нуждается в разъяснении смысл знака суммирования:

Математической моделью рассматриваемой задачи является функция, выраженная формулой (1), причем числовые значения параметров a и b находятся методом наименьших квадратов решением системы (2).

Этап исследования построенной модели. Составим таблицу, в которую введем значения фактической урожайности за несколько лет, предшествующих году, урожайность в который предстоит прогнозировать.

Число лет, хi	Фактическая урожайность в ц/га, yi	xi^2	xiyi
1	10,8	1	10,8
2	16,2	4	32,4
3	15,1	9	45,3
4	13,8	16	55,2
5	19,6	25	98,0
6	20,3	36	121,8

Таблица 4

Подставив в систему уравнений (2) значения n, , ,, придем к системе двух линейных уравнений с переменнымиа и b: (3)

Решив систему (3), получим а=10,28 и b=21,62. По формуле (1) найдем перспективную урожайность: у=10,28+1,62·7=21,62.

Этап интерпретации резальтатов. Итак, перспективная урожайность пшеницы в рассматриваемом сельхозпредприятии на будущий год составляет 21,6 ц/га.

Метод наименьших квадратов может быть использован для решения практических задач, связанных с планированием производства продукции, прогнозированием ее себестоимости.

Включение математического моделирования в учебный процесс позволяет активизировать познавательную деятельность школьников, формировать научное мировоззрение учащихся, приобщать их к научному стилю мышления, формировать вычислительные умения и навыки.