
- •К у р с о в а я р а б о т а
- •Глава 1. Теоретическое значение функций нескольких переменных
- •1. Основные теоретические сведения о функциях нескольких переменных
- •2. Значение функций нескольких переменных в прикладной математике
- •3. Значение функций нескольких переменных в экономических областях
- •4. Значение функций нескольких переменных в других областях
- •Глава 2. Практическое значение функций нескольких переменных
- •1.Решение задач с помощью функций нескольких переменных в прикладной математике
- •2.Решение задач с помощью функций нескольких переменных в экономических областях
- •3. Решение задач с помощью функций нескольких переменных в других областях
- •Заключение
- •Список использованной литературы и источников
Глава 2. Практическое значение функций нескольких переменных
1.Решение задач с помощью функций нескольких переменных в прикладной математике
1.Найти
наибольшее и наименьшее значения функции
 в области
в области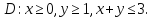
Решение.
Находим критические точки функции
внутри области из условия
 Получаем
Получаем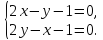 ⇒
⇒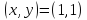 –
точка лежит на границе области
–
точка лежит на границе области
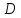 . Значит, внутри области критических
точек нет.
. Значит, внутри области критических
точек нет.
Исследуем
на границе области
 .
Для исследования разбиваем границу на
три участка (соответственно сторонам
треугольника):
.
Для исследования разбиваем границу на
три участка (соответственно сторонам
треугольника):

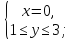

На
первом участке функция имеет вид
 Находим критические точки из условия
Находим критические точки из условия (принадлежит первому участку); тогда
(принадлежит первому участку); тогда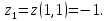
На
втором участке функция имеет вид
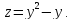 Находим критические точки:
Находим критические точки: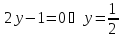 (не принадлежит второму участку).
(не принадлежит второму участку).
На
третьем участке функция имеет вид
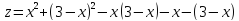 или
или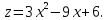 Находим критические точки:
Находим критические точки: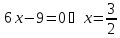 (принадлежит третьему участку); тогда
(принадлежит третьему участку); тогда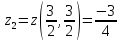 .
.
Вычисляем
значения функции в точках стыка участков
(вершины треугольника):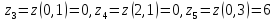 .
Выбираем из полученных значений
наибольшее и наименьшее:
.
Выбираем из полученных значений
наибольшее и наименьшее: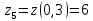 – наибольшее значение,
– наибольшее значение, – наименьшее значение.
– наименьшее значение.
2.Определить,
каковы размеры открытой прямоугольной
ванны данной вместимости
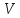 , если она имеет наименьшую площадь
поверхности.
, если она имеет наименьшую площадь
поверхности.
Решение.
Ванна имеет форму прямоугольного
параллелепипеда. Обозначим его размеры
через
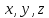 (длина, ширина, высота). Так как объем
(длина, ширина, высота). Так как объем задан, то
задан, то .
Площадь поверхности ванны:
.
Площадь поверхности ванны: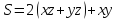 .
Подставляем значение
.
Подставляем значение и получаем функцию двух переменных:
и получаем функцию двух переменных: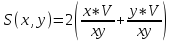 .
Нужно найти точку минимума полученной
функции, причем по смыслу задачи
.
Нужно найти точку минимума полученной
функции, причем по смыслу задачи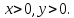
Находим
критические точки, используя необходимое
условие экстремума:
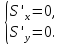 В нашем случае
В нашем случае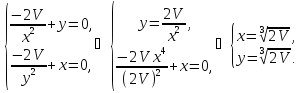 Вычисляем вторые производные и находим
значение дифференциала второго порядка
в критической точке:
Вычисляем вторые производные и находим
значение дифференциала второго порядка
в критической точке:

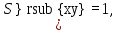
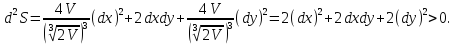 Значит, функция
Значит, функция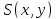 имеет минимум при
имеет минимум при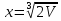 .
Тогда
.
Тогда .
.
2.Решение задач с помощью функций нескольких переменных в экономических областях
Задача 1.Прибыль от производства разных видов продукции
Рассмотрим
типичную задачу нахождения экстремума
функции нескольких переменных, возникающую
в экономике. Пусть
 -
количество производимых
-
количество производимых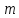 разновидностей продукции, а их цены –
соответственно
разновидностей продукции, а их цены –
соответственно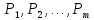 (все
(все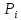 -
постоянные величины). Пусть затраты на
производство этих видов продукции
задаются функцией издержек
-
постоянные величины). Пусть затраты на
производство этих видов продукции
задаются функцией издержек
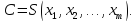
Тогда функция прибыли имеет вид
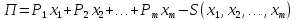
Максимум
прибыли естественно искать как условие
локального экстремума функции многих
переменных при
 (при отсутствии других ограничений)
(при отсутствии других ограничений)

Это
условие приводит к системе алгебраических
уравнений относительно переменных
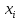
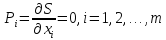
Эта
система уравнений реализует известное
правило экономики: предельная стоимость
продукции равна предельным издержкам
на производство этой продукции. Решениями
этой системы уравнений являются наборы,
состоящие из
 значений каждый. Нужно заметить, что
сам процесс нахождения системы уравнений
зависит от вида функции издержек и может
быть довольно сложным.
значений каждый. Нужно заметить, что
сам процесс нахождения системы уравнений
зависит от вида функции издержек и может
быть довольно сложным.
Пример.
Производится два вида продукции,
обозначим их через
 и
и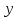 .
Цены этой продукции, соответственно,
.
Цены этой продукции, соответственно,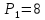 и
и ,
а функция затрат
,
а функция затрат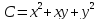 .
Тогда при
.
Тогда при ,
, прибыль является функцией двух переменных:
прибыль является функцией двух переменных:
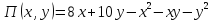
Условия
локального экстремума приводят к системе
линейных алгебраических уравнений
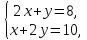 решение которой определяет точку
решение которой определяет точку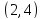 .
Поскольку
.
Поскольку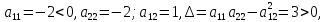 то найденная точка определяет локальный
максимум функции прибыли, который равен
то найденная точка определяет локальный
максимум функции прибыли, который равен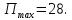
Задача 2.
Потребитель
имеет возможность потратить сумму 1000
денежных единиц на приобретение
 единиц
первого товара и
единиц
первого товара и 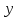 единиц
второго товара. Заданы функция полезности
единиц
второго товара. Заданы функция полезности 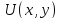 и цены
и цены 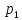 ,
, 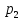 за
единицу соответственно первого и второго
товаров. Найти значения
за
единицу соответственно первого и второго
товаров. Найти значения 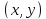 ,
при которых полезность для потребителя
будет наибольшей:
,
при которых полезность для потребителя
будет наибольшей:

Решение.
Рассмотрим
линии уровня функции полезности
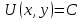 т.е.
т.е.
 .
Используя
свойства логарифмов, имеем:
.
Используя
свойства логарифмов, имеем:
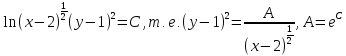
Таким образом, линии уровня представляют собой график функции
 (кривая
безразличия)
(кривая
безразличия)
Легко
видеть, что максимальное значение  ,
а следовательно, и уровня
,
а следовательно, и уровня  достигается
в том случае, если соответствующая
кривая безразличия касается прямой
(линии уровня затрат)
достигается
в том случае, если соответствующая
кривая безразличия касается прямой
(линии уровня затрат)
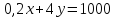 . Так
как градиент в каждой точке перпендикулярен
линии уровня, то из этого следует, что
условие максимальности прибыли может
быть сформулировано следующим образом:
. Так
как градиент в каждой точке перпендикулярен
линии уровня, то из этого следует, что
условие максимальности прибыли может
быть сформулировано следующим образом:
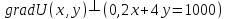
Так
как
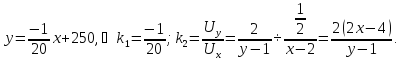
Где
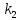 угловой
коэффициент прямой, проходящей через
угловой
коэффициент прямой, проходящей через 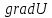 .
.
Из
условия перпендикулярности прямых
имеем 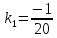 , т.е.
, т.е.
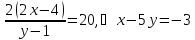 .
Следовательно,
оптимальное распределение потребления
товаров находится как решение системы:
.
Следовательно,
оптимальное распределение потребления
товаров находится как решение системы:
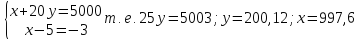
Ответ -
значения, при которых полезность для
потребителя будет наибольшей.
-
значения, при которых полезность для
потребителя будет наибольшей.
