Приставка П.О., Мацуга О.М. Аналіз даних

а

б

Рис. 3.11. Графічне зображення інтервального оцінювання лінійної регресії:

а – N = 30; б – N = 300

Для наочності нижче наведені толерантні межі, довірчі інтервали для лінії регресії та прогнозного значення (рис. 3.12).

Рис. 3.12. Графічне зображення довірчого оцінювання лінійної регресії

Із метою перевірки адекватності відтвореної моделі регресії yˆ (x) = ϕ(x,Θˆ )

висувається статистична гіпотеза Η0 : y (x) = yˆ (x) про вигляд регресійної залежності. Критерій перевірки гіпотези базується на статистиці f:

f= σˆ ε2 , σˆ 2y

яка має F -розподіл Фішера з кількістю степенів вільності ν1 = N −1, ν2 = N − 3. Значення f порівнюють із критичним fα,ν1,ν2 і за виконання нерівності

f ≤ fα,ν1,ν2

роблять висновок про адекватність та значущість відтвореної залежності. Зауваження 3.5. Аналогічна процедура може бути реалізована під час розв’я-

зання задачі про відповідність даним деякої конкретної регресійної моделі (не обов’язково одержаної в результаті відтворення, а, наприклад, суто евристичної).

Як правило, критерій, що враховує конкретний вигляд регресійної залежності yˆ (x) = ϕ(x,Θˆ ), використовують на етапі попередньої ідентифікації моделі

71

регресійної залежності для перевірки гіпотези

ˆ

Η0 : y (x) = ϕ(x;Θ).

Не

зменшуючи загальності,

розглянемо

дані у

вигляді масиву

{xi , yi, j ; i =

, j =

}. У випадку D{y

x} = σ2 = const

для перевірки головної гіпо-

1,k

1,mi

тези реалізується статистична характеристика

k

ˆ

2

ˆ

(N − k)∑mi yi − y (xi;Θ)

f

=

i=1

,

k

mi

)2

(k − s −1)∑∑(yi, j − yi

i=1 j=1

яка має

F -розподіл із кількістю степенів вільності

ν1 = k − s −1,

ν2 = N − k . Якщо

f ≤ fα,ν ,ν

2

, то запропонована регресійна залежність є значуща.

1

Якщо D{y x} = σ2yh2 (x), для перевірки Η0

реалізують статистику

k

ˆ

2

(N − k)∑ωimi

ˆ

yi − y (xi;

Θ)

f ′

=

i=1

,

k

m

(k − s −1)∑ωi ∑i (yi, j − yi )2

i=1 j=1

де

1

ωi = h2 (xi ),

що має F -розподіл із кількістю степенів вільності ν1 = k − s −1, ν2 = N − k . Проце-

дура перевірки гіпотези є еквівалентна вищенаведеній.

Зауваження 3.6. У випадку перевірки гіпотези про лінійний зв’язок s = 2.

До задач лінійного регресійного аналізу обробки даних належить процедура

порівняння двох або більше регресійних залежностей. Слід відзначити, що подібна задача є актуальна, коли з однієї генеральної сукупності одержані різні вибі-

рки.		Отже, нехай			за	вибірковими		даними	Ω2,N = {x1,l , y1,l ;l =		},
										1, N1
									1
Ω2,N		= {x2,l , y2,l ;l =		} відтворені лінії регресії:
	2		1, N2
		ˆ		ˆ	ˆ		ˆ	ˆ	ˆ
					+ b1(x − x1),				+ b2 (x − x2 ),
		y1 (x) = a1					y2 (x) = a2

залишкова дисперсія для яких відповідно визначається так:

							N
	S1,Зал2 =				1		∑1 (y1,l − aˆ1 − bˆ1	(x1,l − x1))2 ,
			N		− 2
				1			l=1
							N
	S2,Зал2 =			1		∑2 (y2,l − aˆ2 − bˆ2			(x2,l − x2 ))2 .
		N		2	− 2
							l=1

Необхідно оцінити, чи істотна різниця поміж yˆ1 (x) і yˆ2 (x).

72

Процедура перевірки гіпотези

Η0 : y1 (x) = y2 (x)

має розбиття на декілька етапів:

1. Спочатку перевіряється гіпотеза про збіг залишкових дисперсій, отже, про рівність дисперсій залишків:

		Η		0	: σ2	= σ2		.
					1,ε		2,ε
Перевірка здійснюється з урахуванням статистичної характеристики
	S2
		1,Зал	,		якщо		S2		> S2		,
	S2,Зал2						1,Зал		2,Зал
f
	=
	S2,Зал2		,		якщо		S2		< S2		,
	2
							1,Зал		2,Зал
	S1,Зал
яка має розподіл Фішера	зі степенями					вільності ν1				= N1 − 2, ν2 = N2 − 2 . У разі

f ≤ fα,ν1,ν2 головна гіпотеза правильна, при цьому обчислюється зведена оцінка дисперсії залишків:

S2 = (N1 − 2)S1,Зал2 + (N2 − 2)S2,Зал2 .

N1 + N2 − 4

2. У випадку рівності залишкових дисперсій реалізується обчислювальна схема перевірки гіпотези

Η0 :b = bˆ1 = bˆ2

на основі статистичної характеристики

				bˆ	− bˆ
t =				1		2						,	(3.6)
	S			1		+		1
			(N1	−1)σˆ 2x			(N2	−1)σˆ	2x
					1				2

де σˆ 2x1 , σˆ 2x2 – незсунені оцінки дисперсій x1, x2 .

Статистична характеристика (3.6) має t -розподіл із ν = N1 + N2 − 4 степенями

вільності, тоді:

1) якщо t ≤ tα 2,ν , то гіпотеза Η0 правильна, таким чином, регресійні прямі є

паралельні, а лінії регресії можуть збігатись або різнитися постійними коефіцієнтами aˆ1, aˆ2 ;

2) при t > tα 2,ν гіпотеза Η0 повинна бути відкинута, отже, регресійні прямі мають різні кути нахилу.

У разі прийняття Η0 обчислюється bˆ1 = bˆ2 = bˆ :

bˆ = (N1 −1)σˆ 2x1bˆ12 + (N2 −1)σˆ 2x2 bˆ22 . (N1 −1)σˆ 2x1 + (N2 −1)σˆ 2x2

73

3. На завершальному етапі перевіряється

Η0 : a = aˆ1 = aˆ2

на основі статистичної характеристики

bˆ

− bˆ

t =

0

,

(3.7)

S0

де

bˆ

=

y1 − y2

;

0

x

− x

1

2

S02

= S2

1

1

1

1

+

+

.

(N1

−1)σˆ

2x

+

(N2 −1)

(x

− x

)2

N1

σˆ 2x

N2

1

2

1

2

Статистична характеристика (3.7) має t -розподіл з ν = N1 + N2 − 4 степенями вільності, тому якщо t ≤ tα 2,ν , то обидві регресійні прямі вважаються ідентичними, у противному разі має місце статистично значущий незбіг.

Якщо дисперсії залишків S1,Зал2 , S2,Зал2 різняться істотно, а отже, гіпотеза про рівність дисперсій залишків не підтверджується, то для порівняння регресійних прямих yˆ1 (x), yˆ2 (x) адекватних статистичних критеріїв не існує. У цьому випадку

рекомендується застосовувати процедуру порівняння регресій на основі наближених формул шляхом перевірки двох гіпотез. Аналогічно попередньому алгоритму

перевіряється гіпотеза

Η

0

:b = bˆ

= bˆ

з урахуванням статистичної характеристики

1

2

bˆ

− bˆ

t =

1

2

,

S2

S

2

S

1,Зал

+

2,Зал

N σˆ 2

N

2

σˆ

2

1

x

x

1

2

яка має t -розподіл із кількістю степенів вільності

2

(1− C0 )

2

−1

ν =

C0

+

,

N

−

2

N

− 2

1

2

де

S2

S2

S2

1,Зал

1,Зал

2,Зал

;

[ ]

– ціла частина.

C =

σˆ 2

σˆ 2

+

σˆ 2

0

N

N

N

2

1

x1

1

x1

x2

Якщо t ≤ tα 2,ν , то правильна гіпотеза про збіг кутових коефіцієнтів ліній

регресій.

Нижчерозглянута процедура полягає в перевірці гіпотези Η0 : a = aˆ1 = aˆ2 на основі статистичної характеристики

	bˆ − bˆ
u =	0	,	(3.8)
	S10

74

де

N σˆ

2

N

2

σˆ

2

N σˆ

2

N

2

σˆ

2

y − y

ˆ

ˆ

1

x

ˆ

x

1

x

x

ˆ

2

1

2

1

2

;

1

;

b

=

b1

+ b2

+

b0

=

S2

S

2

S2

S

2

x − x

1,Зал

2,Зал

1,Зал

2,Зал

1

2

S

2

=

N

S

2

+ N S2

S2

S2

.

2 1,Зал

1

2,Зал +

1,Зал

2,Зал

10

N1N2 (x1 − x2 )2

N1σˆ 2x1 S2,Зал2

+ N2σˆ 2x2 S1,Зал2

Статистична характеристика (3.8) має нормальний розподіл, тому Η0 правильна, коли u ≤ uα 2 . Якщо дві наведені гіпотези правильні, робиться висновок про

їх випадкову різницю, у противному разі має місце істотна розбіжність поміж

yˆ1(x) і yˆ2 (x).

3.3.2.Нелінійний регресійний аналіз

Убагатьох випадках у процесі ідентифікації кореляційного поля виявляється, що треба відтворювати нелінійну регресійну залежність. При цьому підбір кривої може бути здійснений на основі:

1) поліноміальної регресії другого (рис. 3.13):

	y (x) = a + bx + cx2			(3.9)
або більш високого порядку:
y (x) = a	+ a x + a x2		+…+ a xk , k ≥ 3;	(3.10)
0	1	2	k

2) нелінійних залежностей як відносно параметрів, так і відносно аргументів лінії регресії. Цей тип поділяється на регресії:

–ті, що зводяться до лінійної форми відносно параметрів (квазілінійні функції);

–нелінійні функції відносно параметрів, які не зводяться до лінійної форми.

Рис. 3.13. Графік поліноміальної регресійної залежності другого порядку

Для нелінійних функцій, що зводяться до лінійної форми відносно оцінок параметрів, реалізуються різні перетворення координат (логарифмування, заміна змінних та ін.). Після переформування масиву даних до них можна застосувати

75

МНК. Регресії, що характеризуються нелінійністю за оцінюваними параметрами зводяться до нелінійних рівнянь, одержаних за МНК, і для їх відтворення застосовуються ітераційні методи або методи апроксимації параметрів. Ортодоксальної теорії нелінійної регресії не існує. Проте зведення до лінійної форми відносно шуканих параметрів дозволяє реалізовувати статистичні критерії лінійної регресії.

Відтворення параболічної регресії

Безпосереднє застосування обчислювальної схеми МНК до регресійної залежності (3.9) не відрізняється від лінійної. Для залежності (3.10) обчислювальний процес відтворення емпіричної лінії регресії ускладнюється.

Обчислювальні процедури, що ґрунтуються на МНК, вводяться для регресії (3.9), яку подають у вигляді

y (x) = a1 + b1ϕ1 (x)+ c1ϕ2 (x),

(3.11)

де

ϕ1 (x) = x − x ;

	N	N
ϕ2 (x) = x2 −	∑xl3	− x∑xl2
	l=1	l=1
	N

∑xl2 − Nx2

l=1

	1	N		3	− x		2	x
(x − x )+		∑xl2 = x2 −	x						(x − x )− x2 .
					σ2x
	N l=1

Нижче наведені процедури відтворення залежностей (3.9), (3.11) на основі масиву даних {xl , yl ;l =1, N}.

Реалізуючи МНК, з умови

2

1

N

ˆ

2

2

min SЗал 1

= min

∑(yl − aˆ

− bxl − cxˆ l )

,

N − 3

aˆ,bˆ,cˆ

( )

aˆ,bˆ,cˆ

l=1

еквівалентної

∂SЗал2 (1)

= 0,

∂SЗал2

(1)

= 0,

∂SЗал2 (1)

= 0,

∂aˆ

∂bˆ

∂cˆ

одержують

aˆ = y − bˆx − cxˆ 2 ,

де bˆ, cˆ отримують із системи рівнянь

N

N

N

bˆ∑(xl − x )2 + cˆ∑(xl2 − x2 )(xl − x ) = ∑(yl − y)(xl − x ),

l=1

l=1

l=1

N

N

N

bˆ∑(xl2 − x2 )(xl − x )+ cˆ∑(xl2 − x2 )2 = ∑(yl − y)

(xl2 − x2 ).

l=1

l=1

l=1

Ця система є еквівалентна такій:

76

ϕ22 (x)

σˆ 2x

(x3 − x2x )

rˆ

σˆ

σˆ

(x

3

2

x )

− x

bˆ

x,y

x

y

=

,

(3.12)

− (x

)

4

2

2

x

cˆ

(y − y)(x2 − x2 )

де

			1	N
	xk =			∑xik , k =1,2,3,4 ;
			N
				i=1

(y − y)(x2 − x2 )= 1 ∑N (xl2 − x2 )(yl − y). N l=1

Із розв’язку системи (3.12) знаходять оцінки параметрів регресії bˆ, cˆ :

ˆ		(			)	2		(					)	(		)
	x4 − x2						rˆx,yσˆ xσˆ y − x3 − x2x							(y − y) x2 − x2

b =																								,
							(			)		2		(							)	2
														− x3			− x2x
			σˆ 2x x4 − x2
		σˆ 2x										− (				−			x )rˆx,yσˆ xσˆ y
			(y − y)(x2 −								)
									x2						x3		x2						.
	cˆ =
						(				)		2		(							)	2
														− x3			− x2x
			σˆ 2x x4 − x2

Наведені вирази і визначають обчислювальну процедуру відтворення параболічної регресії у вигляді (3.9).

Найпростіша обчислювальна схема відтворення поліноміальної регресії ґрунтується на ортогональних поліномах Чебишева, окремим випадком якої є залежність (3.11). З умови

1

N

2

min

S2

=

min

∑(

y − aˆ

− bˆ ϕ

(

x

− cˆ ϕ

(

x

N − 3

aˆ

,bˆ

,cˆ

Зал(2)

aˆ

,bˆ

,cˆ

l

1

1 1

l )

1 2

l ))

1

1

1

1

1

1

l=1

знаходять оцінки параметрів:

aˆ1 = 1 ∑N yl = y , N l=1

N

∑(xl − x ) yl

bˆ1 = l=N1

∑(xl − x )2

l=1

N

∑ϕ2 (xl ) yl

cˆ1 = l=1N

∑ϕ22 (xl ) l=1

=	(x − x ) y		,	(3.13)
	σˆ	2
		x

= ϕ2 (x) y .

77

З аналізу формули (3.13) випливає, що оцінки aˆ1, bˆ1 повністю збігаються з

оцінками для лінійної регресії у вигляді

y (x) = a + b(x − x ),

що визначається властивостями поліномів Чебишева. Іншими словами, підвищуючи степінь полінома, для кожної приєднаної функції ϕk (x) обчислюють коефіцієнт

регресії, зберігаючи одержані раніше параметри.

Оцінка точності та значущості параметрів aˆ1, bˆ1, cˆ1, як і для лінійної регресії, проводиться шляхом перевірки гіпотез

Η

0

: a = aˆ ,

Η

0

:b = bˆ ,

Η

0

:c = cˆ

1

1

1

1

1

1

на основі статистик

aˆ1 − a1

ta =

N ,

1

SЗал(2)

ˆ

N

=

bˆ1 − b1

∑ϕ12 (xl ) =

(b1 − b1)σx

,

(3.14)

tb

N

SЗал(2)

1

l=1

SЗал(2)

(cˆ1 − c1)

cˆ1 − c1

N

tc

=

∑ϕ22

(xl ) =

Nϕ22 (x) .

SЗал(2)

SЗал(2)

1

l=1

Значущість оцінок параметрів перевіряють, вважаючи a1 = 0, b1 = 0, c1 = 0, на

основі умови ta1 ≤ tα2,ν , tb1 ≤ tα2,ν , tc1 ≤ tα2,ν . Якщо хоча б одна з нерівностей по-

рушується, говорять про «втрату» відповідного члена параболи.

З урахуванням статистичних характеристик (3.14) проводять інтервальне оцінювання відповідних коефіцієнтів регресії:

a

= aˆ

t

α 2,ν

SЗал(2)

,

н,в

1

N

b

= bˆ

t

SЗал(2)

,

н,в

1

α 2,ν σx

N

с

= cˆ

t

SЗал(2)

.

α

2,ν

н,в

1

Nϕ22

(x)

Відхилення окремих значень від оцінки параболічної регресії (рис. 3.14) оцінюється за аналогією з лінійною регресією шляхом призначення толерантних інтервалів, межі яких визначають зі співвідношень

yˆmin (x) = aˆ1 + bˆ1ϕ1 (x)+ сˆ1ϕ2 (x)− tα2,νSЗал(2) , yˆmax (x) = aˆ1 + bˆ1ϕ1 (x)+ сˆ1ϕ2 (x)+ tα2,νSЗал(2) ,

78

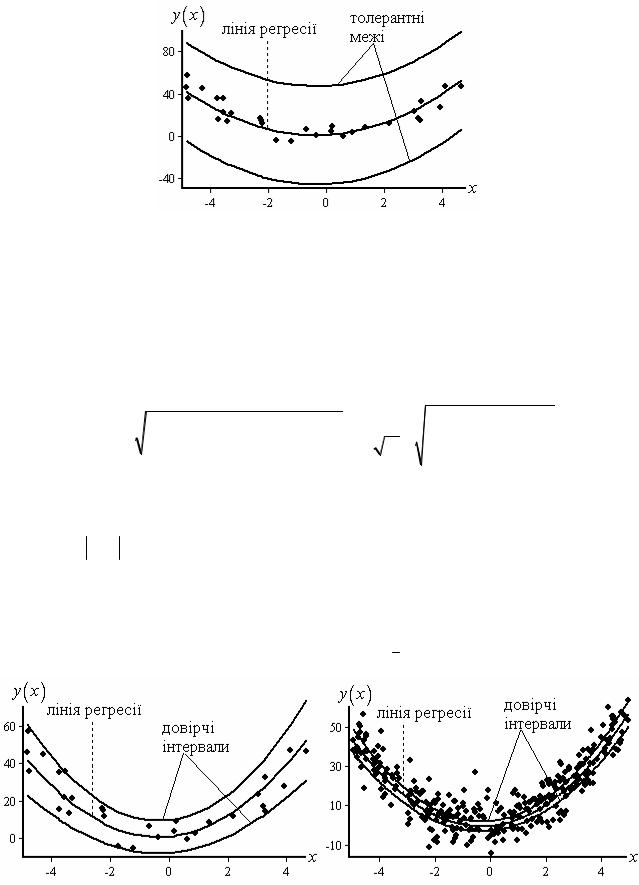
Рис. 3.14. Графічне зображення толерантних меж для параболічної регресії

Відхилення оцінки регресії yˆ (x) від теоретичної оцінюють на основі статистичної характеристики

ˆ

(x)

t(x) =

y (x)− y

,

S(

|x)

y

де (за повною аналогією з лінійною моделлю)

SЗал(2)

ϕ12 (x)

ϕ22 (x)

1

ˆ 2

2

2

2

2

S(

|x) =

σε

+ Sb1

ϕ1

(x)+ Sc1

ϕ2 (x) =

1+

+

;

σ2x

y

N

N

ϕ22 (x)

σˆ 2 = S2

;

S2

=

SЗал2 (2)

;

S2

=

S

Зал2 (2)

.

ε

Зал(2)

b1

Nσ2x

c1

Nϕ22 (x)

Якщо t(x) ≤ tα2,ν , де ν = N − 3, то правильна гіпотеза

Η0 : y (x) = yˆ (x)

іпроводиться інтервальне оцінювання параболічної регресії (рис. 3.15). Межі довірчого інтервалу визначаються так:

yˆн,в (x) = yˆ (x) tα2,νS( y|x) .

а

б

Рис. 3.15. Графічне зображення інтервального оцінювання параболічної регресії:

а – N = 30; б – N = 300

79

Порівняльний аналіз наведених меж із довірчими межами лінійної моделі показує, що чим вищий порядок регресійної кривої, тим більше розходження довірчих меж за віддалення від середнього x .

Побудова довірчого інтервалу для прогнозу нового спостереження здійснюється з урахуванням величини S( y|x0 ) стандартної похибки y при заданому x0:

					= σˆ			2
S	(							ε	1
		y	x
			0 )
				=		SЗал(2)
							N

1

2

2

2

2

+

+ Sb

ϕ1

(x)+ Sc

ϕ2

(x) =

N

1

1

N +1

+

ϕ12

(x)

+

ϕ22 (x)

.

σ2x

ϕ22 (x)

Відповідний довірчий інтервал для нового спостереження y при заданому x0 (рис. 3.16) такий:

yˆ (x0 )− tα2,νS( y|x0 ) ≤ y ≤ yˆ (x0 )+ tα2,νS( y|x0 ) , ν = N − 3.

Рис. 3.16. Графічне зображення довірчого інтервалу для прогнозу нового спостереження у випадку параболічної регресії

Нижче для наочності показані толерантні межі, довірчі інтервали для лінії регресії та прогнозного значення (рис. 3.17).

Рис. 3.17. Графічне зображення довірчого оцінювання параболічної регресії

80