Sopromat

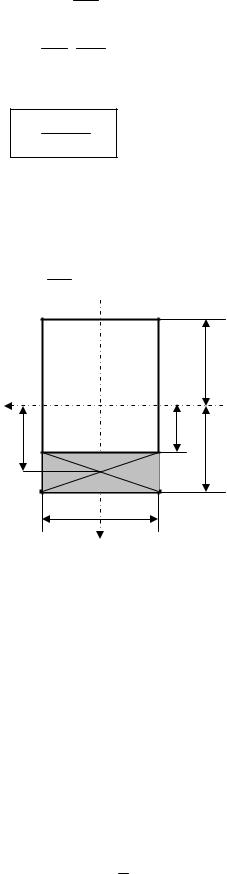
	τ bdx =					dM S		відр			(8.25)
						Iy
або	τ =			dM		Sвідр	.				(8.26)
				dx		Iyb
Використовуючи (8.5), остаточно
	τ =			Q Sвідр				.			(8.27)
				b Iy
Цей вираз називають формулою Журавського.
Цікаво подивитися на розподіл τ по висоті перерізу.
Для прямокутного перерізу (рис. 8.21) знайдемо τ									на відстані	z	від нейтральної осі
y .
Для цього випадку	I	y	= bh3			;
				12
									h/2
	Y
								z
	z1
									h/2
							b
							Z
Рис.8.21. „Відрізана” частина перерізу

або

Тоді

																		h
																						+ z											2
		= F z = b											h							2								b
S	відр														− z										=						h
			1		1								2									2			2							4
				bh2							2z2
S		=					1	−							.
	відр												2
			8								h
			bh2							4z2
		Q			1−							2																	2
			8								h							3		Q						4z
τ =																	=						1	−						.
								3																			2
							bh																			h
				b														2 bh
							12

− z2

(8.28)

Цей вираз вказує на параболічний характер зміни дотичних напружень по висоті перерізу. Неважко помітити, що τ = 0 при z = ± h2 на верхньому та нижньому шарах балки, тобто в тій зоні, де нормальні напруження σ досягають max значень. І навпаки,

101

τ

= 3

Q

(8.29)

max

2 bh

при z = 0 . Тобто, на нейтральній осі, де нормальні напруження σ дорівнюють нулю.

Розподіл по висоті перерізу величин σ

і τ зображено на рис. 8.22.

М

σmax

Q

τmax

z

σ(z)

σmax

σ

τ

Рис.8.22. Розподіл нормальних та дотичних напружень по висоті перерізу

З (8.29) очевидно, що максимальне значення τ більше від того, що було б отримане за розрахунками на звичайний зсув в 1,5 раза.

Тепер можна записати умову міцності для дотичних напружень:

		τ		=	QmaxSвідр max	≤ [τ ]	.	(8.30)
			max		bmin Iy
	Для підбирання розмірів	перерізу одразу за дотичними напруженнями треба було б
	одночасно визначити три величини, пов’язані					між собою – b ;		Iy та Sвідр max , що є

неможливим. Тому на практиці спочатку підбирають розміри перерізу з умови міцності за нормальними напруженнями, а далі перевіряють їх за формулою (8.30). Якщо результати розрахунків задовольняють (8.30), розрахунок закінчують. Якщо ні, то збільшують переріз (вибирають більший розмір сортаменту) і так до тих пір, доки умова не буде виконана. Зрозуміло, що умова міцності за нормальними напруженнями при цьому буде виконуватися автоматично.

102

Лекція 14. Продовження теми 8 (Згин)

Повна перевірка балки на міцність. Згин тонкостінних стержнів.

8.7. Повна перевірка балки на міцність

Як правило, при звичайних інженерних розрахунках можна обмежитися використанням умови міцності за нормальними напруженнями (8.19) та перевіркою міцності за дотичними напруженнями (8.30). Але при розрахунках відповідальних елементів конструкції слід ретельніше дослідити напружений стан, що виникає в балці.

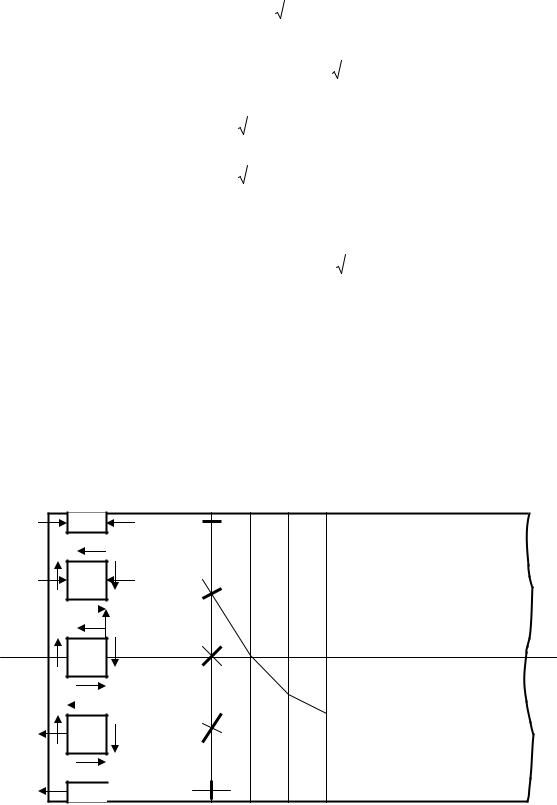
Розглянемо елементи, які знаходяться на різних рівнях перерізу навантаженої балки (рис. 8.23).

					а	σmax
					τmax
		σ1	σ3	τ	в
		д	σ	г	σ
		σ3	σ1	τ	б
					σmax
		Рис.8.23. Складний напружений стан при згині
Елементи „ а ” та „ б ”, вирізані			у крайніх	шарах балки, знаходяться під впливом
максимальних нормальних напружень, а дотичні напруження по їх гранях дорівнюють нулю.
Елемент „ в ” розташований на нейтральній осі навпаки знаходиться під дією τ , а нормальні
напруження відсутні. Розглядаючи елемент „ г ”, можна стверджувати, що на його гранях
будуть діяти і нормальні, і дотичні напруження, причому, якщо на цьому шарі вирізати
елемент за головними площадками, то він буде орієнтований як елемент „д ”.
Виходячи з вищенаведеного, можна зробити висновок, що матеріал балки
знаходиться у неоднорідному складному напруженому стані. Можна стверджувати, що,
перевіряючи на міцність зони, найвіддаленіші від нейтральної осі, треба використовувати
критерій міцності за нормальними напруженнями. Розглядаючи нейтральний шар, перевірку
треба здійснювати за дотичними напруженнями, а при вивченні напруженого стану
проміжних шарів треба використовувати певні теорії міцності.
Взагалі задачу розрахунку на міцність при цьому розбивають на кілька стадій:
1.	Знаходять небезпечний переріз (може статися, що треба буде перевірити кілька
перерізів, в яких виникають Mmax або Qmax				, або і	M і Q приймають одночасно
досить великі значення).
2.	У перерізі знаходять небезпечні точки (шари), в яких приймають великі значення
σ ,	τ	або обидва ці напруження (таких		точок теж може бути кілька).Головні
напруження в кожній точці перерізу в даному випадку визначають за							формулами:

			= 1 [σ +					];
	σ	1				σ 2 + 4τ 2
				2
								.	(8.31)
	σ		=	0;
		2
	σ	3	=	1	[σ − σ 2		+ 4τ 2	]
				3

103

Підставляючи ці вирази у критерій міцності відповідних теорій міцності, отримаємо розрахункові напруження для I,II,III,IV теорій:

= 1

[σ +

]≤ [σ ]

σ

ч

σ 2

+ 4τ 2

.

(8.32)

I

2

1− µ

1+ µ

≤ [σ ]

σ

ч

II

=

σ +

σ 2 + 4τ 2

.

(8.33)

2

2

≤ [σ ]

.

σ

ч

III

=

σ 2 + 4τ 2

(8.34)

≤ [σ ]

.

σ

ч

IV

=

σ 2 + 3τ 2

(8.35)

Аналогічно запишемо вираз для критерію Мора:

1− m

1+ m

≤ [σ ]

σ

ч

=

σ +

σ 2 + 4τ 2

,

(8.36)

M

2

2

[σ

]

де

m = [σ+

].

−

Практика показала, що для розрахунку балок із пластичних матеріалів доцільно використовувати III та IV теорію міцності.

Цікавим є не тільки визначення величин головних напружень, але й їх орієнтації в різних шарах балки. Це потрібно, наприклад, при розгляді питання про конструювання залізобетонних балок.

Розглянемо напрямки головних напружень у різних точках якогось перерізу (рис. 8.24). Тонкими лініями показано напрямок σ1 , товстими – σ3 .

1
2	2
3	2/

2//

2///

4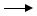

5

Рис.8.24. Траєкторії головних напружень

104

Траєкторії головних напружень (ізостати) можна побудувати, проводячи з точки, де відомі напрямки σ1 та σ3 , відрізок до перетину з наступним перерізом за

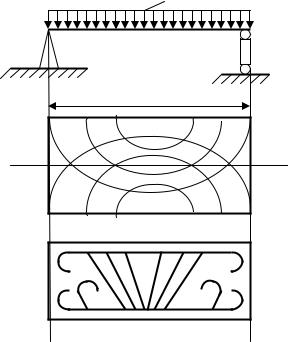
напрямом того напруження, траєкторію якого будуємо. З отриманої точки знов треба провести відрізок до перетину із наступним перерізом, орієнтуючи цей відрізок за напрямком напруження вже в даній точці, й т.д. При досить малій відстані між перерізами ця ламана лінія перетвориться у криву, яку називають ізостатою або траєкторією головного напруження. В залізобетонних балках арматуру потрібно розташовувати за напрямом траєкторії головних розтягуючих напружень (рис. 8.25).

q

l

а)

б)

Рис.8.25. Принцип армування залізобетонних балок:

а) картина ізостат; б) розташування арматури

8.8. Згин тонкостінних стержнів

Ми вже розглядали питання про дотичні напруження, що виникають при згині. Слід відзначити, що за умови врахування дотичних напружень при згині, треба відкинути гіпотезу плоских перерізів.

Якщо тонкостінний переріз завантажується у площині симетрії, для нього діють формули, виведені у гл.8.

Розглянемо питання про розподіл дотичних напружень у випадку навантаження перерізу не у площині симетрії. Покажемо існування осі, паралельної до осі стержня, коли сили, які діють у будь-якій площині, що проходить через цю вісь, не викликають кручення. Точку перетину цієї осі з площиною перерізу (т. C на рис. 8.26) назвемо центром згину.

Якщо це так, то сума моментів усіх дотичних сил у перерізі відносно т. C дорівнює 0. На елемент ds з координатами x, y діє сила τδds (δ – товщина стержня). Тоді її

момент відносно т. C буде

τ δ ds p ,

де p – довжина перпендикуляра, опущеного з т. С на дотичну. Якщо С є центром згину, то

h

∫τδpds = 0 .

0

105

У

С

Р

Х

dS

Рис. 8.26. Центр згину

p ds – це подвоєна площа трикутника з основою ds та вершиною в т. С. Нехай pds = dω ,

h

dω

то

∫τδ

ds = 0 .

0

ds

Проінтегрувавши за частинами, отримаємо:

τδω

0h −

h

∂(τδ )

∫

ds

ωds = 0 .

0

δ = 0 якщо s = 0 або s = h.

Перетворюючи, отримаємо

Qy

h

Q

h

∫ yωδds +

x

∫xωδds = 0 ,

I

I

x

0

y

0

а, так як Qx та Qy – довільні, положення центра ваги визначимо такими умовами:

h

Iωx = ∫ yωδds = 0;

0

(8.37)

h

Iωy = ∫xωδds = 0 .

0

Дуже просто знайти центр згину для кутникового профілю (рис. 8.27). Якщо

С

Рис. 8.27. Кутниковий профіль

вершину С прийняти за полюс, то секторіальна площа ω = 0 . Тому умови (8.37) виконуються і вершина кута С є центром згину.

106

Лекція 15. Тема 9. Деформації та переміщення при згині

Деформації та переміщення, що розглядаються при згині. Аналітичні методи визначення деформацій та переміщень при згині. Диференціальне рівняння зігнутої осі балки. Приклади інтегрування наближеного рівняння зігнутої осі балки.

9.1. Деформації та переміщення, які розглядають при згині

Під деформаціями (а точніше переміщеннями) при згині розуміють прогин та кут повороту перерізу (рис. 9.1).

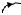
Θ F

f

Рис.9.1. Прогин - f та кут повороту - Θ при згині

Позначимо прогин – f , а кут повороту −θ . Через те, що кут θ дуже малий, можна записати

	tgθ =θ =	dy	,	(9.1)
		dx

тобто функція кутів повороту θ є першою похідною від функції прогинів по довжині балки.

Існують різні теоретичні методи визначення переміщень при згині:

-аналітичні, що базуються на інтегруванні наближеного диференціального рівняння зігнутої осі балки;

-графічні й графоаналітичні, які засновані на зв’язку аналітичних виразів та графічних зображень – епюр внутрішніх силових факторів;

- енергетичні, що створені при розгляді зв’язку деформацій та рівнем потенціальної енергії, яка при цьому накопичується в об’єкті, й т.п.

9.2. Аналітичні методи визначення деформацій та переміщень при згині. Диференціальне рівняння зігнутої осі балки

Нехтуючи впливом на кривизну балки перерізуючої сили

1

=

M (х)

,

ρ(x)

EI(х)

де ρ(x) – радіус кривизни шару.

З курсу математики відомо

d2 y

1

= ±

dx

2

.

ρ(x)

3

1+

dy

2

2

dx

Q , можна записати:

(9.2)

(9.3)

107

EI(х)

Порівняємо праві частини формул (9.2) та (9.3). Вважаючи, що при додатному моментові M додатною є й кривизна, а при від’ємному − кривизна теж буде від’ємною, у формулі можна залишити тільки знак „ + ”:

		d 2 y
										M (х)
		dx2							=		(9.4)
						3				EI(х)
1+	dy			2		2
	dx

(якби вісь y була направлена вниз, частини рівняння були б протилежні за знаком). Це рівняння зігнутої осі балки. Враховуючи, що маємо справу з малими деформаціями і

величина dy dx

зігнутої осі

або

значно менша від 1, можна записати

d 2 y = M (х) dx2

d 2 y

EI(х) dx2 = M (х) .

наближене диференціальне рівняння

(9.5)

(9.6)

Використовуючи ці співвідношення, а також (9.1), можна визначити прогини та кути повороту перерізів балки.

Інтегруючи (9.4) один раз, матимемо

dy

=θ (x) = ∫

M (х)

dx + C

.

(9.7)

dx

EI(х)

Інтегруючи цей вираз ще раз, отримаємо

y(x) = ∫dx∫

M (х)

dx + Cx + D .

(9.8)

EI(х)

Вирази (9.7) та (9.8) мають дві константи інтегрування C та

D , які знаходимо з

граничних умов.

При цьому зрозуміло, що:

-D – не що інше, як збільшений в ЕІ разів прогин на початку координат, тобто, D = EI y(0);

-С – не що інше, як збільшений в ЕІ разів кут повороту на початку

координат, тобто, C = EI θ (0) .

9.3.Приклади інтегрування наближеного рівняння зігнутої осі балки

1.Розглянемо балку, навантажену зосередженою силою, як зображено на рис.9.2., та знайдемо прогин і кут повороту перерізу на кінці консолі в т.В. Виберемо початок правосторонньої декартової системи координат у жорсткому защемленні (т.А) і будемо вважати жорсткість балки ЕІ величиною постійною.

Тоді, записуючи вираз М(х) справа від перерізу, матимемо

М(х)= - F(l-x)

і наближене рівняння зігнутої осі балки буде мати вигляд

108

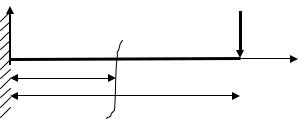
	EIy// (x) = −F (l − x) .
	Y		F
		X
А	х		В
	l

Рис.9.2. Консольна балка, навантажена на вільному кінці зосередженою силою

Відповідно після інтегрування матимемо

	EIy/ (x) = θ (x) = −Flx +					Fx2	+ C ;
						2
	EIy(x) = −Fl	x2	+	Fx3	+ Cx + D .
				6
	2

Визначимо константи інтегрування C та D з граничних умов. У даному випадку вони будуть виглядати так

	у(0)=0	та				θ (0)=0 ,
звідки стає зрозумілим, що	C=D=0 .
Тоді
	EIy/ (x) = θ (x) = −Flx +					Fx2
						2
і відповідно
	EIy(x) = −Fl	x2	+	Fx3	.
		2		6

Тоді кут повороту і прогин в т.В будуть відповідно дорівнювати:

θ

= θ (l) =

1

(−Fl 2 +

1

Fl

2 ) = −

Fl

2

;

B

EI

2

2EI

.

(9.9)

y

= y(l) =

1

(−

1

Fl

3

+

1

Fl3 ) = −

Fl

3

;

B

EI

2

6

3EI

Знаки “ - “ у відповідях вказують на орієнтацію переміщень у вибраній правосторонній системі координат – прогин спрямований донизу, а кут повороту – за годинниковою стрілкою.

2.Розглянемо балку, навантажену рівномірно розподіленим навантаженням, як зображено на рис.9.3, та знайдемо прогин і кут повороту перерізу на кінці консолі в т.В. Але цього разу виберемо вже лівосторонню систему координат із початком на кінці консолі в т.В.

109

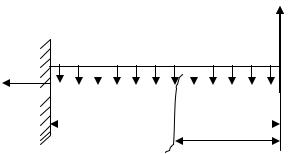
Y

X

А В

l

x

Рис.9.2. Консольна балка, навантажена розподіленим навантаженням

Тоді, записуючи вираз М(х) справа від перерізу, матимемо:

М(х)= - qx2/2

і наближене рівняння зігнутої осі балки буде мати вигляд:

EIy

// (x) = −

qx2

.

2

Відповідно після інтегрування, матимемо:

EIy/ (x) = θ (x) = −

qx3

+ C

;

6

EIy(x) = −

qx4

+ Cx + D .

24

Визначимо константи інтегрування C та D

з

граничних умов. В даному

випадку вони будуть виглядати так:

у(l)=0

та

θ (l)=0 ,

звідки стає зрозумілим, що

C =

ql3

та

D = −

ql 4

.

6

8

Тоді

EIy/ (x) = θ (x) = −

qx3

+

ql3

6

6

і відповідно

EIy(x) = −

qx4

+

ql3

x −

ql 4

.

24

6

8

Тоді кут повороту і прогин в т.В будуть відповідно дорівнювати:

θ

= θ (0) =

ql 3

та

y

= y(0) = −

ql 4

.

(9.10)

B

6EI

B

8EI

Знак “ - “ у відповіді для прогину вказує на орієнтацію переміщень у вибраній лівосторонній системі координат – прогин спрямований донизу, а кут повороту – додатний і орієнтований за годинниковою стрілкою.

Лекція 16. Продовження теми 9 (Деформації та переміщення

110