Sopromat

Лекція 8. Продовження теми 6 (ГХПП)

Головні осі інерції. Головні моменти інерції. Еліпс інерції. Обчислення моментів інерції та опору для деяких характерних перерізів. Визначення моментів інерції, опору та інших геометричних характеристик для прокатних профілів (двотаври, швелери, кутники тощо).

6.2.3. Головні осі інерції. Головні моменти інерції.

Цікавим є питання про визначення осей, відносно яких моменти інерції будуть набувати найбільшого та найменшого значення. Позначимо ці осі „u” та „v”. Дослідимо на екстремум вираз (6.18). Взявши першу похідну та прирівнявши її до нуля, матимемо

− 2 cos α sin α Ι x + 2 sin α cos α Ι y − 2 cos 2α Ι xy = 0

або, перетворюючи

	Ιx − Ιy	sin 2α + Ιxy cos2α = Ιx y = 0 .		(6.22)
	2
		1	1

Тобто, Ιx1 та Ιy1 приймають екстремальні значення відносно тієї пари осей, для яких відцентровий момент Ιx1 y1 = 0. Тобто, за прийнятими нами позначеннями головних осей

індексами „u” та „v” можна записати Ιuv = 0 . Нехай Ιu = Ιmax , а Ιv = Ιmin (це відбувається за тієї умови, що Ιx > Ιy ).

Головними осями інерції називають осі, відносно яких відцентровий момент дорівнює

нулю.

Відносно головних осей виникають екстремальні значення моментів інерції, які теж

називають головними моментами інерції.

Площини, проведені через вісь стержня та головні осі інерції називають головними

площинами інерції.

Цікавим є визначення орієнтації головних осей та значень головних моментів інерції. Нехай у перерізі є довільні взаємно перпендикулярні осі х та у. Відомі моменти інерції відносно цих осей Ιx ,Ιy та Ιxy . Потрібно встановити орієнтацію головних осей u та

v, тобто визначити кут повороту на головні осі α0 і визначити головні моменти інерції Ιu та

Ιv .

Для визначення орієнтації головних осей розглянемо вираз (6.20). Для головних осей відцентровий момент дорівнює нулю, тому

Ιx

− Ιy

sin 2α

+ Ι

cos2α

= 0

0

xy

0

2

або

tg 2α 0 = −

2 Ι xy

,

(6.23)

Ι x − Ι y

1

2Ιxy

звідки

α

=

arctg

−

.

(6.24)

2

Ι

− Ι

0

x

y

61

Для визначення головних моментів розглянемо формули (6.18 – 6.19)

Ι

u

= Ι

x

cos2 α

0

+ Ι

y

sin2 α

0

− Ι

xy

sin 2α

0

;

Ι

v

= Ι

x

sin2 α

0

+ Ι

y

cos2 α

0

+ Ι

xy

sin 2α

0

.

Розглянемо суму цих величин та їх різницю:

Ιu + Ιv = Ιx + Ι2 ;

(6.25)

Ιu − Ιv = Ιx cos2α0 − Ι y cos2α0 − 2Ιxy sin 2α =

= (Ιx − Ι y )cos2α0 + (Ιx

− Ι y )tg2α0 sin 2α0

= (Ιx

− Ι y )

Тоді з (6.25) та (6.26)

1

1

Ιu

=

Ιx + Ι y + (Ιx

− Ι y )

;

2

cos2α

1

1

Ιv

=

Ιx

+ Ι y − (Ιx

− Ιy )

.

2

cos2α

Або, зробивши заміну

1

4Ι2

= ± 1+ tg2

2α =

1+

xy

,

cos2α

(Ι

x

− Ι

y

)2

отримаємо:

1

[Ι

]

Ι

=

+ Ι

+ (Ι

− Ι

)2 + 4Ι

2

u

2

x

y

x

y

xy

1

[Ι

]

Ι

=

+ Ι

− (Ι

− Ι

)2 + 4Ι

2

v

2

x

y

x

y

xy

1 .(6.26) cos2α0

(6.27)

(6.28)

.(6.29)

Таким чином, отримано можливість визначати як положення (орієнтації) головних осей, так і значень головних моментів інерції перерізу.

6.2.4. Еліпс інерції.

Вище вже згадувалося поняття радіусів інерції i

=

Ι

x

;

i

=

Ιy

.

x

A

y

A

Головним осям u та v відповідають головні радіуси інерції i

=

Ιu

;

i =

Ιv

.

u

A

v

A

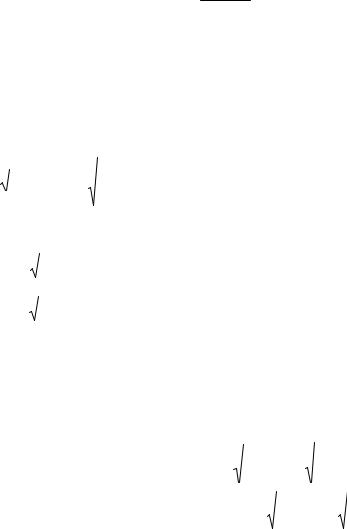
На головних центральних осях інерції перерізу можна побудувати еліпс із півосями, що дорівнюють головним радіусам інерції, причому вздовж осі u відкладемо iv , а вздовж осі

v − iu (рис. 6.5).

Цей еліпс називають центральним еліпсом інерції. Він має цікаву властивість – радіус інерції відносно будь-якої центральної осі Z визначається як перпендикуляр ОA, проведений з центра еліпса до дотичної, яка паралельна даній осі (у нашому випадку осі Z). Точку дотику легко отримати побудовою хорди, яка проходить паралельно осі Z. Промінь, проведений з центра еліпса через середину цієї хорди, пройде через точку дотику на кривій еліпса. Після

цього, вимірявши радіус інерції iz - відрізок ОВ, можна отримати момент інерції: Ιz = iz 2 A .

62

V

B

iu Z

CD

A			β
β	iz		iv
		O
			U

					Рис. 6.5. Еліпс інерції
6.3. Обчислення моментів інерції та опору для деяких характерних перерізів
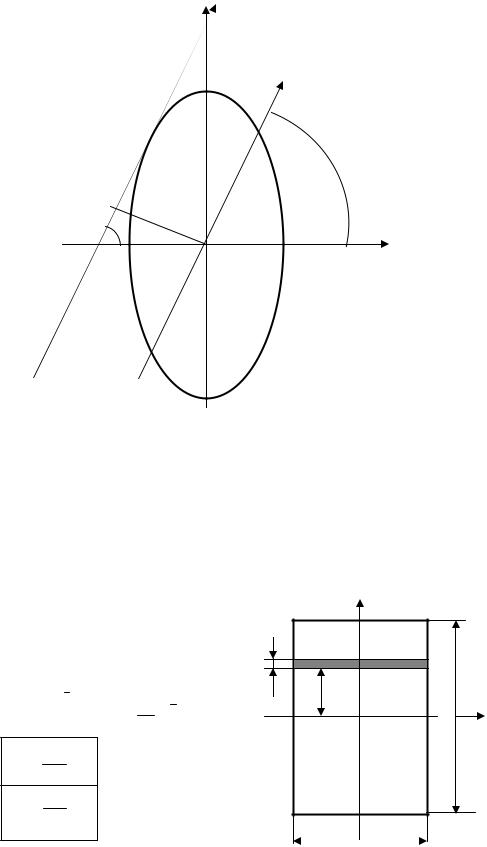
6.3.1.Прямокутник.
Нехай задано прямокутник (рис. 6.6). Обчислимо його осьові моменти інерції Ιx ,Ιy
(Х, У – центральні, головні осі інерції): Ι x = ∫ y2 dA.								У
							A
Елементарну площадку dA можна виразити як
добуток bdy , тоді							dy
				h				у
				2	2bdy = 2 y	3	h
			Ιx	= 2∫ y			b |02	h	X
				0	3
або	Ι	x	= bh3		;		(6.30)
				12
аналогічно	Ι	y	= bh3		.		(6.31)
				12
								b
Обчислюючи осьові моменти опору
Wy та Wz ,				отримаємо:			Рис. 6.6. Прямокутний переріз

63

Ιx

bh3

bh2

W =

=

12

=

;

(6.32)

x

ymax

h

6

2

Ιy

hb3

hb2

W

y

=

=

12

=

.

(6.33)

xmax

b

6

2

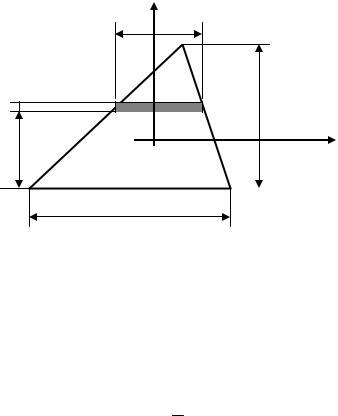
6.3.2. Трикутник.

Нехай задано довільний трикутник (рис. 6.7), вісь Х співпадає з основою, а Х0 −

центральна.

Y

b(y)

dy

C

h

X0

y

X

b

Рис. 6.7. Трикутний переріз

Знайдемо спочатку Ιx :

Ιx = ∫ y2dA.

A

Елементарна площадка dA запишеться як dA = b(y)dy ,

де

тобто,

					h − y
b(y) = b							= b 1
					h
			h		1−	y		dy
Ι		=	∫	by2
	x
			0			h

−y , h

або

Ι

=

bh3

.

(6.34)

x

12

Для центральної осі

x0 момент інерції підрахуємо за допомогою формули

паралельного переносу (6.13), знаючи, що центр ваги трикутника знаходиться на рівні

1

3

висоти від основи.

Ι

= Ι

− a2 A =

bh3

−

h2

bh

.

x

x0

12

9

2

64

Знак „ –„ у формулі вибрано тому, що здійснюється перехід від нецентральної осі до центральної. Тобто,

Ι		=	bh3		.	(6.35)
	x0
		36

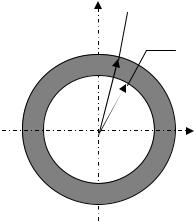
6.3.3. Круг.

Нехай задано круг з радіусом R (рис. 6.8). Знайдемо момент інерції відносно будьякої центральної осі, наприклад, Х:

Ιx

= ∫ y2dA.

A

Площадку dA можна уявити як добуток b(y)dy . З рис.6.8 очевидно, що

b(y) = 2Rsin

α

, а

y = Rcosα . Тоді dy = −

1 Rsin α dα .

2

2

2

2

Отже,

dy

b(y)

Y

0

α

α

1

α

Ιx = ∫R

2

cos

2

2Rsin

Rsin

dα

.

(6.36)

R

2

2

−

2

2

π

Перетворюючи і змінюючи межі інтегрування,

одержимо:

y

α

π

α sin

π

Ιx = R4 ∫cos2

2 α dα = R4 ∫sinαdα .

(6.37)

X

0

2

2

0

Тобто,

Ι

=

πR4

.

(6.38)

x

4

Осьовий момент опору

Рис. 6.8. Круглий переріз

W =

Ι

x

=

πR3

.

(6.39)

x

ymax

4

Скориставшись залежністю між осьовими та полярними моментами інерції та враховуючи, що для круга будь-яка центральна вісь є головною, можна підрахувати полярні моменти інерції та опору:

Ι

= 2Ι

=

πR

4

(6.40)

Р

x

2

W

=

πR3

.

(6.41)

p

2

65

6.3.4. Кільце.	Y R

Нехай задано кільце ( рис. 6.9).

Тоді моменти інерції можна підрахувати за властивостями інтегральних сум.

Тобто,

Ι

=

πR4

−

πr4

x

2

4

або у вигляді

Ι

=

πR4

(1−α 4 )

,

x

2

де

α =

r

.

R

Аналогічно

W =

πR3

(1−α 4 )

;

x

4

Ι

=

πR4

(1−α 4 )

;

p

2

W

=

πR3

(1−α 4 )

.

p

2

r

X

(6.42)

Рис.6.9. Кільцевий переріз

(6.43)

(6.44)

(6.45)

6.4.Визначення моментів інерції, опору та інших геометричних характеристик для прокатних профілів (двотаври, швелери, кутники тощо)

Визначення моментів інерції, опору та інших геометричних характеристик для прокатних профілів (двотаври, швелери, кутники тощо) проводять за допомогою таблиць сортаменту, представлених у різних довідниках, підручниках і задачниках з опору матеріалів і деталей машин.

66

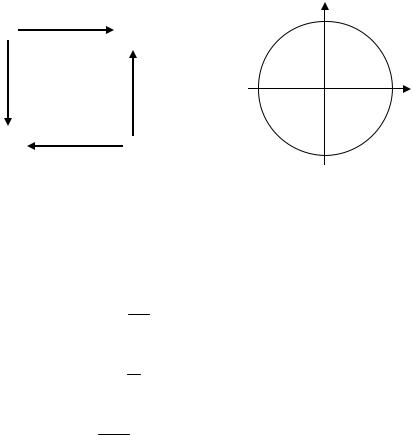
Лекція 9. Тема 7. Чистий зсув. Кручення

Чистий зсув, напруження, умова міцності, приклад розрахунку на міцність заклепкового з'єднання, деформації, з-н Гука при зсуві, модуль пружності ІІ роду. Кручення, внутрішні силові фактори при крученні, напруження, критерій міцності, деформації, закон Гука, умова жорсткості при крученні.

7.1. Чистий зсув, напруження, умова міцності

Чистий зсув (або зріз) – це випадок плоского напруженого стану, коли по

гранях елемента діють тільки дотичні напруження.

У цьому випадку неважко визначити величини та напрямки головних напружень, розглядаючи, наприклад, круг Мора, зображений на рис. 7.1.

			τ
	τ		τ
		σ3	σ1
τ		τ	σ

τ

- τ

Рис.7.1. Напружений стан при чистому зсуві

Тоді цілком зрозуміло, що

σ1 = −σ 3 = τ;

σ2 = 0.

Якщо згадати, що τ = dQ та врахувати, що дотичні сили dA

однакові по кожній площадці dA, то можна записати

τ = Q

A

Очевидно, що умовою міцності при цьому буде

τ max = Qmax ≤ [τ ].

A

(7.1)

dQ, які викликають зсув,

(7.2)

(7.3)

7.1.1. Приклад розрахунку на міцність заклепкового з'єднання.

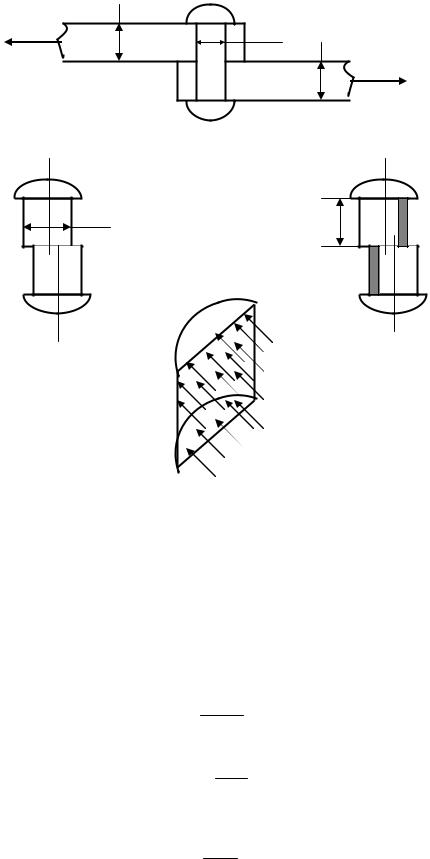
Як правило, деформація зсуву зустрічається у сукупності з іншими видами деформації. Характерний приклад – робота найпростішого заклепкового з’єднання (рис. 7.2) .

Нехай задача полягає в тому, щоб розрахувати кількість заклепок n у ряді, які з’єднують між собою дві пластини товщиною t , що розтягуються силами F . При цьому діаметр заклепки d , допустимі напруження на зріз −[τ ] та на зминання (стиск) − [σ ].

Заклепка одночасно працює і в умовах зсуву (по діаметральному зрізу на границі дотикання пластин однієї до другої (рис. 7.3а) та зминання (по площадках контакту заклепки з кожною пластиною (рис 7.3б,в).

67

	t
F	d
	t
	F

Рис.7.2. Заклепкове з΄єднання

d

t

a)

б)

в)

Рис.7.3. Навантаження на різні зони заклепки: а) зона зсуву, б) зона зминання; в) ефективне навантаження

Тоді розрахунком на міцність при зрізі буде

τ max =			F			≥ [τ ],
	n	/ πd		2
			4

де n/ − кількість заклепок із розрахунку на зріз. Звідси отримаємо

n/ ≥	4F
	πd 2 [τ ] .	(7.4)

Розрахунок на міцність при зминанні дасть

σ max = n//Ftd < [σ ],

де n// − кількість заклепок з розрахунку на зминання. Тобто, за умов міцності на зминання

F
n// ≥ td[σ ]	(7.5)

Очевидно, ці розрахунки можуть дати різні значення n - n/ та n// . З цих двох значень треба буде вибрати найбільше для того, щоб задовольнялися обидві умови міцності − і на зріз, і на зминання.

68

7.2. Деформації, закон Гука при зсуві, модуль пружності ІІ роду

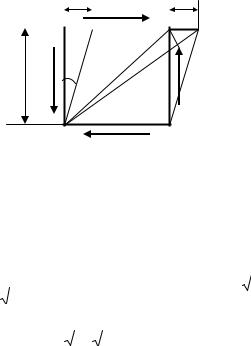
Розглянемо деформацію елемента

ABCD , що знаходиться в умовах чистого зсуву

(рис. 7.4).

За абсолютну

деформацію

при

зсуві приймають

величину

S . За

відносну

деформацію γ ~ tgγ =

S .

Розмірність

величини S −

одиниці

довжини.

Відносна

a

деформація γ − безрозмірна величина.

Розглянемо деформацію видовження діагоналі AC цього елемента.

Δs

Δs

B

τ

C

C /

K

a

τ γ

τ

A

τ

D

Рис.7.4. Деформації при чистому зсуві

Враховуючи, що деформації малі, маємо

ε =

KC′

;

AK

KC′ =

S

;

AK = AC = a 2 .

2

Тоді

ε =

S

=

S = γ .

(7.6)

2a

2

2a

2

Враховуючи (7.6) та закон Гука (5.25), матимемо:

ε =

1

[σ

− µσ

]=

γ

(7.7)

1

3

2

E

або

τ

[1− µ]=

γ .

E

2

Звідки

τ =

Eγ

.

(7.8)

2(1+ µ)

Позначимо

E

= G

.

(7.9)

2(1+ µ)

Тоді (7.4) перетвориться

на

τ = Gγ

або

γ =

τ

.

(7.10)

G

Залежності (7.6) виражають закон Гука

при зсуві. Величину G

називають модулем

Юнга другого роду

або модулем пружності другого роду чи модулем зсуву. Розмірність та

69

фізичний зміст цієї величини аналогічні модулю Юнга першого роду E (при розтягу – стиску).

Залежності (7.8) можна переписати

S = Q a GА

	або	S =	Qa		,	(7.11)
			GA
	де Q − сила, що зсуває площадку площею					A . Величина GA має такий же фізичний

зміст, що й величина EA при розтягу − стиску і називається жорсткістю при зсуві.

7.3. Кручення

Кручення – це вид деформації, який виникає при прикладанні до стержня пар сил, що утворюють моменти в площинах, перпендикулярних до осі стержня.

Стержень, що працює на кручення, називають валом.

На доповнення до основних гіпотез опору матеріалів, що розглядалися раніше, введемо ще дві:

–гіпотеза плоских перерізів: плоскі перерізи, перпендикулярні до осі вала,

залишаються плоскими під час деформації;

–відстань між цими перерізами не змінюється.

7.4.Внутрішній силовий фактор при крученні. Напруження. Умова міцності

Оскільки кручення виникає при прикладанні пар сил у площинах, перпендикулярних до осі стержня, в довільному перерізі з шести можливих внутрішніх силових факторів

виникає тільки один – крутний момент T		(рис. 7.5).
Т			Т

Т

Рис. 7.5. Внутрішній силовий фактор при крученні

Розглянемо напруження, які виникають при крученні круглого вала радіуса r .

З характеру дії внутрішнього силового фактора зрозуміло, що в перерізі, перпендикулярному до осі вала, ці напруження мають дотичний характер.

Розглядаючи елемент вала довжиною dx (рис.7.6) і його переріз, перпендикулярний

до осі, можна записати лише одне рівняння рівноваги, а саме:
T = Tвн = ∫τ ρ ρ dA ,	(7.12)

A

де ρ – відстань від центра перерізу до площадки dA, що розглядається (рис. 7.7); τρ – напруження на цій площадці.

70