Sopromat

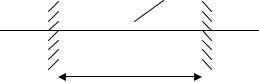
σ		=		N3		=		FE3								(4.10)
	3			A			2E A cos3		α + E					A
													3
		3				1		1						3
та до умов міцності
						FE cos2 α						≤ [σ1 ];
σ1 =						1										(4.11)
			2E			A cos3		α + E	3	A
		1				1				3
σ 3		=					FE3					≤ [σ 3 ].				(4.12)
				2E A cos3				α + E	A
		1				1			3	3

З цих двох виразів отримаємо два значення сили F. Для подальших розрахунків виберемо, безумовно, найменше з цих двох значень сили.

Цікавим буде випадок, коли жорсткість середнього стержня така ж сама, як і жорсткість крайніх стержнів. Тобто E1 = E3 = E , A1 = A3 = A

Тоді формули (4.7) – (4.12) набудуть вигляду

N3

=

F

;

(4.13)

2cos3 α +1

N

=

F cos2 α

;

(4.14)

1

2cos3 α

+1

σ 3

=

F

;

(4.15)

A(2cos3

α +1)

σ1

=

F cos

2 α

.

(4.16)

A(2cos3

α +

1)

Зрозуміло, що в цьому випадку σ

3

≥ σ

1

, тому що cos2 α ≤ 1. Тоді умова міцності буде

виглядати так:

σ max

= σ 3 =

F

≤ [σ ].

(4.17)

A(2cos3

α +1)

Розглянутий метод розрахунку статично невизначених систем називають

розрахунком за допустимими напруженнями.

4.3.Температурні та монтажні напруження

4.3.1.Температурні напруження

Розглянемо стержень, жорстко закріплений з обох кінців (рис. 4.6).

Нехай відомі його механічні параметри: довжина − l ,		А
площа поперечного перерізу − A , модуль Юнга
І роду − E , коефіцієнт лінійного температурного
розширення −αt .
Цей стержень закріплено при температурі t0 ,		l
після чого температура піднялася на t . Треба
розрахувати напруження, які при цьому виникають у	Рис.4.6. Нагрітий стержень

стержні.

Розглянемо сили, які виникають у стержні. Внаслідок температурного впливу стержень намагається розширитися, але це йому не вдається завдяки жорсткому закріпленню кінців (рис. 4.7).

31

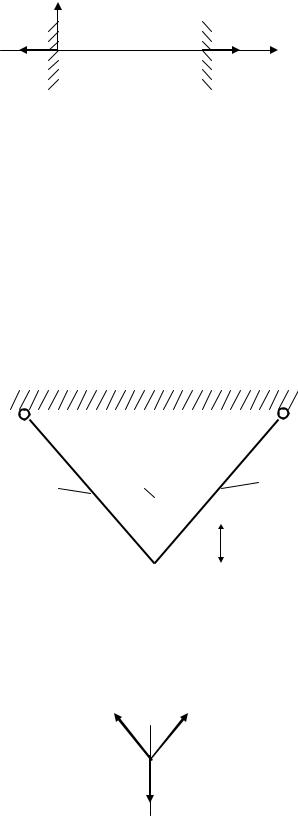
Виникають реакції опор Rл та Rпр .			Y
Розглядаючи рівновагу за допомо-		Rл			R пр X
гою рівнянь статики
∑X = Rл − Rпр = 0,	(4.18)
		Рис.4.7. Сили, що виникають при нагріванні
можна з’ясувати лише, що Rл	= Rпр .

Рівняння статики одне, а невідомих − два.

Система один раз статично невизначена. Складаємо рівняння сумісності деформації,

розглядаючи можливі температурні деформації

l та деформації за рахунок сил Rл та Rпр −

l(R) .

lt

=

l(R)

(4.19)

або

α

t =

Rлl

,

(4.20)

t

EF

тоді

σ =

Rл

= Eα

t .

(4.21)

F

t

Цікавим є те, що напруження в

даному випадку не залежить від довжи-

ни стержня.

4.3.2. Монтажні напруження

1

2

3

Розглянемо систему (рис. 4.8.), в

якій один із елементів зроблено не за

А

розміром (середній стержень коротший,

ніж треба), але всі стержні треба з’єдна-

В

ти в одній точці C (рис. 4.9). Нехай стер-

жні зроблено з одного й того ж матеріалу

і мають однаковий поперечний переріз.

Позначимо крайні стержні 1 та 3,

а середній − 2. Розглядаючи т.С, яка

Рис. 4.8. Система, в якій виникають

лежить між точками А і В і в якій

монтажні напруження

з’єднаються всі три стержні при

монтажі, можна скласти три рівнян-

ня статики:

N1

N3

С

.

N2

∑X = −N1 sinα + N3 sinα = 0

∑Y = N1 cosα + N3 cosα − N2

= 0

(4.22)

Рис. 4.9. Розподіл сил

∑MC = 0

32

Очевидно, що система є один
раз статично невизначеною. Розглянемо
сумісність деформацій стержнів.
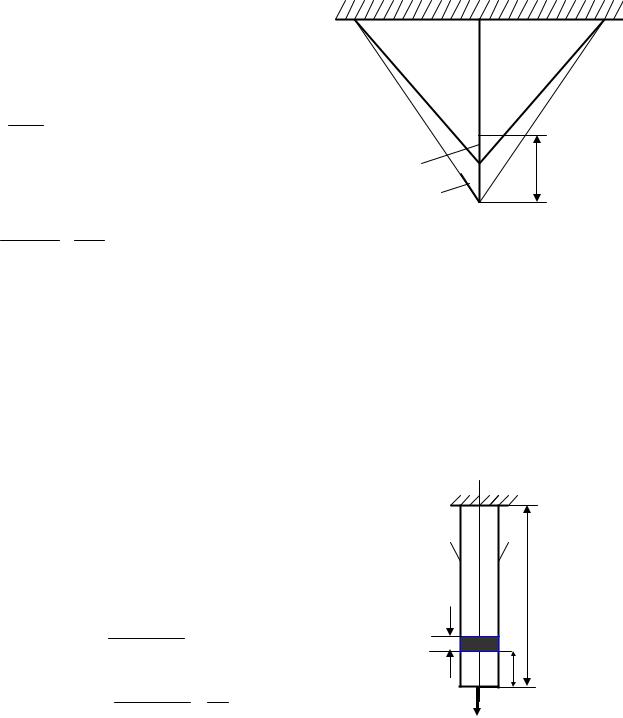
З рис.4.10 випливає, що
l1 +	l	2	= .		(4.23)		А
cosα
Використовуючи закон Гука,						Δl2	С
отримуємо ще одне рівняння						Δl1
							В
N1l1	+ N2l2 =			,	(4.24)	Рис.4.10. Деформації в системі
EF cosα			EF

яке розв’язуватиметься разом із системою (4.22).

Таким чином, можна зробити висновок, що розв’язок наведених задач зводиться до розгляду статично невизначених систем.

4.4.Урахування власної ваги та сил інерції при розтягу–стиску

Убільшості випадків зовнішні навантаження в елементах конструкцій значно перевищують власну вагу самих елементів або сил інерції, що виникають при прискореннях цих елементів. Але бувають випадки, коли цими факторами неможливо нехтувати. Дію власної ваги або сил інерції враховують як розподілене по довжині стержня навантаження.

При врахуванні власної ваги формула (2.1) дещо змінюється. Нехай питома вага

стержня, зображеного на рис. 4.11 − γ .
Тоді нормальна сила в довільному перерізі на
відстані x від вільного кінця стержня
						А	E
N(x) = F + γAx .						(4.25)
Розглянемо видовження короткої ділянки цього							l
стержня довжиною dx :						dx
dx = (F + γAx)dx .						(4.26)
	EA
Інтегруючи, отримаємо							х
x	(F + γAx)dx	=	Fx	+	γAx2	(4.27)	F
x = ∫					.
0	EA		EA		2EA

З цієї формули очевидно, що характер							Рис.4.11. Навантажений стержень
розподілу видовжень при врахуванні власної
ваги є квадратичним на відміну від лінійного
розподілу при врахуванні тільки зовнішніх сил.
Неважко помітити, що видовження стержня довжиною l								буде в цьому випадку
	l =		Fl	+	γAl	2		(4.28)
					2EA
			EA
або	l =		Fl	+	Ql		,	(4.29)
			EA		2EA

33

де Q − власна вага стержня.

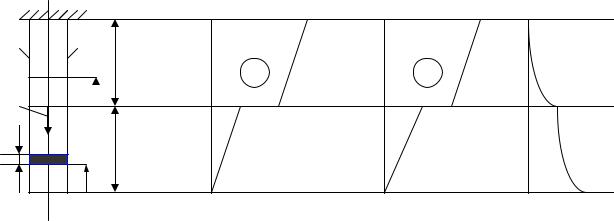
Наприклад: нехай є стержень, навантажений зовнішньою силою F та власною вагою (рис. 4.12 a ). Нехай площа поперечних перерізів всюди однакова й дорівнює A , модуль Юнга І роду − E ; довжини ділянок відповідно −a і b , питома вага −γ .

Запишемо функції розподілу нормальних сил і напружень у довільному перерізі нижньої частини стержня (0 ≤ x < a) :

	N1 (x) = γAx ;					(4.30)
	σ		(x) =	N(x)	= γx .	(4.31)
		1		A

Розглянемо деформацію першої ділянки. Видовження дуже малої ділянки довжиною dx на відстані x від нижнього кінця буде дорівнювати

dx =	N(x)dx	.	(4.32)
	EA

Щоб отримати закон розподілу, треба проінтегрувати цей вираз:

x =	N(x)x	=	γAx	2	.	(4.33)
	2EA
			2EA
	N(a+b)					σ(a+b)

A	E
	b	+	+
F
		N1(a) N2(a)= N1(a)+	σ1(a) σ2(a)
dx	x2	+F
	a
	x1
	N(x)	σ(x)	δ(x)
a)	б)	в)	г)

Рис. 4.12. Стержень, що розтягується з урахуванням власної ваги (а). Розподіл нормальних сил (б), нормальних напружень (в) та переміщень (г)

Повністю на довжині „ a ” стержень буде мати видовження:

a =	N(a)a	=	γAa	2	.	(4.34)
	2EA
			2EA

Перейдемо до другої ділянки(a ≤ x ≤ a + b) і запишемо аналогічні функції. Очевидно

N2 (x) = N(a) + F +γA(x − a) ;						(4.35)
σ 2 =	N2	(x)	=	N(a) + F	+ γ (x − a) ;	(4.36)

AA

34

x		= a +		(N ( a ) + F )( x − a )			+	N ( x − a )( x − a )		=
	2
				EA					2 EA		(4.37)
			(N ( a ) + F )( x − a )			γ	( x −		a ) 2
=		a +			+
							2 E		.
				EA

У даному випадку можна узагальнити, що функції нормальних сил і напружень при врахуванні власної ваги є лінійними, а функції переміщень та видовжень – квадратичними.

Епюри розподілу величини N(x) σ (x) та δ (x) зображені на рис. 4.12б, в, г. Аналогічні висновки можна зробити і для дії сил інерції.

4.5. Розрахунок статично невизначених систем за граничним станом

Тепер, знаючи механічні властивості пластичних матеріалів, можна запропонувати ще один метод розрахунку на міцність статично невизначених систем, які працюють на розтягстиск.

Удеяких випадках при статичному навантаженні системи можна розраховувати за припущенням, що в окремих їх елементах напруження можуть перевищувати допустимі або навіть виходити на рівень границі текучості. Зрозуміло, що при цьому повинна виконуватися умова міцності для всієї конструкції в цілому.

Принцип цього розрахунку полягає в тому, що конструкційні матеріали у більшості випадків є пластичними і мають площадку текучості. Якщо в процесі навантаження в стержнях виникають різні деформації та напруження, що їм відповідають, то можливий варіант, коли при виході напружень у стержнях на рівень текучості вони стануть рівними між собою в той час, як деформації в них будуть різними.

Уцьому випадку зусилля в будь-якому „i ”-ому стержні буде знайдено як

Ni = σi Fi

(4.38)

Тоді ці вирази для Ni можна підставити у рівняння статики, отримавши при їх розв’язанні величину навантаження Qтк − так звану критичну силу, яке вводить усю систему в стан текучості. Так як дію на систему такої сили Qтк , яка б повністю вводила систему в стан текучості, допустити не можна, слід зменшити її значення у „κ ” разів. Тобто

Q		=	Qтк	.	(4.39)
	доп
			κ

Цілком зрозуміло, що застосування методу розрахунку на міцність за допустимими навантаженнями (за граничною вантажопідйомністю) передбачає наявність у деяких елементах системи напружень, що виходять на рівень текучості, і дасть значення сили Qдоп дещо більшим, ніж застосування методу розрахунку за допустимими напруженнями, ідеєю якого є вихід максимальних напружень на рівень допустимих, тобто значно менших від границі текучості

σ		≤ [σ ] ,	де	[σ ] =	σ T	.
	max
					k

35

Лекція 5. Тема 5. Складний напружений стан

Поняття про складний напружений стан. Головні площадки. Головні напруження. Лінійний напружений стан. Напруження на похилих площадках. Плоский напружений стан. Пряма й обернена задачі. Круги Мора. Напруження на октаедричних площадках. Об'ємний напружений стан.

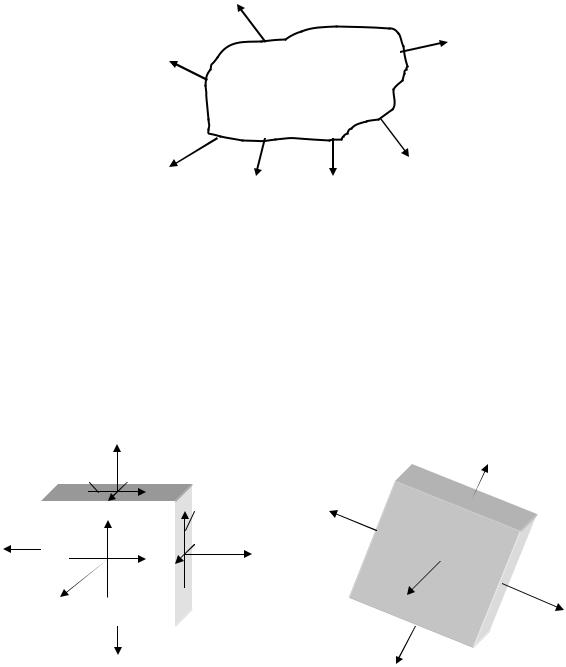
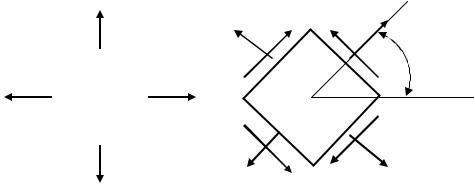
Нехай є навантажене зовнішніми силами Fі тіло (рис. 5.1). Виріжемо в довільній точці цього тіла елементарний об’єм у вигляді кубика, зображеного на рис. 5.2.

	F1
Fі	F2

Fk

F5

F4

F3

Рис. 5.1. Навантажене тіло

По гранях цього кубика в загальному випадку діятимуть 9 компонент напружень. Нормальні σ x ;σ y ;σ z , та дотичні τ xy ;τ xz ;τ yx ;τ yz ;τ zx ;τ xy .

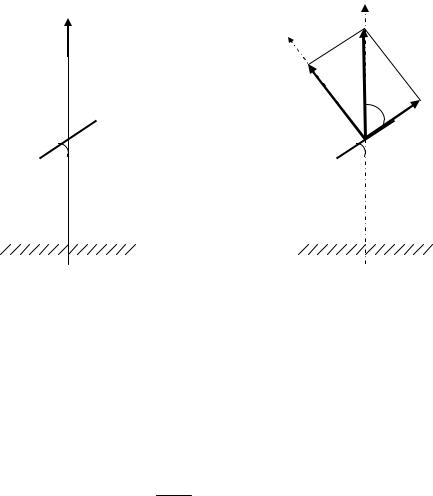
З курсу теорії пружності відомо, що можна вибрати таку орієнтацію граней кубика, що дотичні напруження зникнуть і залишаться тільки нормальні (рис. 5.3).

Площадки, на яких діють тільки нормальні напруження, а дотичні відсутні, називають головними площадками, а відповідні нормальні напруження, що діють по цих площадках називають головними напруженнями. Головні напруження позначають σ1;σ2 ;σ3 . При цьому

прийнято, що σ1 ≥ σ 2 ≥ σ3 (з урахуванням знака).

σz

	τzy	τzx		σ3
			τyz	σ2
		τ xz
σy		τxy	τух σy
	σx			σ1	σ2
		σz
				σ3
Рис. 5.2. Напруження на гранях				Рис. 5.3. Напруження на головних
	кубика в загальному випадку			площадках

Розрізняють три види напруженого стану:

36

− лінійний – коли одне з головних напружень не дорівнює нулю, а два інших дорівнюють нулю. Тут можливі два варіанти – перший, коли σ1 ≠ 0, а σ2 = σ3 = 0, – це одновісний розтяг, і другий, коли σ1 = σ2 = 0, а σ3 ≠ 0, − це одновісний стиск;

−плоский – коли одне з головних напружень дорівнює нулю, а два інших не дорівнюють нулю;

−об’ємний – коли жодне з головних напружень не дорівнює нулю.

5.1.Лінійний напружений стан. Напруження на площадках, розташованих під кутом до осі стержня

Розглянемо напруження, які виникають у розтягнутому стержні на різних площадках (рис. 5.4). Власною вагою стержня в цьому випадку будемо нехтувати.

На площадці, нормальній до осі − A0 , виникають напруження:

σ

=

N

при N = F .

(5.1)

0

A0

F

F

n

pα

σα

α

τα

Аα

Аα

α

α

А0

А0

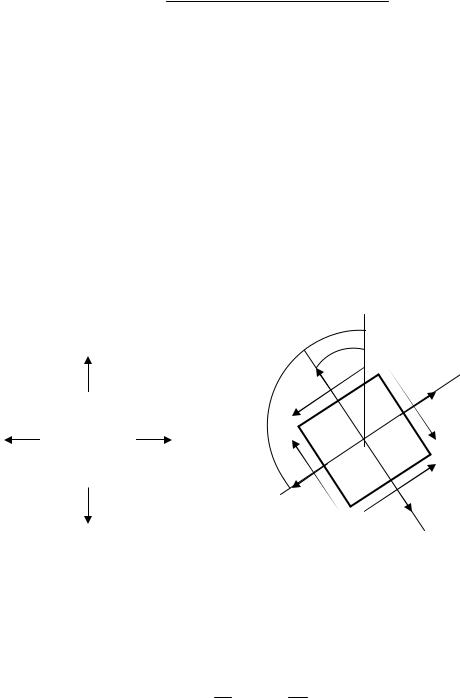
Рис. 5.4. Лінійний напружений стан				Рис. 5.5. Розподіл напружень на
					нахиленій площадці
Тепер розглянемо напруження на площадці Aα , нахиленій під кутом α до площини
A0 (α − кут між нормаллю до площадки Aα			і віссю стержня) (рис 5.5).
Повне напруження на цій площадці
р =	N	=	F	cosα ,	(5.2)
α	Aα		A0

тому що

Aα = cosA0α .

Тоді	pα = σ0 cosα .						(5.3)
Розглядаючи складові, будемо мати
нормальне напруження
	σ	α	= σ	0	cos2	α	(5.4)

37

і дотичне напруження

		τ	α	= σ	0	cosα sinα =	σ0	sin 2α		.	(5.5)
						2

При цьому не важко переконатися, що виконується залежність

p	2	= σ 2	+ τ 2 .	(5.6)
	α	α	α

Слід зауважити: якщо нормальне напруження вважається додатним при розтягу, а від’ємним − при стиску, то дотичне напруження на грані вважається додатним, якщо воно намагається повернути частину елемента, що розглядається, за годинниковою стрілкою.

Від’ємним буде протилежний напрямок.

5.2.Плоский напружений стан

5.2.1.Пряма задача (аналітичне виведення).

Розглянемо елемент у вигляді кубика, „вирізаного” з тіла на головних площадках. Нехай він знаходиться у плоскому напруженому стані (рис. 5.6,а) і головні напруження задані таким чином: σ1 ≠ 0; σ2 ≠ 0; σ3 = 0.

Треба знайти напруження на площадці, повернутої на кут α до тієї головної, де діє σ1 (рис. 5.6б).

	σ1		σα α	τβ
			β=α+900	σβ
			τα
σ2		σ2	τβ
			σβ
	σ1		τα	σα
	а)		б)

Рис. 5.6. Плоский напружений стан: а) головні площадки; б) площадки, розвернуті відносно головних

Розглянемо рис. 5.7.

Використовуючи принцип суперпозиції, на основі (5.4) та (5.5) можна записати

σα = σ1 cos2 α +σ 2 cos2 β;

σσ

τα = 21 sin 2α + 22 sin 2β

або, враховуючи, що β = α + 90O ;

σ

α

= σ

1

cos2

α +σ

2

sin2

α;

(5.7)

τ

α

=

σ1 −σ 2

sin 2α .

(5.8)

2

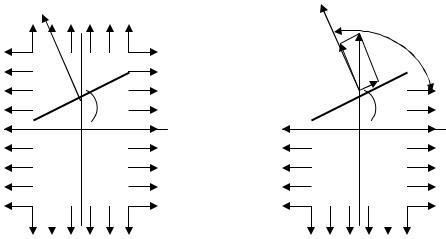
Тепер запишемо напруження, які виникають на площадці, перпендикулярній до нами розглянутої (тобто, розвернутої до тієї головної, де діє σ1 , на кут β (рис. 5.6б та 5.7).

Тоді

σ

β

= σ

1

cos2 (α + 90O )+ σ

2

sin2

(α + 90O )

і

σ

β

= σ

1

sin2 α + σ

2

cos2

α

.

(5.9)

38

n		σ1		n
					σα	pα	β=α+900
						τα
		α				α
σ2			σ2	σ2			σ2

σ1

σ1

Рис. 5.7. Плоский напружений стан. Зміна напружень при повертанні площадок

Аналогічно	τ		=	σ1 −σ 2	sin(α + 90O	),
		β
			2
а	τ	β	= −σ1 −σ2 sin 2α				.	(5.10)
			2
Дослідимо вираз (5.7) на extremum.
(σα )′ = −2σ1 cosα sinα + 2σ2 sinα cosα = −(σ1 −σ2 )sin 2α = 0 .								(5.11)

Звідси випливає, що нормальні напруження досягають max та min значень там, де дотичні дорівнюють 0. Тобто головні напруження є екстремальними.

Відносно τα зрозуміло, що найбільше значення (за модулем) τα отримає, якщо sin 2α = 0 , тобто α = ±45O та кратні їм кути.

τ	max	=	σmax − σmin		.	(5.12)
		2

Складемо почленно (5.7) та (5.9), тоді

σα + σ β = σ1 + σ2	.	(5.13)

Тобто сума нормальних напружень на взаємно перпендикулярних площадках є величиною сталою. Порівнюючи (5.8) та (5.10) неважко помітити, що

τα = −τβ	.	(5.14)

У теорії напруженого стану можна розмежувати дві основні задачі. Перша – пряма задача – коли задано головні напруження і кут повороту площадки, на якій треба визначити напруження σα і τα . Друга – обернена задача – коли задані напруження на неголовних

площадках і треба визначити величини головних напружень та орієнтацію головних

39

площадок. Обидві задачі можна розв’язати як аналітично, так і графічно – за допомогою кругів Мора.

Мор Хрістіан Отто (1835-1918) – німецький учений. Один із засновників графічної кінематики, розробив так званий метод трьох моментів, створив одну з діючих теорій міцності. Розробив метод сил для розкриття статичної невизначеності та узагальнив формули Максвелла (теорема Максвелла – Мора).

5.2.2. Круги Мора (пряма задача)

Круг Мора – це геометричне місце точок (у випадку плоского напруженого стану – коло), координати яких відповідають чисельним значенням нормальних і дотичних

напружень, що діють у точці на площадках, які мають різні кути нахилу.

Тобто круг Мора – це геометрична інтерпретація напруженого стану в певній точці навантаженого твердого тіла.

Нехай задано головні напруження σ1 та σ 2 , а треба знайти напруження на площадках, розвернутих під кутом α до головних площадок (рис. 5.8).

	σ2	σβ	σα
		τβ	τα α
σ1		σ1
		τα	τβ
	σ2	σα	σ β

Рис. 5.8. Плоский напружений стан. Пряма задача

Вибираємо орієнтацію осей σ та τ таким чином, щоб вісь σ співпадала з напрямком більшого з головних напружень. Вісь τ буде спрямована перпендикулярно (рис. 5.9).

Відкладаємо на осі σ значення σ1 та σ 2 (т.т. A та B ). Після цього ділимо відстань

між отриманими точками навпіл і вибираємо цю точку за центр кола, яке базується на відрізку осі AB як на діаметрі.

Як вже було сказано, круг Мора – це геометричне місце точок, координати яких відображають напруження на площадках, нахилених під різними кутами в точці тіла, що досліджується. Тому для того, щоб знайти напруження на площадці, нахиленій до головної під кутом α , слід з центра кола C провести промінь під кутом 2α або з точки на осі σ , що відповідає σmin , провести промінь під кутом α . Перетин цих променів із колом дасть

точку D (рис. 5.9), координати якої будуть відповідати σα та τα .

Дійсно, радіус кола

AC = BC = DC = σ1 −σ2 . 2

40