
- •Скворцова м.И., Мудракова о.А., Кротов г.С.
- •Оглавление
- •Занятие 1. Понятие функции. Основные элементарные функции, их свойства и графики.
- •Обзор основных элементарных функций.
- •Задачи для самостоятельного решения.
- •Занятие 2. Полярная система координат. Построение графиков функций методом сдвига и растяжения вдоль осей координат.
- •Геометрические преобразования графиков функций.
- •I. Случай 1), 2).
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Занятие 5. Точки непрерывности и точки разрыва функции. Классификация точек разрыва. Исследование функции на непрерывность.
- •Классификация точек разрыва
- •Геометрическая иллюстрация этих определений:
- •Задачи для самостоятельного решения
- •Занятие 6. Контрольная работа №1 по теме "Вычисление пределов функций. Исследование функции на непрерывность". (Вариант – образец.)
- •Скворцова Мария Ивановна
Занятие 2. Полярная система координат. Построение графиков функций методом сдвига и растяжения вдоль осей координат.
Определение. Основные элементыполярной системы координат–
полярная ось и полюс. По отношению к ним
определяется положение точки на
плоскости.Полярные координатыточки![]() – это пара чисел
– это пара чисел![]() ,
где
,
где![]() – расстояние от
– расстояние от![]() до полюса
до полюса![]() ,
а
,
а![]() – это угол между полярной осью и
– это угол между полярной осью и![]() .
(см. рис.1).
.
(см. рис.1).


Пусть полярная система координат
расположена так, что полюс совпадает с
началом декартовой системы координат,
а полярная ось – с осью
![]() .
Пусть точка
.
Пусть точка![]() имеет декартовы координаты
имеет декартовы координаты![]() и
и![]() ,
т.е.
,
т.е.![]() ,
а полярные –
,
а полярные –![]() и
и![]() ,
т.е., с другой стороны,
,
т.е., с другой стороны,![]() (см. рис.2).
(см. рис.2).
Тогда:
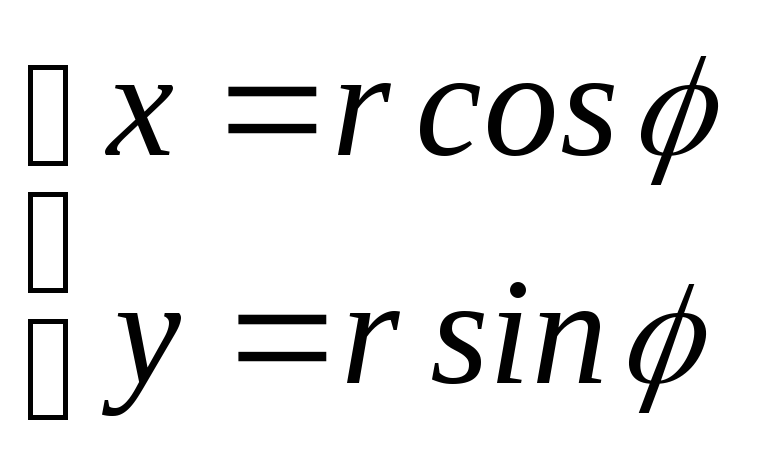 ;
;
Примеры:
Даны декартовы координаты точки
 :
: .
Найти её полярные координаты, т.е.
.
Найти её полярные координаты, т.е.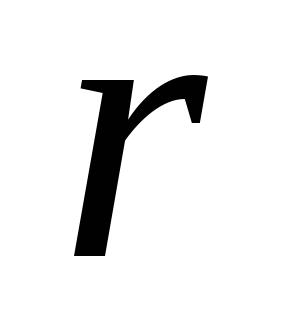 и
и .
.
▲ Имеем:
![]() ,
,![]() ,
,
![]() .
.
Даны полярные координаты точки
 :
: .
Найти её декартовы координаты, т.е.
.
Найти её декартовы координаты, т.е. и
и .
.
▲ Имеем:
![]() ,
,
![]() .
.
Задать кривые в полярных координатах (при помощи уравнения
 ).
).
а)![]() ;б)
;б)![]() ;в)
;в)![]() .
.
▲ Подставим в уравнение кривой вместо
![]() выражение
выражение![]() ,
а вместо
,
а вместо![]() – выражение
– выражение![]() ,
и выразим
,
и выразим![]() через
через![]() :
:
а)![]() ;
;
б)![]() ;
;
в)![]() .
.
Геометрические преобразования графиков функций.
Предположим, построен график функции
![]() .
Требуется построить на его основе график
функции
.
Требуется построить на его основе график
функции![]() ,
где
,
где![]() – константы. Далее, в таблице приведен
ряд правил построения таких графиков.
– константы. Далее, в таблице приведен
ряд правил построения таких графиков.
|
|
Преобразование функции |
Преобразование графика |
|
|
|
График
|
|
|
|
График
|
|
|
|
При
|
|
|
|
При
|
|
|
|
Сохранить
часть графика
|
|
|
|
Сохранить
часть графика
|
|
|
|
График
|
|
|
|
График
|
Замечания.
1) Применяя последовательно эти
приемы, можно построить график функции
вида![]() ;
;
2) Период функций![]() ,
,![]() равен
равен![]() .
.
Примеры.
I. Случай 1), 2).
а)Рассмотрим функцию![]() .
.
График этой функции можно получить
путем сдвига "стандартной" параболы
![]() как единого целого на 2 единицы по оси
как единого целого на 2 единицы по оси![]() вправо и на 1 единицу по оси
вправо и на 1 единицу по оси![]() вверх (см. рис.3).
вверх (см. рис.3).

б)Рассмотрим функцию![]() .
.
График этой функции можно получить
путем сдвига "стандартной" гиперболы
![]() по оси
по оси![]() влево на 1 единицу и по оси
влево на 1 единицу и по оси![]() вверх на 1 единицу (см. рис.4).
вверх на 1 единицу (см. рис.4).

II. Случаи 3), 4).
а)Рассмотрим функцию![]() .
.
График этой функции можно получить
путем растяжения графика
![]() вдоль оси
вдоль оси![]() в 2 раза. При этом нули обеих функций
одинаковы – это точки вида
в 2 раза. При этом нули обеих функций
одинаковы – это точки вида![]() ,
,![]() (см. рис.5).
(см. рис.5).

б)Рассмотрим функцию![]() .
.
График этой функции можно получить из
графика
![]() путем сжатия его в 2 раза к оси
путем сжатия его в 2 раза к оси![]() .
Период функции
.
Период функции![]() равен
равен![]() (см. рис.6).
(см. рис.6).

III. Случаи 5), 6).
Рассмотрим функции
![]() и
и![]() .
.
Их графики можно получить из графика
функции
![]() по правилам 5) или 6) (см. рис.7 и рис.8).
по правилам 5) или 6) (см. рис.7 и рис.8).
Рис. 8
IV. Случаи 7), 8).
Рассмотрим функции
![]() и
и![]() .
.
Их графики можно получить из графика
функции
![]() по правилам 7) и 8), соответственно (см.
рис.9 и рис.10).
по правилам 7) и 8), соответственно (см.
рис.9 и рис.10).

Задачи для самостоятельного решения.
I. Построить графики функций (методом сдвига и растяжения вдоль осей координат):
|
1)
|
9)
|
|
2)
3)
4)
5)
6)
7)
8)
|
10)
11)
12)
13)
14)
15)
|
II.
а)Даны декартовы координаты точки![]() :
:![]() .
.
Найти ее полярные координаты
![]() и
и![]() .
.
б)Даны полярные координаты точки![]() :
:![]() .
.
Найти ее декартовы координаты
![]() и
и![]() .
.
в)Задать кривые в полярных координатах
при помощи уравнения![]() :
:![]() ,
,![]() .
.
Ответы:
II.а)![]() ;б)
;б)![]() ;в)
;в)![]() ,
,![]() .
.
Занятие 3.
Предел функции. Непрерывность функции.
Вычисление пределов непрерывных, рациональных и некоторых иррациональных функций.
Определение 1. Число![]()
![]() называется пределом функции
называется пределом функции![]() при
при![]() ,
стремящемся к
,
стремящемся к![]()
![]() ,
если для любого числа
,
если для любого числа![]() существует число
существует число![]() (зависящее от
(зависящее от![]() ),
такое, что для любого
),
такое, что для любого![]() ,
удовлетворяющего условию
,
удовлетворяющего условию![]() ,
выполнено неравенство
,
выполнено неравенство
![]() .
.
Пишем:![]() .Говорим: Предел
.Говорим: Предел![]() при
при![]() ,
стремящемся к "
,
стремящемся к "![]() ",
равен "
",
равен "![]() "
(или:
"
(или:![]() стремится к "
стремится к "![]() "
при
"
при![]() ,
стремящемся к "
,
стремящемся к "![]() ").
").
Определение 2.Число![]() называется пределом функции
называется пределом функции![]() при
при![]()
![]() ,
если для любого числа
,
если для любого числа![]() существует число
существует число![]() (зависящее от
(зависящее от![]() ),
такое, что для всех
),
такое, что для всех![]() ,
удовлетворяющих условию
,
удовлетворяющих условию
![]() ,
,
выполнено неравенство
![]() .
.
Пишем:
![]() (или
(или![]() ,
,![]() ).
).
Некоторые свойства пределов.
 ;
; ;
; (
( –
константа);
–
константа); ,
, ;
; ;
;
Определение.Функция![]() называетсянепрерывнойв точке
называетсянепрерывнойв точке![]() ,
если: 1)
,
если: 1)![]() определена при
определена при![]() ;
2) существует
;
2) существует![]() ;
3)
;
3)![]() .
.
Теорема.Все элементарные функции непрерывны во всех точках своих областей определения.
Далее мы рассмотрим ряд стандартных пределов (непрерывной, рациональной, иррациональных функций) и сформулируем правила их вычисления.
Вычисление пределов вида
![]() ,
где
,
где![]() –
–
функция, непрерывная в точке а.
Правило:Воспользоваться формулой:
![]() .
.
Примеры:
 ;
; ;
;
Вычисление пределов вида
![]() ,
где
,
где![]() –
–
многочлены (неопределенность вида
![]() ).
).
Правило:

Замечание. Функция
![]() ,
где
,
где
![]() –многочлены, называетсярациональной.
–многочлены, называетсярациональной.
Примеры:
 ;
; ;
; .
.
Вычисление пределов вида
![]() ,
где
,
где![]() –
многочлены, причем
–
многочлены, причем![]()
(неопределенность вида
![]() ).
).
Правило. В этом случае надо сократить
числитель и знаменатель на![]() один или несколько раз.
один или несколько раз.
Пример:
 .
.
Замечания.
Если
 или
или ,
то предел находим непосредственно.
,
то предел находим непосредственно.
Примеры:
 ;
; ;
; .
.
б) Задачи такого типа составляются
и решаются следующим образом. Берем
любые числа![]() :
:
![]() .
.
Вычисление пределов некоторых иррациональных
функций.
Правило 1.Ввести новую переменную
"![]() "
так, чтобы можно было извлечь все корни,
содержащиеся в функции (обычно функция
содержит более одного корня; эти корни
– разной степени).
"
так, чтобы можно было извлечь все корни,
содержащиеся в функции (обычно функция
содержит более одного корня; эти корни
– разной степени).
Пример.
 .
.
Мы сделали замену:
![]() ;
при
;
при![]()
![]() .
.
Правило 2.Перевести иррациональность из числителя в знаменатель или наоборот.
Пример.
![]() .
.
Умножили числитель и знаменатель на
выражение
![]() ,
сопряженное числителю. В результате
преобразований корни из числителя
"исчезли", но появились в знаменателе.
,
сопряженное числителю. В результате
преобразований корни из числителя
"исчезли", но появились в знаменателе.
Замечание.Задачи такого типа
составляются и решаются следующим
образом. Берем любые числа![]() и
и![]() :
:

В случае примера 11:
![]() .
.
Правило 3.Разделить числитель и
знаменатель на "![]() "
в наивысшей степени, встречающейся в
функции (возможно, после некоторых
преобразований функции). Обычно в этих
случаях
"
в наивысшей степени, встречающейся в
функции (возможно, после некоторых
преобразований функции). Обычно в этих
случаях![]() .
.
Пример.
 .
.

