Задачи для самостоятельного решения

; ; ; ; ; ; ; ;

; ; ; ; ; ; .

Ответы:

1)1;2);3)0;4)-2;5);6)4;7);8);9)3;

10) ; 11); 12) 1; 13); 14) 2; 15).

Занятие 4.

Первый и второй замечательные пределы.

Вычисление пределов вида .

Бесконечно малые и бесконечно большие величины.

Определение.Первыйзамечательный предел:.Второйзамечательный предел:.

(Следствия из второго замечательного предела: ;).

Обобщения1-го и 2-го замечательных пределов:

;,

где при.

Нахождение пределов вида .

Правило.

1. Если существует ,;

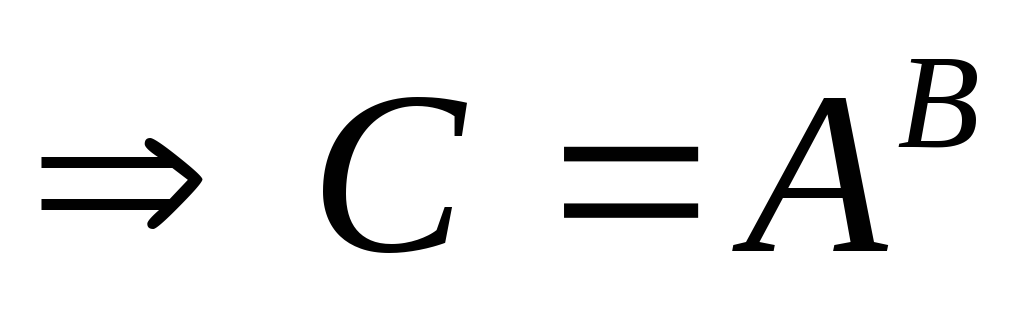2. Если существует ,

находим непосредственно

(, т.е. величиназависит от знака при символе "" и от того,или. Таким образом, либо, либо).

3. Если ,, то полагаем, гдепри, и находимпо формуле:.

Бесконечно малые и бесконечно большие величины.

Определение 1.Если, тоназываетсябесконечно малой (большой)величиной (или функцией) при.

Определение 2.Если(– бесконечно малые), тоиназываютсяэквивалентными бесконечно малыми.Пишем:при.Говорим: "эквивалентнапри".

Теорема.Пусть,при(– бесконечно малые функции). Тогда:

.

Таблица эквивалентных бесконечно малых функций при (при).

1. ;8. ;

2. ;9.

3. ; (– натуральное число).

4. ;

5. ;

6. ;

7. ;

Примеры:

1. ,

;

2. ,

;

3. ;

4. (при);

5. (при);

6. ,

(при);

7. (при);

8. ,

(при);

9. ,

(при);

10. ,

(при; сделали преобразование – разделили числитель и знаменатель на "");

11. ,

(произведение бесконечно малой функции на ограниченную функцию– это бесконечно малая функция, поэтому вышеуказанный предел равен нулю).

Задачи для самостоятельного решения

1); 2); 3); 4); 5);

6) ; 7) ; 8) ; 9) .

Ответы:

1);2);3);4);5);6);7);8);9)2.

Занятие 5. Точки непрерывности и точки разрыва функции. Классификация точек разрыва. Исследование функции на непрерывность.

Определение.Точканазываетсяточкой разрыва функции, если в этой точке функция не является непрерывной.

Замечание. В точке разрываможет нарушаться одно или несколько из условий 1), 2), 3), определяющих непрерывность в точке. Например,илине определено; не существует конечный;.

Определение.Левосторонний (правосторонний) предел функциипри, обозначаемый через(), определяется формулой:

Замечание. Эти пределы иногда называются левым (правым) пределом функциив точкеи вместо записииспользуется запись, т.е.:

.

Теорема. Предел функциив точкесуществует тогда и только тогда, когда существуют и равны между собой левый и правый пределыв точке. В этом случае

.

Классификация точек разрыва

Определение. Точканазываетсяточкой разрыва I-го рода, есликонечный. Если в точке разрываI-го рода, то эта точка называетсяточкой устранимого разрыва, если же– тоточкой неустранимого разрыва. Точканазываетсяточкой разрыва II-го рода, если хотя бы один из односторонних пределовне существует или равен бесконечности.

Геометрическая иллюстрация этих определений:

Примеры:

1. Как выбрать число , чтобыбыла непрерывна в точке?

▲ Функция непрерывна в точке.

Найдем . Поэтому.

2. Как выбрать число , чтобыбыла непрерывна в точке?

▲ Имеем: .

Функция непрерывна в точке.

Отсюда получаем: , т.е..

3. Сформулируем общий принцип построения и решения задач типа 1) и 2). Функция 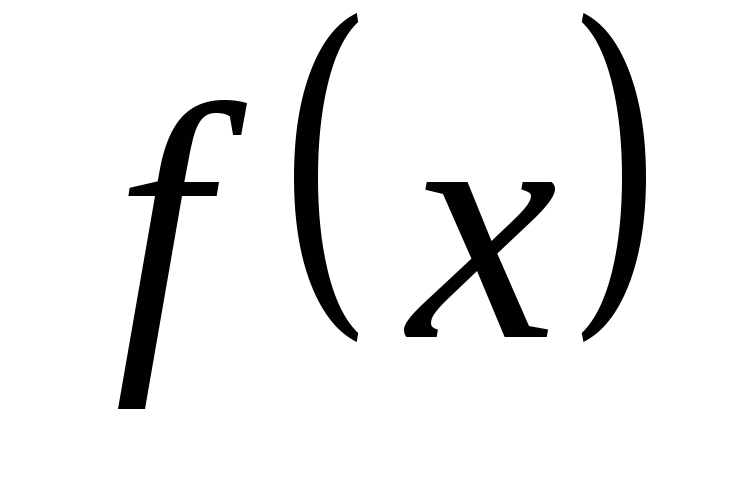задается формулой:

где – некоторые параметры,– фиксированная точка. Требуется подобрать значения параметровтак, чтобыбыла непрерывна в точке.

▲ Находим односторонние пределы функции в точке :

,.

Для непрерывности в точкенеобходимо и достаточно, чтобы, т.е.

(*)

Как правило, функции непрерывны, так что вычисление соответствующих пределов не составляет труда. Из получаемых соотношений (*) находим.

4. Как доопределить функцию в точке, чтобыстала непрерывной в точке?

а) ; б); в)

▲ Для непрерывности в точкенеобходимо и достаточно, чтобы. Поэтому:

а) (произведение бесконечно малой функциина ограниченную функциюесть бесконечно малая функция);

б) ;

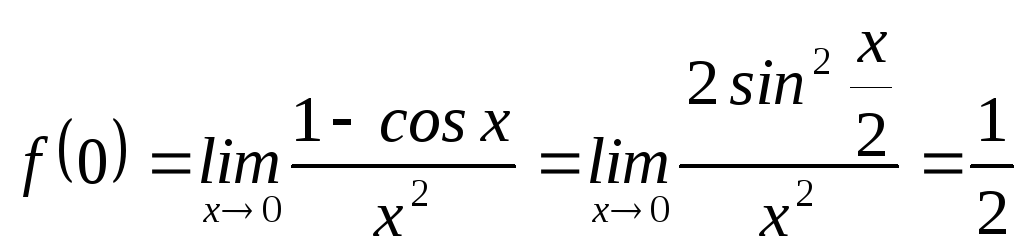в)

.

Замечание. Для построения задач типа 4) можно взять любую функциюиз раздела "Вычисление пределов", для которой пределусоответствует неопределенность вида.

5. Исследовать функцию на непрерывность:

а) .

▲ Точка – точка разрыва, т.к. функция в ней не определена; это – точка разрываI-го рода; устранимого разрыва, т.к.

б).

▲ Функция непрерывна во всех точках, кроме точки . В этой точке – разрыв, т.к.не определена в этой точке. Это точка разрываI-го рода, причем разрыв неустранимый, т.к.

,.

в) .

▲ Функция непрерывна во всех точках, кроме точек вида ,. В этих точках – разрыв, т.к.не определена в них. В точкеразрывI-го рода, причем устранимый, т.к.

.

В точках вида – разрывII-го рода, т.к.

.

г) .

▲ Функция непрерывна во всех точках, кроме точки . В этой точке разрыв, т.к.не определена в этой точке. В точке– разрывI-го рода, причем неустранимый, т.к.

,.

д) .

▲ Функция непрерывна во всех точках, кроме точки . В этой точке – разрыв, т.к.не определена в этой точке. В точке– разрывII-го рода, т.к.

,

.

е) .

▲ Функция непрерывна во всех точках, кроме точки . В этой точке – разрыв, т.к.не определена в этой точке. В этой точке – разрывI-го рода, причем неустранимый, т.к.

,

.