3)Теорема Гаусса.

Рассмотрим точечный положительный электрический заряд q, находящийся внутри произвольной замкнутой поверхностиS(рис. 1.3). Поток вектора индукции через элемент поверхности dSравен(1.4)

Поток вектора электрической индукции через замкнутую поверхность произвольной формы равен алгебраической сумме зарядов, охваченных этой поверхностью:

   (1.5)

Следует отметить, что заряды q_i не обязательно должны быть точечными, необходимое условие - заряженная область должна полностью охватываться поверхностью. Если в пространстве, ограниченном замкнутой поверхностью S, электрический заряд распределен непрерывно, то следует считать, что каждый элементарный объём dV имеет заряд . В этом случае в правой части выражения (1.5) алгебраическое суммирование зарядов заменяется интегрированием по объёму, заключённому внутри замкнутой поверхности S:

(1.6)

Выражение (1.6) является наиболее общей формулировкой теоремы Гаусса: поток вектора электрической индукции через замкнутую поверхность произвольной формы равен суммарному заряду в объеме, охваченном этой поверхностью, и не зависит от зарядов, расположенных вне рассматриваемой поверхности. Теорему Гаусса можно записать и для потока вектора напряженности электрического поля:

_.

Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε₀ и диэлектрическую проницаемость .

ΔΦ = E ΔS cos α = E_n ΔS,

Из теоремы Гаусса следует важное свойство электрического поля: силовые линии начинаются или заканчиваются только на электрических зарядах или уходят в бесконечность.

Дифференциальная форма теоремы Гаусса. Отметим, что интегральная форма теоремы Гаусса характеризует соотношения между источниками электрического поля (зарядами) и характеристиками электрического поля (напряженностью или индукцией) в объеме V произвольной, но достаточной для формирования интегральных соотношений, величины. Производя деление объема V на малые объемы V_i , получим выражение

справедливое как в целом, так и для каждого слагаемого. Преобразуем полученное выражение следующим образом:

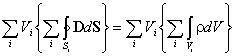(1.7)

и рассмотрим предел, к которому стремится выражение в правой части равенства, заключенное в фигурных скобках, при неограниченном делении объема V. В математике этот предел называют дивергенцией вектора (в данном случае вектора электрической индукции D):

Дивергенция вектора D в декартовых координатах:

Таким образом выражение (1.7) преобразуется к виду:

_.

Учитывая, что при неограниченном делении сумма в левой части последнего выражения переходит в объемный интеграл, получим

Или для вектора напряженности электростатического поля

.

Эти равенства выражают теорему Гаусса в дифференциальной форме.

А)Точечный заряд :

Напряженность поля точечного заряда:

Б)Сфера :

1. Напряженность поля заряженной проводящей сферы радиуса R. Сфера заряжена по поверхности.

А) Внутри сферы заряда нет . Е=0

Б) Снаружи сферы.

На поверхности сферы:

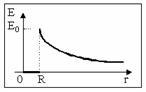
В)Шар :

Введем понятие объемной плотности заряда:

Объемная плотность заряда показывает, какой заряд содержится в единице объема заряженного по всему объему тела.

Объем шара произвольного радиуса

Тогда заряд сферы радиуса r, будет:

Следовательно:

Г)Плоскость :

Введем понятие поверхностной плотности заряда: .

Тогда .

 

Коэффициент 2 появляется, т.к. плоскость окружена двумя поверхностями площадью S.Поле бесконечной заряженной плоскости не зависит от расстояния от плоскости! Можно пользоваться, когда расстояние много меньше размеров плоскости.

Д)Заряженная нить :

Во многих задачах электростатики требуется определить электрическое поле по заданному распределению зарядов. Пусть, например, нужно найти электрическое поле длинной однородно заряженной нити (рис. 1.2.5) на расстоянии R от нее.

Поле в точке наблюдения P может быть представлено в виде суперпозиции кулоновских полей, создаваемых малыми элементами Δx нити, с зарядом τΔx, где τ – заряд нити на единицу длины. Задача сводится к суммированию (интегрированию) элементарных полей Результирующее поле оказывается равным

Связь между потенциалом электрического поля и напряженностьюопределяется соотношениями:

; (36)

, (37)

Потенциал поля точечного заряда в однородной и изотропной среде с диэлектрической проницаемостьюможно определить по формуле

,

Потенциал заряженной нити