Билет № 24.
1). Метод Зейделя, метод верхней релаксации, методы факторизации, доказательство их сходимости для стационарных двухслойных схем.
2). Решение системы дифференциальных уравнений явным методом Эйлера.
|
Метод Зейделя, метод верхней релаксации, методы факторизации, доказательство их сходимости для стационарных двухслойных схем. Метод Зейделя Пусть решается система уравнений Ax =b , все диагональные элементы которой ненулевые. В итерационном методе Зейделя последовательно уточняются компоненты решения, причем k-я компонента находится из k –го уравнения. Именно, если xn = (xn1,......,xnm)T,то следующее приближение определяется из системы соотношений a11 xn+11 + a12 xn2 +.........+ a1mxnm = b1 , a21 xn+11 + a22 xn+12 + a23 xn3.........+ a2mxnm = b2, . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . am1 xn+11 + am2 xn+12+.........+ amm xn+1m = bm. Эту систему можно представить в виде Bxn+1 + Cxn = b, где
a11
0
0 . . . 0
0 a12
a13
. . .
a1m B= a21 a22 0 . . . 0 , C= 0 0 a23 . . . a2m . . . . . . . . . . . . . . am1 am2 am3 . . .amm0 0 0 . . . 0
Отсюдаполучаем xn+1 = -B-1Cxn + B-1b Таким образом, метод Зейделя эквивалентен некоторому методу простой итерации; поэтому для его сходимости при любом начальном приближении необходимо и достаточно, чтобы все собственные значения матрицы B-1C по модулю были меньше 1. Метод верхней релаксации
Модифицируем
метод Зейделя. С этой целью введем
параметр
В данном случае При Соотношению (1) можно придать вид Такая
форма записи показывает, что параметр
Для построения
алгоритма вычисления очередной
итерации нужно разделить в левой части
рекуррентной формулы (2) члены, содержащие
Если
перейти от векторной записи к записи
в виде отдельных уравнений, то можно
получить для компонент
Исследуем условия
сходимости метода верхней релаксации
при дополнительном предположении,
что матрица
Составим для
рассматриваемого случая матрицу
Запишем условие ее положительной определенности Второе слагаемое в выражении (7) не дает вклада в квадратичную форму (8) в силу соотношения(6).
Матрица
Метод
Зейделя, соответствующий случаю
Методы факторизации Факторизованное представление матрицы - представление матрицы в виде произведения матриц, они более простые, чем исходная. B(x1
-x0)/τ
+ Ax0
= Y; (1) B=
τAτA(x1
-x0)
/τ + A x0
=Y;
Ax1
-
Ax0
+
Ax0
=
Y;
Ax1 = Y;
Требования к матрице В:
факторизованное представление:
A=A1 + A2 ; A1 = A2T;
A1
=
A1
+
1/2D;
=0+ + 0
A2=
A2+
1/2D;
AA1 DA2 рассмотрим матрицу В:
B=(E- τ/2 A1 ) (E+ τ/2 A2 ); утверждение: схема (1) сходится из любого начального приближения при такой матрице В,длялюбх значений τ
|
|
Метод Эйлера
Пусть требуется найти приближенное решение дифференциального уравнения y' = f(x,y), удовлетворяющее начальному условию y(x0) = y0. При решении задачи методом Эйлера приближенное значение y1 решения y(x) в точке x вычисляется по формуле y1 = y0 + (x-x0)f(x0,y0). Приближенные значенияyi решения уравнения y(x) в точках xi = x0 +ih, i=1,2,...,n вычисляются по формулам yi+1 = yi + hf(xi,yi). Метод Эйлера является одношаговым методом первого порядка. Локальная погрешность метода Эйлера равна O(h2)
|




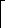
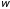 и запишем
и запишем . (1)
. (1) ,
, . (2)
. (2)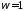 мы возвращаемся к методу Зейделя.
мы возвращаемся к методу Зейделя.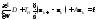 . (3)
. (3)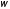 влияет на диагональ матрицы
влияет на диагональ матрицы .
. и
и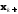 , и придать ей форму:
, и придать ей форму: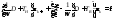 . (4)
. (4)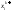 очередной итерации формулы:
очередной итерации формулы: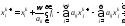 ,
,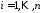 . (5)
. (5) удовлетворяет условиям теоремы
Самарского(А=Ат>0
–самосопряженная положительно
определенная). Самосопряженность
матрицы
удовлетворяет условиям теоремы
Самарского(А=Ат>0
–самосопряженная положительно
определенная). Самосопряженность
матрицы
 означает, что
означает, что ,
,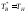 .
Отсюда следует
.
Отсюда следует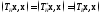 . (6)
. (6) .
Согласно (2)
.
Согласно (2)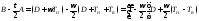 . (7)
. (7)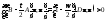 . (8)
. (8) является, по предположению, положительно
определенной. Следовательно, все ее
диагональные элементы строго
положительны:
является, по предположению, положительно
определенной. Следовательно, все ее
диагональные элементы строго
положительны: ,
,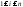 .
Это означает положительную определенность
матрицы
.
Это означает положительную определенность
матрицы :
: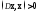 .
В результате знак выражения (8)
определяется знаком первого множителя,
так что достаточное условие для
сходимости итерационной последовательности
метода верхней релаксации принимает
вид:
.
В результате знак выражения (8)
определяется знаком первого множителя,
так что достаточное условие для
сходимости итерационной последовательности
метода верхней релаксации принимает
вид:
 ,
удовлетворяет этому условию.
,
удовлетворяет этому условию.