Math / Матан

↑ назад в содержание ↑

9.Каковы условия параллельности и перпендикулярности прямых?

Условие перпендикулярности прямых:

оказываются перпендикулярными когда

Условие параллельности прямых:

Две прямые будут являться параллельными( или совпадающими) когда их нормали коллинеарны

4. Условия параллельности двух прямых:

а) Если прямые заданы уравнениями с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k1 = k2.

б) Для случая, когда прямые заданы уравнениями в общем виде, необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

5. Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

Это условие может быть записано также в виде

k1k2 = -1.

б) Если уравнения прямых заданы в общем виде, то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства

A1A2 + B1B2 = 0.

↑ назад в содержание ↑

10.Что такое общее уравнение плоскости в пространстве? Что можно узнать о плоскости по ее уравнению?

Уравнение плоскости:

Ax+By+Cz+D= 0

Общее уравнение плоскости :

Ax+By+Cz+D=0

Из уравнения плоскости можно узнать из каких координатах Ox,Oy,Oz, плоскость пересекает оси Ox,Oy,Oz.

↑ назад в содержание ↑

11.Угол между плоскостями. Условия их параллельности и перпендикулярности. Расстояние от точки до плоскости.

Угол между плоскостями равен углу между их нормалями :

В частности 2 плоскости перпендикулярны :

Две плоскости будут параллельны ( или совпадают) когда их нормали коллинеарны Расстояние от точки до плоскости :

↑ назад в содержание ↑

12.Как задается прямая в пространстве? Что такое ее канонические уравнения?

Всякая прямая в пространстве есть линия пересечения двух плоскостей. Прямая в пространстве задается следующей системой уравнений:

!замечание

КАНОНИЧЕСКИЕ уравненияэто уравнения вида:

- координаты точки лежащие на этой прямой

↑ назад в содержание ↑

13.Угол между прямыми, их параллельность и перпендикулярность.

Углом между двумя прямыми называется угол между их направляющими векторами.

−1

=

−1

=

−1

;

−2

=

−2

=

−2

;

1

1

1

2

2

2

Это уравнения двух прямых.

_ _

1= ( 1; 1; 1); 2 = ( 2; 2; 2)

cos =	1, 2		=			1 2+ 1 2+ 1 2
	| 1|×| 2|
			2			2	2	2		2	2
					1	+ 1	+ 1	+ 2		+ 2	+ 2

Условие параллельности прямых

1

2

Введем точку 1 и точку 2, где 1 лежит на первой прямой, а 2 на второй.

Прямые параллельные если 1 2 не коллинеарен направляющим векторам.

Чтобы 2 прямые были перпендикулярными (в пространстве) необходимо, чтобы направляющие этих прямых были перпендикулярны, т.е. косинус угла между ними равен нулю.

cos( 1; 2) = 0.

↑назад в содержание ↑

14.Что такое кривые второго порядка?

Что такое кривые 2-ого порядка?

Кривые 2-ого порядка – это кривые, задаваемые в декартовой системе координат на плоскости уравнениями 2-ой степени т.е. уравнениями вида:

2 + + 2 + + + = 0 , где хоть один из a,b,c ≠ 0.

Перечислим шесть важнейших частных случаев общего уравнения (1):

1) Уравнение эллипса

сполуосями длины и . В частности, при уравнение окружности

сцентром в начале координат и радиусом .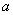

2) Уравнение гиперболы

с полуосями и .

3)Уравнение параболы

4)Уравнение пары пересекающихся прямых:

.

5) Уравнение пары параллельных или совпадающих прямых

.

6) Уравнение, определяющее точку,

.

↑ назад в содержание ↑

15.Напишите канонические уравнения окружности, эллипса, гиперболы и параболы. Как они выглядят?

1) Канонические уравнения эллипса:

2	+	2	= 1
2		2

(При этом фигуру на плоскости называют ограниченной, если она вся помещается в прямоугольник.)

2)Гиперболы:

Гиперболой называют множество всех точек на плоскости, для каждой из которых разность расстояний до 2-х фиксированных точек, называемых фокусами этой гиперболы, есть величина постоянная и притом меньшая, чем расстояние между фокусами.

1. Каноническая гипербола симметрична относительно и , а потому и относительна

начала координат .

2.Гипербола пересекает в точках (-a; 0),(a;0)

3.Гипербола - не ограниченная фигура.

2	−	2	= 1
2		2

3)Параболы:

Параболой называют множество всех точек, для каждой из которых называемой фокусами параболой равно расстоянию до фиксированной G называемой директрисой.

M

F

2 = 2 , где p ≠ 0

4)Окружность:

(x − a)2 + ( − )2 = 2

Окружность - множество всех точек плоскости, равноудаленных от данной точки на плоскости.

Выведем каноническое уравнение:

Пусть C(a, b) – центр окружности, а R – ее радиус. Возьмем произвольную точку M(x, y) окр.

Расстояние от центра окружности до точки M находится по известной формуле

Каноническое уравнение окружности. В центре с координатами a и b и радиусом R Если в этом уравнении раскрыть скобки и выполнить некоторые преобразования,

то получим:

↑ назад в содержание ↑

16.Что такое поверхности 2-го порядка?

Поверхность 2-ого порядка это поверхности 2-ой степени в декартово системе координат:

2 + 2 + 2 + + + + + + + = 0

Причем один из A,B,C,D,E,F≠0.

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат

уравнением a > 0, b > 0, c > 0, называется эллипсоидом.

Рисунок 5.7.1

Свойства эллипсоида.

1.Эллипсоид – ограниченная поверхность, поскольку из его уравнения следует,

что

2.Эллипсоид обладает

центральной симметрией относительно начала координат,

осевой симметрией относительно координатных осей,

плоскостной симметрией относительно начала координат.

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат

уравнением a > 0, b > 0, называется эллиптическим параболоидом.

Свойства эллиптического параболоида.

1.Эллиптический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z ≥ 0 и принимает сколь угодно большие значения.

2.Эллиптический параболоид обладает

осевой симметрией относительно оси Oz,

плоскостной симметрией относительно координатных осей Oxz и Oyz.

3.В сечении эллиптического параболоида плоскостью, ортогональной оси Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy – парабола.

Определение 5.14.

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат

уравнением a > 0, b > 0, называется гиперболическим параболоидом.

Рисунок 5.7.3

Свойства гиперболического параболоида.

1.Гиперболический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.

2.Гиперболический параболоид обладает

осевой симметрией относительно оси Oz,

плоскостной симметрией относительно координатных плоскостей Oxz и Oyz.

3.В сечении гиперболического параболоида плоскостью, ортогональной оси координат Oz, получается гипербола, а плоскостями, ортогональными осям Ox иOy, – парабола.

4.Гиперболический параболоид может быть получен поступательным перемещением в пространстве параболы так, что ее вершина перемещается вдоль другой параболы, ось которой параллельна оси первой параболы, а ветви направлены противоположно, причем их плоскости взаимно перпендикулярны.

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат

уравнением

a > 0, b > 0, c > 0, называется двуполостным гиперболоидом.

Рисунок 5.7.5

Свойства двуполостного гиперболоида.

1.Двуполостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует,

что и неограничен сверху.

2.Двуполостный гиперболоид обладает

центральной симметрией относительно начала координат,

осевой симметрией относительно всех координатных осей,

плоскостной симметрией относительно всех координатных плоскостей.

3.В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz,

при получается эллипс, при – точка, а в сечении плоскостями, перпендикулярными осям Ox и Oy, – гипербола.

По аналогии с коническими сечениями существуют и вырожденные поверхности второго порядка. Так, уравнением второго порядка x2 = 0 описывается пара совпадающих плоскостей, уравнением x2 = 1 – пара параллельных плоскостей, уравнением x2 – y2 = 0 – пара пересекающихся плоскостей. Уравнениеx2 + y2 + z2 = 0 описывает точку с координатами (0; 0; 0), уравнение x2 + y2 = 1 – круговой цилиндр, уравнение x2 + y2 = z2 – круговой конус. Существуют и другие вырожденные случаи. Полная теория поверхностей второго порядка рассматривается в курсе аналитической геометрии.

↑ назад в содержание ↑

17.Напишитеуравнения сферы и обоих параболоидов. Как они выглядят?

1) − 2 + − 2 + − 2 = 2 сфера.

Y

X

Z

2) = 2 + 2 Эллиптический параболоид

1) Гиперболический параболоид.

Z= 2 − 2

↑ назад в содержание ↑