Math / Матан

	1) =		1	,	= 0
	2) = tan ,					=		+
							2

Разумно ввести классификацию точек разрыва, по возрастанию сложности.

1) «а» - устранима, если lim ≠

→

Примеры:

1.	sin		, = 0		f(a) не определена
				sin	при ≠ 0
2.			=			a=0
				5 при = 0

2) Говорят что a – точка разрыва типа скачка, если конечные

lim→ −0 =	lim ( )
	→+0

Иногда устранимые точки вместе со скачками называют точками разрыва 1-го рода.

Все остальные точки разрыва называют разрывами 2-го рода.

↑ назад в содержание ↑

(28)77.Что такое линейная система уравнений? Какие системы называют равносильными? Примеры.

В линейной алгебре изучают системы линейных уравнений , методы их решения и связанные с этим вопросы.

Линейными называют уравнения вида:

a1x1+ a2x2 + … + anxn = b

Числаa1, … , anназывают коэффициентом такого уравнения, а b–

его свободным членом. Мы будем рассматривать системы из

нескольких линейных уравнений, при чем число неизвестных в такой системе может не совпадать с числом уравнений.

Существуют различные методы решения линейных систем. Наиболее универсальным среди них является т. н. метод Гаусса (последовательного исключения неизвестных). Этот метод основан на преобразовании данной системы к удобному виду. Изложим связанные с этим понятия: Система называется совместной, если она имеет хотя бы одно решение. Если у системы нет решений, она называется несовместной.

Две системы уравнений, обладающие одним и тем же множеством решений, называются равносильными (эквивалентными). Примеры:

↑ назад в содержание ↑

(29)78.Что такое элементарные преобразования?

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность(равносильность) матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.

Элементарными преобразованиями строк называют:

перестановка местами любых двух строк матрицы;

умножение любой строки матрицы на константу , ;

прибавление к любой строке матрицы другой строки.

↑назад в содержание ↑

(30)79.Что такое ступенчатая система? Примеры.

Под ступенчатой системой линейных уравнений понимается система линейных уравнений со ступенчатой матрицей коэффициентов, т. е.:

1.все нулевые строки находятся в матрице ниже ненулевых строк;

2.если (0,...,0,aik,...,ain), - первый ненулевой элемент в i -й строке (называемый лидером i - й строки), то ars=0 для всех , 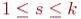(элементы ars=0 для всех мест (r,s), расположенных в строчках, ниже i -й, и в столбцах s=1,2,...,k ). Другими словами, лидер строки с большим номером стоит строго правее.

Ненулевая матрица имеет главный ступенчатый вид, если матрица A имеет ступенчатый вид, все лидеры ненулевых строк ( ) равны 1 и

для каждого j, , в lj -м столбце матрицы A единственный ненулевой элемент - это .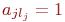

Примеры:

Матрица имеет ступенчатый вид (выделены лидеры строк), но не главный ступенчатый вид.

Матрица имеет главный ступенчатый вид. Нулевая матрица имеет ступенчатый вид.

Матрица не является ступенчатой (нулевая строка находится выше ненулевых строк).

Матрицы не являются ступенчатыми (лидер третьей строки находится не строго правее, чем лидер второй строки).

↑ назад в содержание ↑

(31)80.Как произвольная линейная система приводится к ступенчатому виду? Рассмотрите пример.

Как произвольная линейная система приводится к ступенчатому виду? Рассмотрите пример.

1 + 2 + 3 + 4 + 5 = 5

1 + 2 + 3 3 + 3 4 + 3 5 = 11 из второго и третьего мы вычитаем первое с коэф. 1.

1 + 2 + 3 3 + 3 4 + 4 5 = 12

Пусть нам дана произвольная система в первое уравнение которой входит 1. Вычитая из последующих первое уравнение с подходящим коэффициентом, уничтожим 1 во всех уравнениях системы, кроме первого. Уравнения преобразованной системы, начиная со второго образуют подсистему возникшей системы число неизвестных, в которой и число неизвестных и число уравнений меньше, чем в исходной системе. Дальше по той же схеме преобразуются уравнения этой уменьшенной подсистемы. После некоторого количества таких этапов приходим к ступенчатой системе. Преобразования второго типа используются например тогда, когда в первое уравнение не входит первое неизвестное.

1 + 2 + 3 + 4 + 5 = 5

2 + 3 3 + 3 4 + 3 5 = 11 из третьего мы вычитаем второе с коэффициентом 1.

2 + 3 3 + 3 4 + 4 5 = 12

1 + 2 + 3 + 4 + 5 = 52 + 3 3 + 3 4 + 3 5 = 11

4 5 = 12

↑ назад в содержание ↑

(32)81.Как по Гауссу решается ступенчатая линейная система? Пример.

Покажем, как решать ступенчатые системы

Вначале рассмотрим 2 примера: (двойные скобки нигде ставить не нужно)

				1)
1 + 2 + 3 + 4 = 10			X1 = 10 – 1 – 3 – 4 = 2
2 − 3 + 4	= 2		X2	= 2 + 3 – 4 = 1	Решаем эту систему
3 + 2 4	= 11		X3	= 11 – 8 = 3	снизу вверх
4	= 4		X4	= 4

2)

1 + 2 + 3 + 4 + 5 + 6 + 7 = 0

3 −	5 + 6	= 0
	6	+ 7 = 2

x1 = - t4 – (- t2 -2 - t1) - t3 - t2 – (2 - t1) - t1 ; x2 = t4 ;

x3 = - t2 - 2 - t1 ;
x4	= t3 ;	решаем эту систему снизу вверх
x5	= t2 ;
x6	= 2 - t1 ;
x7	= t1 ;

Как и в рассмотренных примерах, ступенчатые системы решаются «снизу вверх», при этом неизвестные, которыми «открываются» уравнения, называются главными, а все остальные, свободными. Переход к очередному уравнению системы происходит подставлением всех значений известных до этого, присвоении неопределённым до этого свободным от этого независимых параметрических значений и вычисление значения главного переменного этого уравнения.

Процедура Гаусса решения ступенчатых систем показывает, что общее решение ступенчатой системы с r уравнениями и n переменных зависит от n – r, это число

свободных неизвестных параметров

↑ назад в содержание ↑

(33)82.Как устроено множество решений линейной системы уравнений? Примеры.

Система m линейных алгебраических уравнений с n неизвестными (или, линейная система)

в линейной алгебре — это система уравнений вида

Система линейных уравнений от трёх переменных определяет наборплоскостей. Точка пересечения является решением.

Здесь — количество уравнений, а 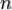— количество неизвестных. x1, x2, …, xn — неизвестные, которые

надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены —

предполагаются известными[1]. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[2].

Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0),

иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

↑ назад в содержание ↑

(34)83.Что такое главные и свободные неизвестные системы? Примеры.

Что такое главные и свободные неизвестные системы?

Начнем с того, что же называется ступенчатой системой, потому что именно там используется главные и свободные неизвестные системы. (это так, на случай если вдруг спросит)

Ступенчатой системой называют систему, в которой 1-ый отличный от нуля коэффициент каждого следующего уровня расположен правее коэффициента предыдущего уровня.

Главными неизвестными системы называют такие неизвестные, которые в строчке системы стоят левее всех и их нельзя заменить какими бы то ни было параметрами.

Свободными неизвестными системы называют неизвестные, которые стоят(или могут стоять) после главных неизвестных и могут быть заменены параметрами.

Примеры:

			Главные неизвестные – X1 (в 1-ой строчке), Х2 (во
X1	+X2 + X3 + X4 = 4
X2	+ + X4 = 2		2-ой строчке), Х4 (в 3-ей строчке)
	X4 = 1		Свободные неизвестные – X2, X3, X4 (в 1-ой
			строчке), X4 (во 2-ой строчке), и нет свободных
			неизвестных в 3-ей строчке (т.к. там имеется только
			один неизвестный, который является главным)

Свободные члены мы можем заменить параметрами. Во всех примерах лучше начинать решать систему снизу вверх. Итак, в 3-ей строчке нет свободных членов, а значит нет и параметров. Во 2-ой строчке тоже нет свободных членов, т.к из 3-ей строки мы подставляем значение Х4 во 2-ую строку, и поэтому здесь тоже нет параметров. А вот в 1-ой строчке свободный член есть, это Х3. Поэтому Х3 следует

заменить параметром t (условное обозначение для параметров; если их несколько, то обозначаются они t1, t2, t3, ect).

↑ назад в содержание ↑

(35)84.Что такое прямоугольные и квадратные матрицы? Примеры.

Матрицей называется прямоугольная таблица чисел, состоящая из m одинаковой длины строк или n одинаковой длины столбцов.

aij- элемент матрицы, который находится в i-ой строке и j-м столбце.

Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.

В общем виде матрицу размером m×n записывают так

.

Примеры:

Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.

Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья.

Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.

Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.

.

Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали,

равны нулю, называется диагональной матрицей. Например,

или

.

Диагональная матрица, у которой все диагональные элементы равны единице,

называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка

имеет вид

.

↑ назад в содержание ↑

(36)85.Что такое линейные операции над матрицами? Примеры.

Во всех случаях, когда вводятся новые математические объекты, необходимо договариваться о правилах действийнад ними, а также определить - какие объекты считаются равнымимежду собой.

Природа объектов не имеет никакого значения. Это могут быть вещественные или комплексные числа, векторы, матрицы, строки или что-то иное.

К числу стандартных действий относятся линейные операции, а именно: умножение на число и сложение; в данном конкретном случае - умножкние матрицы на число и сложение матриц.

При умножении матрицы на число каждый матричный элемент умножается на это число, а сложение матриц подразумевает попарное сложение элементов, расположенных в эквивалентных позициях.

Терминологическое выражение " линейная комбинация<" (векторов, матриц, строк, столбцов и так далее) всегда означает одно и тоже: алгебраическая сумма этих векторов (или матриц, строк, столбцов и так далее), предварительно умноженных на числовые коэффициенты.

Матрицы A = || ai j || и B = || ai j || считаются равными, если они имеют одинаковые размеры и их соответствующие матричные элементы попарно равны:

(1)

для любых допустимых значений индексов i и j.

К линейным операциям над элементами множества или пространства относятся операции сложения элементов и их умножения на скаляр (число).

Умножение матрицы на число

При умножении матрицы A на число λ (слева или справа) каждый ее матричный элемент умножается на это число:

(2)

Сложение матриц

Операция сложения определена только для матриц одинаковых размеров. Результатом сложения матриц A = || ai j || и B = || bi j || является матрица C = || ci j || , элементы которой равны сумме соответствующих матричных элементов:

(3)

Линейной комбинацией матриц A и B называется выражение вида , где и – числовые коэффициенты.

↑ назад в содержание ↑

(37)86.Что такое произведение двух матриц? При каких условиях оно определено? Примеры.

Умноже́ниема́триц — одна из основных операций над матрицами. Матрица, получаемая в результате операции умножения, называется произведе́ниемма́триц.

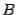Произведением матрицы размеров на матрицу размеров 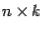называется

матрица размеров , элементы которой вычисляются по формуле

(14.5)

где , .

Операция умножения двух матриц выполнима только в том случае, если число столбцов в первом сомножителе равно числу строк во втором; в этом случае говорят, что форма матрицсогласована. В частности, умножение всегда выполнимо, если оба сомножителя — квадратные матрицы одного и того же порядка.

Найти произведения матриц AB и BA, если

и

Р е ш е н и е: Имеем

↑ назад в содержание ↑

(38)87.Какие операции называют коммутативными? Покажите на примерах, что умножение матриц не коммутативно.

Коммутативность = Перестановочность.

Обычные числа переставлять можно: 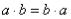, а матрицы в общем случае не перестановочны: .

Какие матрицы можно умножать?

Чтобы матрицу можно было умножить на матрицу нужно, чтобы число столбцов матрицы равнялось числу строк матрицы .

Пример:

Можно ли умножить матрицу на матрицу ?

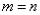, значит, умножать данные матрицы можно.

А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!

, следовательно, выполнить умножение невозможно:

Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.

Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.

Например, для матриц, и возможно как умножение , так и умножение

↑ назад в содержание ↑

(39)88.Что такое единичная и обратная матрицы? Как строится (по Гауссу) обратная матрица?

Пусть a – квадратная матрица порядка n. Обратной к ней матрице называется такая матрица A-1, что A-1*A=E (здесь A-1 и E – квадратные матрицы того же порядка, причём E – единичная матрица).

Это определение вовсе не подразумевает, что обратная матрица существует для любой матрицы A.

Примеры

1.	1		2	1	5		2
		3	5			3	1
	1		2 1 5				2		1	0
		3	5		3		1		0	1
2.	0		0	1	не существует
		0	0

0 0 1

3.не существует

a b

(0 0) – эта строка приводит к тому, что первая строка произведения этой матрицы на любую другую состоит из одних нулей (в единичной матрице это не так)

Определения с википедии:

1.Обратная матрица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

2.Единичная матрица — квадратная матрица, элементы главной диагонали которой равны единице поля, а остальные равны нулю.

Нахождение обратной матрицы методом Гаусса.

Исходная матрица А.

1	2
A =
3	4

Найдем матрицу А-1 обратную к матрице А.

Для этого напишем расширенную матрицу , в левой части которой находится наша исходная матрица А, а в пр единичная.

Применяя метод Гаусса, последовательно будем приводить нашу исходную матрицу (левую часть расшире