Тема: функция двух переменных.

Функция двух переменных

При изучении многих зависимостей используют понятие функции нескольких переменных.

Например: температура Т, измеряемая в различных точках некоторого тела или пространства, зависит от координат точки (х, у, z) (от места, где устанавливается термометр) и от момента времени t. В этом случае пишут T=f(x, у, z, t).

Мы будем рассматривать только случай функций двух переменных. Выводы, полученные при этом, можно легко распространить на функции от большего числа переменных.

Примером функции двух переменных может служить зависимость площади прямоугольника от длины a и от ширины b. формула имеет вид S=a*b Опр. Функция двух переменных – это правило, по которому каждой паре х и у ставится в соответствие единственное значение Z.

Обозначают z=f(x,y), f-закон соответствие по которому паре х и у ставится в соответствие значение Z.

Значение функции двух переменных находится так же как и для функции одной переменной

Например: Вычислить значение функции двух переменных Z=x²–2xy, в точке М(1,2)

Z(1,2)= f(x,y)=1²–2*1*2=1–4= –3

Опр. Область определения функции двух переменных z=f(x,y) называется множество пар переменных х и у для которых функция z=f(x,y) определена.

Область определения может иметь вид прямоугольника, круга, полуплоскости.

П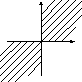ример 1:

Найти область определения для функции Z=

Корень существует, если ху0, это возможно когда

или

о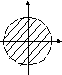бласть определения функции двух переменных обычно изображается штриховкой в системе ПДСК координат на плоскости.

Пример 2:

Найти область определения для функции Z=,

Выражение будет существовать когда корень 0, знаменатель 0

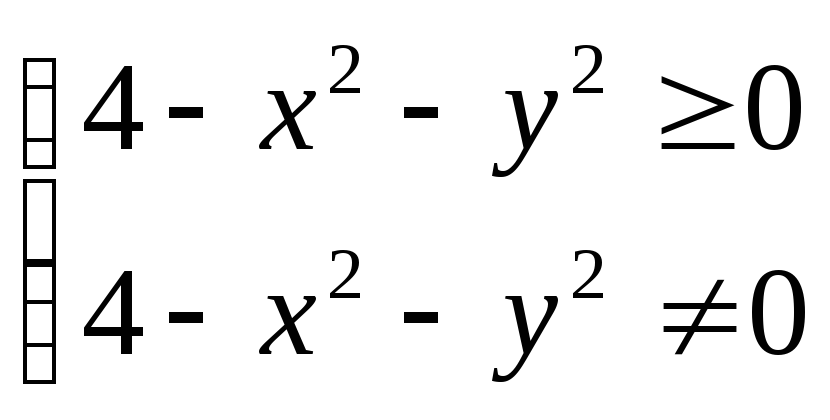, т.е. 4–х²–у²>0

4–х²–у²=0

х²+у²=4 окружность с центром в точке (0,0) и радиусом 2.

Возьмем точку из окружности (0,0) и подставим ее в неравенство, получим верное равенство, следовательно областью определений будет все множество точек лежащее внутри окружности.

Геометрический смысл функции двух переменных.

Дана функция двух переменных z=f(x,y). Каждой точке из области определения с координатами (х,у) соответствует одно значение переменной z=f(x,y). Таким образом определяется упорядоченная тройка чисел (х,у,f(x,y)), таких точек можно получить сколь угодно много, если переменные пробегают всевозможные значения из области определения, то в пространстве получится поверхность – график функции двух переменных.

Например: поверхность определяемая уравнением Z=x²+y² называется параболоид вращения.

Предел функции двух переменных.

Опр. Пределом функции двух переменных называется число к которому стремится сама функция при стремлении аргументов каждый к своему значению. z=f(x,y) , М(х₀,у₀) обозначается

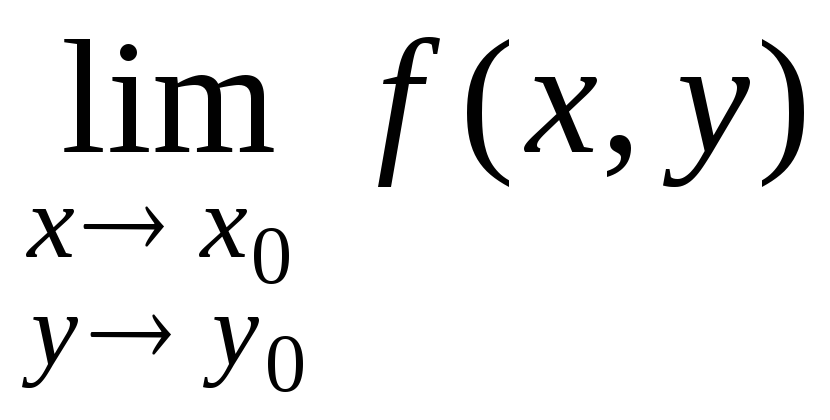
Например: z= x³–4xy² M(-1,0)

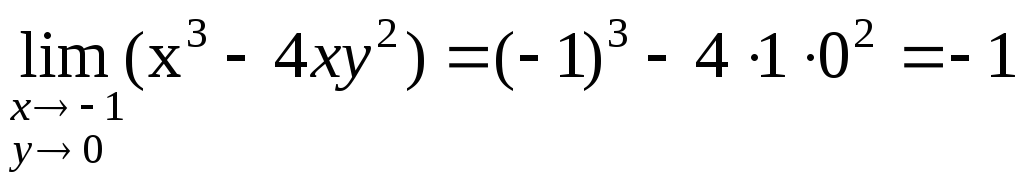
Непрерывность функции двух переменных.

Опр Функция f(х,у) называется непрерывной в точке (х₀;у₀), если бесконечно малым изменениям значений аргументов х и у соответствует бесконечно малое изменение функции f(х,у).

График непрерывной функции представляет собой поверхность без разрывов, «проколов» и других особенностей.

Опр Функция двух переменных называется непрерывной в своей области определения, если она непрерывна в каждой точке этой области.

Частные производные первого и второго порядка.

Рассмотрим функцию Z=f(x,y), зафиксируем переменную у=у₀, тогда из функции двух переменных получим функцию одной независимой переменной Z=f(x,y₀).

Опр. Разность между конечным и начальным значениями функции называется частным приращением функции от данной переменной.

Для х задаем приращение х

f(x+х,y₀)– f(x,y₀)= _хZ– частное приращение по переменной х

Опр. Частной производной функции двух переменных Z=f(x,y) по переменной х называется предел отношения приращения функции по переменной х к приращению аргумента х, при условии что х0.

Обозначают ,Z’_x, f’_x(x,y),

Z’_x=

Аналогично определяем другую частную производную Z’_у

Аналогично фиксируем переменную х=х₀, у-переменная

f(x₀,y+у)– f(x₀,y)= _уZ – частное приращение по переменной у,

Опр. Частной производной функции двух переменных Z=f(x,y) по переменной у называется предел отношения приращения функции по переменной у к приращению аргумента у, при условии что у0.

Z’_у=

Производные от функции двух переменных находится по тем же самым правилам и формулам, как и производная функции одной переменной. Только необходимо помнить, какая из данных переменных зафиксирована, а какая продолжает изменяться.

Пример:

Z= x²–3y²–6xy–2x–y+9 Z’_x =? Z’_у–?

Z’_x = (x²)’_x –(3y²)’_x–(6xy)’_x–(2x)’_x–(y)’_x+(9)’_x =2x–0–6у–2–0+0=2x–6у–2

У=const

Z’_у= (x²)’_у –(3y²)’_у–(6xy)’_у–(2x)’_у–(y)’_у+(9)’_у=0–6у–6х–0–1+0= –6у–6х–1

Частные производные по переменным Х и У, станут новыми функциями двух переменных и при необходимости от них можно найти частные производные как по переменной Х так и по У­– они называются частными производными второго порядка.

Z”_xх – частная производная второго порядка дважды дифференцирован по переменной Х

Z”_уу ,– част пр-я 2-го порядка дважды дифференцирован по переменной У

Z”_ху ,– част пр-я 2-го порядка сначала найденная по перем Х, потом по У

Z”_ух ,– част пр-я 2-го порядка сначала найденная по перем У, потом по Х

Пример: Найти частные производные второго порядка от функции

Z=x²–3y²–6xy–2x–y+9

Z’_x = 2x–6у–2

Z’_у= –6у–6х–1

Z”_xх = (Z’_x)’_х = (2x–6у–2)’_x=2-0-0=2

Z”_yy = (Z’_y)’_y = (–6у–6х–1)’_y=-6-0-0= –6

Z”_xy = (Z’_x)’_y= (2x–6у–2)’_y=0-5-0= –6

Z”_yx = (Z’_y)’_x= (–6у–6х–1)’_x=-0–5–0= –6

Заметим что частные производные второго порядка Z’_xy Z’_yx равны между собой, и следовательно не зависят от порядка дифференцирования.

Экстремум функции двух переменных.

Опр. Функция Z=f(x,y), в точке (х₀;у₀) будет иметь минимум, если для всех других точек с координатами (х;у) будет выполнено следующее условие: f(х₀;у₀)<f(x,y)

Опр. Функция Z=f(x,y), в точке (х₀;у₀) будет иметь максимум, если для всех других точек с координатами (х;у) будет выполнено следующее условие: f(х₀;у₀)>f(x,y)

Максимум и минимум функции как и в случае функции одной переменной будем называть экстремумами функции.

Теорема1: (необходимое условие существования экстремума)

Если функция Z=f(x,y) имеет экстремум в точке (х₀;у₀), то ее частные производные, первого порядка, в этой точке равны нулю.

Т.е. если для Z=f(x,y) (х₀;у₀)–экстремум 

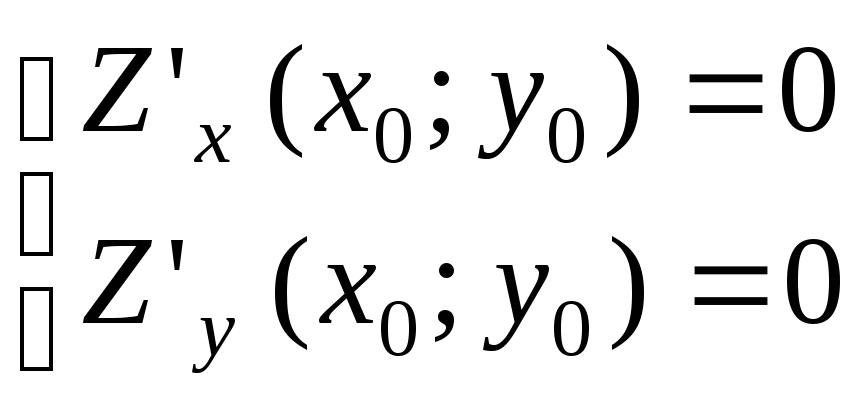
Точки в которых производная равна нулю называют критическими точками.

Теорема2: (достаточное условие существования экстремума)

Пусть функция Z=f(x,y)-непрерывная в области определения вместе со своими производными и точка М₀(х₀;у₀)–критическая точка, обозначим

А=B=C=

если АС–В²>0, то функция имеет экстремум в точке М₀, причем

1. минимум, если А>0

2. максимум, если А<0

3. если АС–В²<0, то точка Мо(х₀;у₀)– не является точкой экстремума

4. если АС–В² =0, то нужны дополнительные исследования на определение точек экстремума (сомнительный случай)

Алгоритм исследования функции двух переменных на экстремум.

1. Найти частные производные первого порядка.

2. Найти критические точки, т.е. решить систему

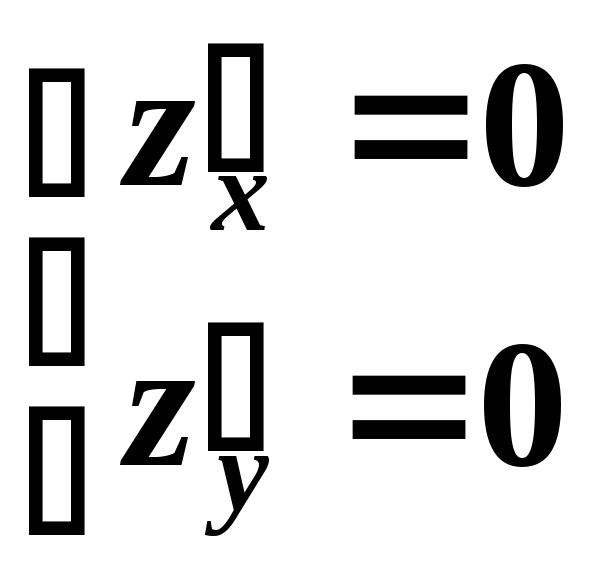
3. Найти частные производные второго порядка, т.е. найти А,В,С.

4. Сделать выводы на основании Т2 о точках экстремума.

Пример: Исследовать на экстремум функцию Z=3x²+3xy+у²–6х–2y+7

1. Z’_x = 6x+3у–6 Z’_у= 2у+3х–2

2. Решим систему:

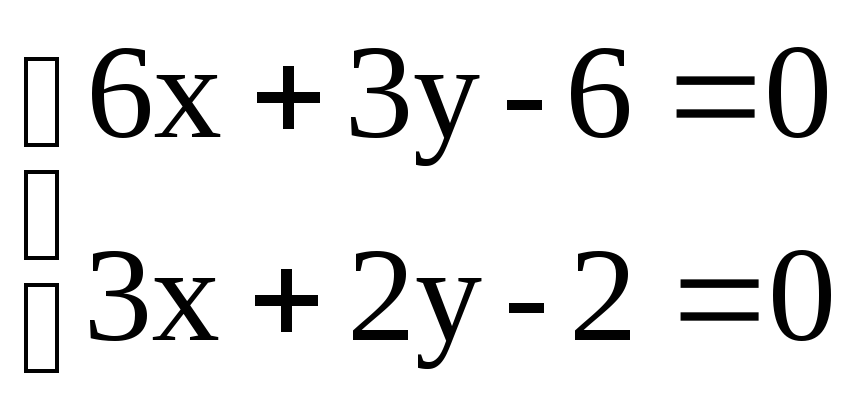у=2–2х

3х+2(2–2х)–2=0 х=2

у=2-2(2)=–2 (2;–2)– критическая точка

3. Z”_xx=6=A Z”_xy=3=B Z”_yy=2=C

4. АС–В²=3 >0 – экстремум есть и т.к. А=6>0 следовательно (2;–2) – точка минимума.

5.

(2;–2;3) – точка минимума.

Касательная плоскость и нормаль к поверхности

Пусть фиксированная точка на поверхности, заданной функцией

Касательной плоскостью к поверхности в точке называется плоскостьt проходящая через эту точку и такая, что угол между этой плоскостью и секущей проходящей через эту точку и любую точку поверхности стремится к нулю.

Уравнение t:

Нормалью называется прямая n, проходящая через точку и перпендикулярно касательной плоскости.

Уравнение n: