lek3

Значит, в правую часть уравнения нужно добавить еще один член. Как же он должен выглядеть? Если электрический заряд с течением времени вытекает из объема через замкнутую поверхность, заключающую в себе этот объем, то напряженность электрического поля уменьшается, и производная от напряженности электрического поля по времени будет отрицательной. Добавив в правую часть уравнения член, содержащий эту производную, можно будет устранить возникшее недоразумение:

	∫	r r		∫	∂E	r
		j dS + ε				dS = 0 ,
			0		∂t
	S			S

что вполне допустимо.

Теперь этот второй член нужно добавить в теорему о циркуляции вектора В. Получим новое уравнение, уравнение Максвелла:

∫	r r		∫	r r		∫	∂E	r	.
	B dl = µ			j dS + µ ε				dS
							∂t
		0		0	0
l			S			S

Это уравнение имеет важный физический смысл. У магнитного поля есть два источника: первый – это движущийся электрический заряд или ток, а второй

– это переменное электрическое поле.

Переменное электрическое поле порождает в пространстве маг-

нитное поле. Это явление и называется явлением магнитоэлектрической индукции.

Выражение

		∂E	r
	ε 0		= jсм
		∂t

получило название вектора поверхностной плотности тока смещения в вакууме или просто ток смещения в вакууме.

СИСТЕМА УРАВНЕНИЙ МАКСВЕЛЛА Четыре уравнения: теорема Гаусса для электрического поля, закон Фа-

радея, теорема Гаусса для магнитного поля и уравнение Максвелла, – составляют систему уравнений Максвелла. Именно Максвелл записал все эти уравнения в той форме, в какой они записаны ниже.

r

r

1

∫E dS =

∫ ρ dV

,

ε

0

S

V

r

r

∂B

r

∫E dl = −∫

dS

,

∂t

l

S

r

∫B dS = 0

,

S

∫

r r

∫

r

r

∫

∂E

r

.

B dl = µ

j dS + µ ε

dS

∂t

0

0

0

l

S

S

Первые два уравнения показывают, как возникает электрическое поле. Во-первых, согласно теореме Гаусса для электрического поля оно создается положительными и отрицательными электрическими зарядами. Это поле имеет потенциальный характер. Во-вторых, согласно закону Фарадея вихревое электрическое поле порождается переменным магнитным полем. Естественно, что это поле имеет вихревой характер.

Вторые два уравнения рассказывают о магнитном поле. Магнитное поле всегда вихревое и имеет только вихревой характер. Поэтому поток вектора магнитной индукции согласно теореме Гаусса для магнитного поля всегда равен нулю. Две причины возникновения магнитного поля: движущийся электрический заряд и переменное электрическое поле, – содержатся в четвертом уравнении.

Обратим еще раз внимание на то, что отличие от нуля потока векто-

ра через любую замкнутую поверхность говорит о потенциальном ха-

рактере поля этого вектора, а отличие от нуля циркуляции вектора по

любому замкнутому контуру говорит о вихревом характере этого поля.

В случае статики, то есть когда электрическое и магнитное поля неизменны (производные по времени равны нулю), система из четырех уравнений разбивается на две системы:

	r r	1				r
	∫E dS =			∫ ρ dV	и	∫E dl = 0	, –	два уравнения электростатики. Электроста-
		ε	0
	S			V		l

тическое поле – поле с потоком, но без циркуляции, имеющее только потенциальный характер.

Потенциальная энергия имеет вид параболы

r	и	r	r	, – два уравнения магнитостатики. Магнитное по-
∫B dS = 0		∫B dl = µ 0	∫ j dS
S		l	S

ле – поле с циркуляцией, но без потока, имеющее только вихревой характер.

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ Свободные колебания осуществляются в так называемых колебатель-

ных системах. Колебательная система – это система тел, в которой имеется «потенциальная яма», то есть потенциальная энергия имеет минимум, соответствующий положению устойчивого равновесия. В колебательной системе при ее смещении из положения равновесия действует консервативная сила, возвращающая систему в положение равновесия. Смещение из положения равновесия обозначим буквой ψ. В механических колебательных системах это координата или угол. В электрических колебательных системах это заряд, сила тока или напряжение.

Ep

						βψ 2
			E	p	=			.
							2
		При этом консервативная возвра-
		щающая сила будет равна
0	ψ		F = −		dE p		= −βψ .
			ψ		dψ
Fψ		Эта сила называется квазиупругой,
		так как по форме похожа на силу
		упругости, возникающую при аб-
0	ψ	солютно	упругих				деформациях.

Квазиупругая сила прямо пропорциональна смещению.

ψ = f (t )

ϕ = ω t + ϕ 0

Используем второй закон Ньютона. Ускорение равно второй производной от смещения по времени. Если в колебательной системе нет трения или сопротивления, уравнение закона будет выглядеть следующим образом:

m		d 2ψ		= −βψ .
		dt 2
Преобразуем это уравнение и представим его в виде
	d 2ψ		+ ω 2 = 0		,
	dt 2
где ω – циклическая частота колебаний, величина которой ω =							β		и измеря-
							m

ется в 1с . Выражение для циклической частоты зависит от вида колебатель-

ной системы.

Это уравнение называется дифференциальным уравнением гармонических колебаний. В случае электрических колебаний роль второго закона Ньютона играет закон Ома, преобразование которого приводит к тому же дифференциальному уравнению гармонических колебаний, но циклическая частота имеет другое выражение.

Решением этого дифференциального уравнения являются гармонические колебания:

ψ = A cos(ω t + ϕ 0 ) .

Гармоническими называются колебания, происходящие по закону косинуса или синуса. Напомним, что sinx и cosx имеют одинаковые графики, лишь cдвинутые вдоль оси 0х (сдвинутые по фазе). В этой формуле А – амплитуда колебаний, – фаза колебаний, а φ0 – начальная фаза. Фаза колеба-

ний – безразмерная величина. На рисунке ниже показан график гармонических колебаний, т.е. график функции ψ = f (t ) .

Гармонические колебания – периодический процесс. Время Т одного полного колебания называется периодом. Через каждый период во времени колебательная система приходит в то же состояние, и функция принимает то же самое значение (см. рисунок).

ψ

А

0

t

T

Поскольку cosϕ = cos(ϕ + 2π ), через каждый период во времени фаза ко-

лебаний изменяется на 2π. Используем это обстоятельство для получения формулы связи периода с циклической частотой. Прибавим период Т к моменту времени t. Получим

ψ (t + T ) = A cos(ω (t + T )+ ϕ 0 ) = A cos(ω t + ϕ 0 + ω T ) = A cos(ω t + ϕ 0 + 2π ),

откуда следует, что ωT = 2π . Итак,

T = 2π .

ω

Период колебаний обратен частоте: Т = 1 , а циклическая частота связа-

ν

на с частотой равенством ω = 2π ν . В отличие от циклической просто частота измеряется в Гц (Герцах). 1 Гц = 1/с.

ВОЛНА. УРАВНЕНИЕ ВОЛНЫ Колебания, происходящие в одной точке пространства, возбуждают ко-

лебания в соседних точках. Идет процесс распространения колебаний, называемый волной. Теперь смещение ψ (t, x) является функцией двух перемен-

ных: времени и координаты. Линия, вдоль которой распространяются колебания, называется лучом волны. Пусть волна распространяется вдоль оси х.

v				Колебания в точке х = 0:
0				ψ (t, x = 0) = A cos(ω t + ϕ 0 ) .
	x		x

Колебания в точках х > 0 отстают по фазе от колебаний в предыдущих точках. В момент времени t фаза колебаний в точке х меньше на величину, соот-

ветствующую времени t = x . Таким образом, колебания в точке х имеют

v

вид:

		x
ψ (t, x) = A cos ω t −			+ ϕ	.
		v		0

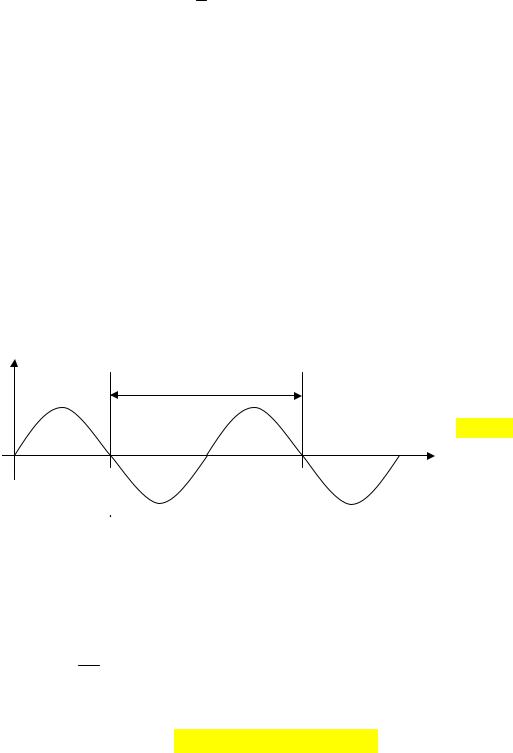
Это и есть уравнение плоской волны, распространяющейся вдоль оси х. Волна называется плоской, потому что фронт этой волны представляет собой плоскость, перпендикулярную оси х. На рисунке ниже изображена волна в некоторый момент времени.

Расстояние, которое волна проходит за один период колебаний, назы-

вается длиной волны. Соответственно, длина волны равна произведению скорости волны на период.

ψ

λ

λ = v T .

0

x

Преобразуем фазу колебаний, исключив из ее выражения скорость волны:

ϕ = ω t −

ω x

+ ϕ

= ω t −

ω T x

+ ϕ

= ω t −

2π

x + ϕ

= ω t − k x + ϕ

,

0

0

0

0

v

λ

λ

Величина k = 2π называется волновым числом. Теперь уравнение волны бу-

λ

дет иметь вид

ψ (t, x) = A cos(ω t − k x + ϕ 0 ),

который считается каноническим.

Отметим, что волновой процесс отличается тройственной перио-

дичностью: состояние среды периодически повторяется через каждые 2π

по фазе, через каждый период во времени и через каждую длину волны в пространстве.

ПЛОСКАЯ ЭЛЕКТРОМАГНИТНАЯ ВОЛНА В ВАКУУМЕ

y Пусть в плоскости

i		y0z	идет переменный элек-
	E
		трический ток в направле-
0		нии	оси 0y, меняющийся
z		по закону
	c		i = I cosω t .
		Во	всем остальном про-
B	x

странстве нет ни зарядов, ни токов.

Переменный ток вдоль оси 0y породит в пространстве переменное магнитное поле, направленное вдоль оси 0z, также изменяющееся по гармоническому закону. Переменное магнитное поле породит в пространстве электрическое поле, направленное вдоль оси 0y, которое также будет изменяться по гармоническому закону. Переменное электрическое поле в свою очередь породит переменное магнитное поле и так далее. Вспомним, что производная от косинуса есть минус синус, а от синуса – косинус, то есть все время получаются гармонические функции.

Таким образом, порождая друг друга, переменные электрическое и магнитное поля будут распространяться вдоль оси 0х в виде плоской электромагнитной волны. Во всех точках плоскости, перпендикулярной оси 0х, колебания вектора Е напряженности электрического поля и вектора В индукции магнитного поля происходят в одинаковой фазе:

r r

E = Emax
r		r
	=	Bmax
B

cos(ω t − k x). cos(ω t − k x)

Эти формулы получены при решении системы уравнений Максвелла, причем скорость этой плоской электромагнитной волны получается равной

с = 3·108 м/c,

то есть равной скорости видимого света в вакууме. Это обстоятельство и навело Максвелла на мысль, что видимый свет есть не что иное, как электромагнитная волна.

Скорость с электромагнитной волны равна произведению длины волны на частоту:

c = λ ν .

Таким образом, длина электромагнитной волны и ее частота обратно про-

порциональны друг другу.

Физики часто называют электромагнитную волну светом. Диапазон частот электромагнитных волн огромен. Ощущение видимого света вызывают электромагнитные волны с частотами примерно от 4·1014 до 8·1014 Гц.

ПЕРЕНОС ЭНЕРГИИ ВОЛНОЙ. ИНТЕНСИВНОСТЬ ВОЛНЫ Распространяющиеся колебания частиц вещества внутри вещества на-

зываются механическими или звуковыми волнами. Распространение переменного электромагнитного поля называется электромагнитной волной. Од-

нако ни механические, ни электромагнитные волны не сопровождаются переносом самого вещества и не связаны с переносом массы. В волне от точки к точке происходит перенос энергии без переноса массы.

В незатухающей волне передается энергия, равная максимальной потенциальной энергии колебаний, пропорциональной квадрату амплитуды волны. Энергия, переносимая волной в единицу времени, называется потоком энергии. Поверхностная плотность потока энергии I называется интенсивностью волны:

I =	dE		,	Вт	.
	dt	S		м2

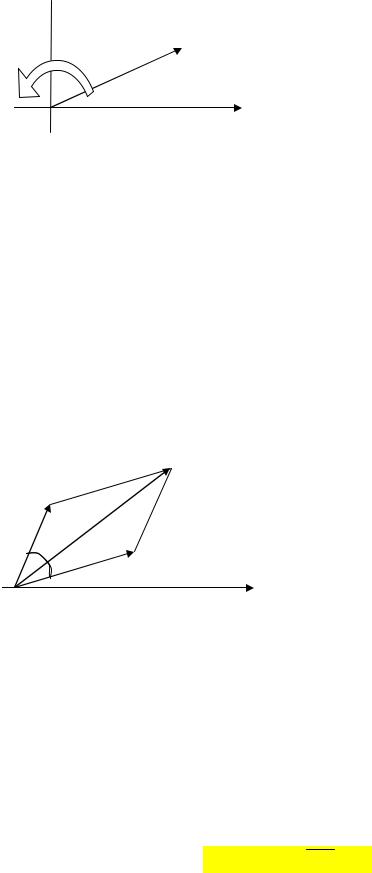
СЛОЖЕНИЕ КОЛЕБАНИЙ

Гармоническое колебание

	A		ψ = Аcos(ω t + ϕ 0 )
			можно изобразить с помощью век-
ω	φ0		торной диаграммы, изображенной
0		ψ	на рисунке слева. Вектор А распо-
			ложен под углом φ0 к оси 0ψ.

Если представить, что вектор А вращается с угловой скоростью ω, как это показано на рисунке, то проекция вектора на ось 0ψ будет равна значениям функции ψ(t).

С помощью векторной диаграммы можно произвести сложение двух колебаний одинакового направления и одной и той же частоты:

ψ = ψ 1 +ψ 2 = A1 cos(ω t + ϕ 01 )+ A2 cos(ω t + ϕ 02 ).

Сумма двух этих колебаний

		А2	А		должна иметь вид
						ψ = A cos(ω t + ϕ 0 ) .
		δ			Амплитуда А будет равна сумме
			А1		векторов А1 и А2:
						r r r
0			ψ			А = А1 + А2 .
Величину вектора А найдем с помощью теоремы косинусов:
			A2 = A2	+ A2	+ 2 A A cos δ ,
			1	2	1	2
где δ = ϕ 02 − ϕ 01			– сдвиг колебаний по фазе.

Теперь можно получить выражение для интенсивности результата сложения двух колебаний. Поскольку интенсивность прямо пропорциональна квадрату амплитуды, получим:

I = I1 + I 2 + 2I1 I 2 cosδ .

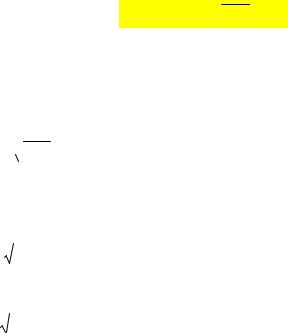
Таким образом, интенсивность результата сложения колебаний зависит от сдвига этих колебаний по фазе.

ИНТЕРФЕРЕНЦИЯ ВОЛН Пусть два луча приходят в одну точку пространства. Тогда в этой точке

происходит сложение колебаний. Если две волны имеют одинаковую частоту, и если сдвиг по фазе между переносимыми этими волнами колебаниями не меняется с течением времени, то эти волны называются когерентными. При попадании лучей когерентных волн в одну точку происходит интерференция этих волн.

Интерференция волн – это сложение когерентных волн, приводящее к их взаимному усилению или гашению. Причиной интерференции является зависимость результата сложения колебаний от их сдвига по фазе. Вернемся к формуле для интенсивности результата сложения колебаний:

I= I1 + I 2 + 2I1 I 2 cosδ

иобратим внимание на то, что I ≠ I1 + I 2 , то есть интенсивность результата

сложения не равна сумме интенсивностей двух приходящих в одну точку лучей. Равенство нарушается из-за присутствия в правой части интерференци-

онного члена 2I1 I 2 cosδ . Поскольку cosδ может принимать все значения от 1

до –1, интенсивность результата сложения колебаний принимает значения от максимального

I max	= I1 + I 2 + 2		I1 I 2		при δ max	= 2πm (максимум интерференции)
до минимального
					при δ min	= π (2m + 1) (минимум интерференции)
	= I1 + I 2 − 2
I min		I1 I 2

где m – любое целое число.

Если волны не когерентные, интерференция отсутствует. Покажем это. Чтобы зарегистрировать интерференцию, необходимо наблюдать процесс сложения в течение некоторого времени, по крайней мере, большего, чем период колебаний. Но за это время сдвиг по фазе может хаотически меняться, и