
- •Курс лекций
- •По дискретной математике
- •(2 Семестр)
- •(Для студентов специальности «Прикладная математика», «Компьютерные системы и сети»)
- •Комбинаторика.
- •§1. Правила комбинаторики. Основные комбинаторные формулы.
- •Размещения.
- •Перестановки.
- •Сочетания.
- •§2. Свойства сочетаний. Бином Ньютона.
- •§3. Числа Фибоначчи. Рекуррентные соотношения.
- •§3. Производящие функции.
- •Теория графов. Введение
- •§1. Основные понятия и определения теории графов.
- •§2. Задачи, послужившие основой теории графов.
- •1. Задача о кенигсбергских мостах.
- •2. Задача о четырех красках.
- •§3. Алгоритмические задачи.
- •1. Задачи о кратчайших путях.
- •Алгоритм решения.
- •Обоснование алгоритма.
- •2. Алгоритм построения Эйлерова цикла.
- •Обоснование алгоритма.
- •3. Потоки на транспортных сетях.
- •Алгоритм Форда - Фалкерсона для нахождения потока наибольшей величины.
- •Обоснование алгоритма.
- •§4. Цикломатическое число графа. Деревья.
- •§5. Эйлерова характеристика. Плоские графы.
- •§6. Теорема о пяти красках.
- •Оценка хроматического числа плоского графа.
- •§7. Графы правильных многогранников.
- •Теория конечных автоматов Введение.
- •§1. Определение автомата Мили. Автомат Мура.
- •§2. Покрытие и эквивалентность. Морфизмы.
- •§3. Эквивалентные состояния автоматов.
- •§4. Процедура минимизации конечных автоматов.
- •§5. Машина Тьюринга.
- •§6. Не полностью описанные автоматы.
- •Алгоритмы и рекурсивные функции. Введение.
- •§1. Основные понятия и определения.
- •§2. Примитивно рекурсивные функции.
- •§3. Частично рекурсивные функции.
- •§4. Машины Тьюринга.
- •Список литературы.
- •2 Семестр
Алгоритм Форда - Фалкерсона для нахождения потока наибольшей величины.
1°.
Перенумеровать произвольным образом
вершины сети
![]() ,
отличные от входа
,
отличные от входа![]() и выхода
и выхода![]() .
.
2°.
Построить произвольный поток
![]() на транспортной сети
на транспортной сети![]() (например, положить
(например, положить![]() ).
).
3°.
Просмотреть пути, соединяющие вход сети
![]() c
выходом
c
выходом
![]() .
Если поток
.
Если поток
![]() полный, то перейти к пункту 4°. В противном
случае рассмотреть путь
полный, то перейти к пункту 4°. В противном
случае рассмотреть путь![]() ,
соединяющий
,
соединяющий![]() с
с![]() ,
все дуги которого не насыщены. Построить
новый поток
,
все дуги которого не насыщены. Построить
новый поток
![]() :
:
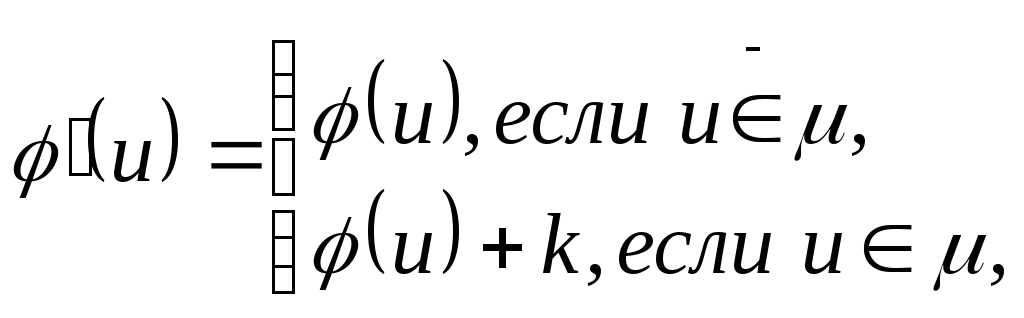
где
![]() .
Повторить этот процесс до получения
полного потока
.
Повторить этот процесс до получения
полного потока![]() .
.
4°.
Присвоить целочисленные метки вершинам
сети
![]() и знаки «+» или «-» дугам по следующим
правилам:
и знаки «+» или «-» дугам по следующим
правилам:
а) входу
![]() присвоить метку 0;
присвоить метку 0;
б) если вершина
![]() получила некоторую метку, а
получила некоторую метку, а![]() —
еще непомеченная вершина, то вершине
—
еще непомеченная вершина, то вершине
![]() ,
такой что
,
такой что![]() присвоить метку
присвоить метку
![]() ,
а дуге
,
а дуге![]() —
знак «+»; вершине
—
знак «+»; вершине
![]() ,
такой что
,
такой что![]() ,
присвоить метку
,
присвоить метку![]() ,
а дуге
,
а дуге![]() —
знак «-». Остальные непомеченные вершины
и дуги метки и знака не получают;
—
знак «-». Остальные непомеченные вершины
и дуги метки и знака не получают;
в) повторить
процесс, описанный в пункте 4°б)
до тех пор, пока не прекратится появление
новых отмеченных вершин и дуг. Если в
результате процесса 4°б)
вершина
![]() не получит метки, то поток обладает
наибольшей величиной. В противном случае
перейти к пункту5°.
не получит метки, то поток обладает
наибольшей величиной. В противном случае
перейти к пункту5°.
5°.
Рассмотреть последовательность
отмеченных вершин
![]() ,
каждая из которых имеет метку, равную
номеру последующей вершины, и
последовательность дуг
,
каждая из которых имеет метку, равную
номеру последующей вершины, и
последовательность дуг![]() и (не обязательно путь), соединяющих
последовательные вершины из
и (не обязательно путь), соединяющих
последовательные вершины из![]() .
Построить новый поток
.
Построить новый поток![]() :
:

Перейти к пункту 4°.
2. Соотношение между величиной потока и пропускной способностью разреза сети.
Введем новые понятия теории транспортных сетей.
Определение
4: Пусть
множество
![]() - такое множество вершин графа, что
- такое множество вершин графа, что![]() .
Множество
.
Множество![]() дуг, заходящих в
дуг, заходящих в![]() ,
т. е. соединяющих вершины
,
т. е. соединяющих вершины![]() с вершинами
с вершинами![]() ,
называетсяразрезом
сети
,
называетсяразрезом
сети
![]() .
.
Определение
5: Пропускной
способностью
![]() разреза
разреза
![]() называется сумма пропускных способностей
дуг, входящих в разрез, т. е.
называется сумма пропускных способностей
дуг, входящих в разрез, т. е.
![]() .
.
Лемма:
Для любого потока
![]() и любого разреза
и любого разреза
![]() справедливо соотношение:
справедливо соотношение:
![]() .
.
Доказательство:
В силу того, что выход сети
![]() ,
для величины потока
,
для величины потока![]() справедливы соотношения:
справедливы соотношения:
![]() .
.
Следствие:
Если для некоторого потока
![]() и некоторого разреза
и некоторого разреза
![]() выполняется равенство
выполняется равенство
![]() ,
то поток
,
то поток![]() обладает наибольшей величиной.
обладает наибольшей величиной.
Лемма и следствие необходимы для обоснования рассмотренного алгоритма.
Обоснование алгоритма.
Прежде всего,
заметим, что реализация алгоритма
состоит из конечного числа шагов. В
самом деле, п. 3°
может применяться лишь конечное число
раз, так как на каждом шаге величина
потока увеличивается, по крайней мере,
на единицу. Вместе с тем величина любого
потока не может превзойти суммарной
пропускной способности дуг, инцидентных
выходу сети
![]() .
.
Процесс присвоения
меток в силу того, что каждый раз получают
метку еще неотмеченные вершины, конечен.
И, наконец, в п. 5°
поток
![]() обладает большей величиной, чем
обладает большей величиной, чем![]() .
Это вытекает из того, что по определению
вершины
.
Это вытекает из того, что по определению
вершины![]() и правил п.4°б)
дугам, входящим в
и правил п.4°б)
дугам, входящим в
![]() ,
может быть присвоен только знак «+».
,
может быть присвоен только знак «+».
Получаемая по
правилу 3°
функция
![]() — поток. Это непосредственно следует
из того, что
— поток. Это непосредственно следует
из того, что![]() — путь. В соответствии с правилом п.5°
строится также поток. Чтобы доказать
это утверждение, рассмотрим три соседние
вершины последовательности
— путь. В соответствии с правилом п.5°
строится также поток. Чтобы доказать
это утверждение, рассмотрим три соседние
вершины последовательности
![]() .
В силу правила4°б)
возможны только ситуации, представленные
на рис. 10. Но в этих ситуациях
.
В силу правила4°б)
возможны только ситуации, представленные
на рис. 10. Но в этих ситуациях
![]() — поток.
— поток.
Пусть процесс,
описанный в п. 4°б),
приводит к тому, что вершина
![]() не получает метки. Обозначим через
не получает метки. Обозначим через![]() множество непомеченных вершин. В силу
того, что
множество непомеченных вершин. В силу
того, что![]() ,
множество
,
множество![]() определяет разрез сети
определяет разрез сети![]() .
Каждая дуга
.
Каждая дуга![]() соединяет помеченную вершину
соединяет помеченную вершину![]() с непомеченной вершиной
с непомеченной вершиной![]() .
Вершина
.
Вершина![]() может остаться непомеченной при условии,
что
может остаться непомеченной при условии,
что![]() .
Аналогично, на каждой дуге
.
Аналогично, на каждой дуге![]() (выходящей из
(выходящей из![]() )
выполняется равенство
)
выполняется равенство![]() ,
поэтому справедливы соотношения:
,
поэтому справедливы соотношения:
![]() .
.
В силу леммы это
означает, что поток
![]() обладает наибольшей величиной.
обладает наибольшей величиной.
Рис. 10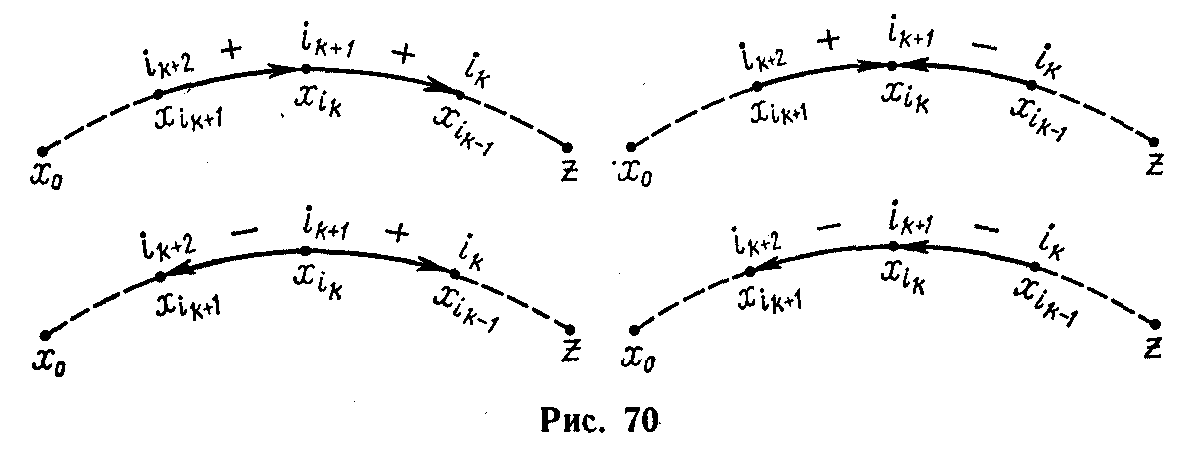
Проведенное рассуждение совместно с леммой составляют доказательство следующей теоремы.
Теорема 1: Для
заданной транспортной сети величина
наибольшего потока равна наименьшей
пропускной способности разрезов, т. е.
![]() .
.
Рис. 11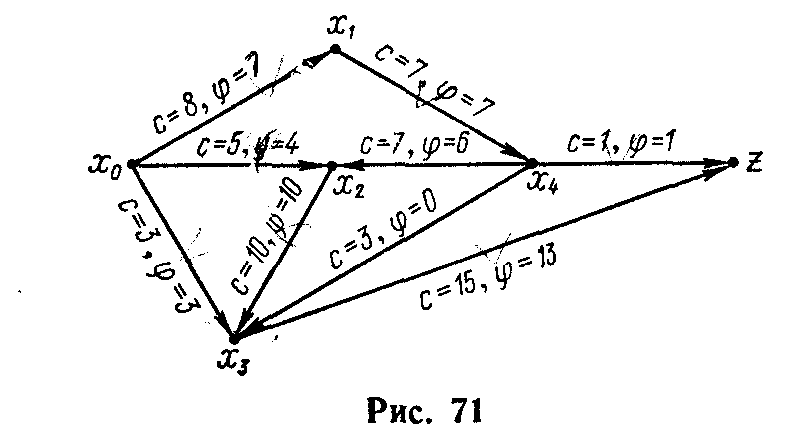
В качестве примера
применения алгоритма Форда - Фалкерсона
рассмотрим транспортную сеть
![]() и полный поток
и полный поток![]() ,
для которого
,
для которого![]() (рис. 11). Применяя правила4°
и 5°
алгоритма, можно получить поток с
величиной
(рис. 11). Применяя правила4°
и 5°
алгоритма, можно получить поток с
величиной
![]() .
.
3. Задача о назначении на должность (комбинаторная прикладная задача).
Пусть в некотором
учреждении имеется 6 вакантных должностей
![]() и 6 работников
и 6 работников![]() .
.
Рис. 12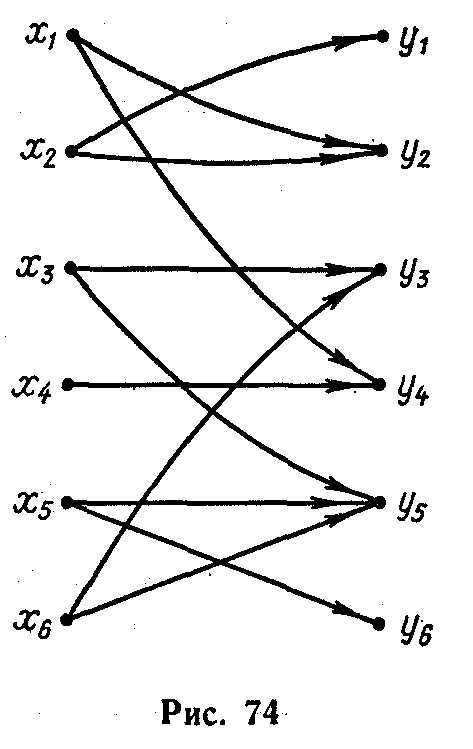
Граф
![]() ,
изображенный на рис. 12, иллюстрирует,
какие должности
,
изображенный на рис. 12, иллюстрирует,
какие должности![]() может в силу своей квалификации занимать
работник
может в силу своей квалификации занимать
работник![]() .
Пусть выполнено условие: каждый работник
может занимать хотя бы одну должность
и на каждую должность претендует хотя
бы один работник. Можно ли произвести
назначение на должности так, чтобы все
шесть должностей заняли работники
соответствующей квалификации?
.
Пусть выполнено условие: каждый работник
может занимать хотя бы одну должность
и на каждую должность претендует хотя
бы один работник. Можно ли произвести
назначение на должности так, чтобы все
шесть должностей заняли работники
соответствующей квалификации?
Один из способов
решения этой задачи состоит в рассмотрении
вспомогательной транспортной сети
![]() .
Для ее получения добавим к множеству
.
Для ее получения добавим к множеству![]() вершин графа
вершин графа
![]() еще две вершины: вход
еще две вершины: вход
![]() и выход
и выход![]() .
Соединим
.
Соединим![]() с каждой вершиной
с каждой вершиной
![]() дугой пропускной способности
дугой пропускной способности
![]() и каждую вершину
и каждую вершину![]() с
с![]() дугой пропускной способности
дугой пропускной способности![]() .
Припишем дугам исходного графа
.
Припишем дугам исходного графа![]() бесконечные пропускные способности.
Получим транспортную сеть
бесконечные пропускные способности.
Получим транспортную сеть![]() ,
изображенную на рис. 13.
,
изображенную на рис. 13.
Рис. 13
Ясно, что если на
сети
![]() будет существовать поток такой, что
будет существовать поток такой, что![]() ,
то есть поток, насыщающий выходные дуги
(одновременно он будет насыщать и входные
дуги
,
то есть поток, насыщающий выходные дуги
(одновременно он будет насыщать и входные
дуги![]() ),
то требуемое назначение будет возможно
произвести. Нужно назначить работника
),
то требуемое назначение будет возможно
произвести. Нужно назначить работника![]() на должность
на должность![]() в том и только том случае, когда
в том и только том случае, когда![]() .
.
