Сочетания.

1) Сочетания без повторений.

Определение 3: Сочетания из элементов поэлементов () – это расстановки, отличающиеся друг от другасоставом, но не порядком элементов. Обозначают: .

Теорема 4: Число сочетаний находится по следующей формуле:

.

Доказательство: .

Следствие: Выведенная формула совпадает с формулой для числа повторений из элементов одного типа иэлементов второго типа:

.

Иными словами справедливо равенство: .

Примеры: Выбор делегации, число призеров в соревновании и т. д.

Замечание: , .

Существенное отличие числа сочетаний от числа соответствующих размещений состоит в том, что для размещений важен состав и порядок элементов в подмножествах, а для сочетаний важен только состав.

2) Сочетания с повторениями.

Пусть имеется предметы различных типов. Сколькокомбинаций можно сделать из них, если не принимать во внимание порядок элементов? Эту задачу в общем виде можно решать точно так же, как задачу с пирожными.

Задача: В кондитерском магазине продаются пирожные 4 сортов: наполеон, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?

Зашифруем каждую покупку с помощью нулей и единиц. Напишем столько единиц, сколько куплено наполеонов, затем пишем 0, чтобы отделить пирожные одного типа от другого и т.д. Тогда каждой покупке будет соответствовать последовательность из семи единиц и трех нулей в различном порядке. Число всех таких покупок тогда будет равно:

.

Для числа сочетаний с повторениями существует формула:

.

§2. Свойства сочетаний. Бином Ньютона.

Одной из наиболее распространённых комбинаторных формул является формула числа сочетаний. Для упрощения подсчётов и для доказательства некоторых утверждений удобно использовать следующие свойства сочетаний:

1. .

2. .

Доказательство:

1) .

2) .

Сочетания можно встретить и в школьном курсе математики. Например, в качестве коэффициентов бинома Ньютона выступают именно сочетания. Формула бинома Ньютона в общем виде и её доказательство приводятся в следующей теореме.

Теорема 1: .

Доказательство: Применим индукцию по .

При :.

Пусть формула верна, для случая, когда . В этом случае следующее равенство будем считать выполненным:

.

Покажем, что формула выполняется для - й степени:

.

В доказательстве можно также использовать свойство: .

Следствие: Рассмотрим некоторые частные случаи формулы бинома Ньютона:

1) если , то.

2) если , то.

Определение 1: Коэффициенты бинома Ньютонаназываются биномиальными коэффициентами.

Числовые значения биномиальных коэффициентов вычисляются по формуле числа сочетаний: . Готовые значения этих коэффициентов располагаются в строкахтреугольника Паскаля.

1 n = 0

1 1 n = 1

1 2 1 n = 2

1 3 3 1 n = 3

1 4 6 4 1 n = 4

1 5 10 10 5 1 n = 5

. . . . . . . . . . . . . . . . . . . . . . . . .

Треугольник Паскаля строится следующим образом. Боковые стороны состоят из единиц. Числа, находящиеся внутри, являются суммой вышестоящих чисел. Каждая строка треугольника соответствует некоторой степени для суммы и содержит соответствующие биномиальные коэффициенты. Таким образом, для того, чтобы раскрыть степень суммы, нужно из треугольника Паскаля взять строку, соответствующую данной степени. Эта строка будет содержать нужные коэффициенты, к которым приписываются соответствующие буквенные выражения. Можно заметить, что строки треугольника Паскаля симметричны, поэтому достаточно взять только половину биномиальных коэффициентов и, если нужно, средний элемент.

Формула бинома Ньютона применяется, когда нужно возвести в целую степень сумму двух слагаемых. Если же это требуется произвести для суммы трёх и более слагаемых, тогда применяют полиномиальную формулу:

Сумма в правой части формулы строится по аналогии с формулой бинома. Она представляет собой сумму слагаемых, состоящих из коэффициента и буквенной части. Сумма этих слагаемых берется по всевозможным разбиениям числанацелых неотрицательных слагаемых, при этом коэффициент находится по формуле числа перестановок с повторениями:

.

Если числа получаются перестановкой из чисел, то считается, что

.

Пример: Возвести в пятую степень сумму трёх слагаемых.

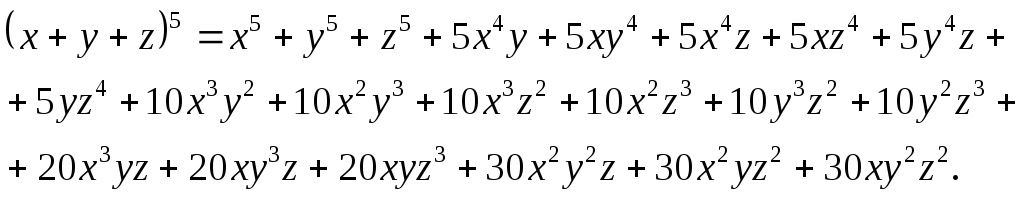
Здесь учитывается, что 5 можно разбить на 3 слагаемых пятью способами:

;;;;.

Тогда для каждого такого разбиения известны числа ,. Значит, все коэффициенты можно для каждого случая найти по формуле:

.

Полученные коэффициенты: ,,,,. Буквенная часть также формируется в связи с разложениями числа 5 на 3 слагаемых. Таким образом, получается разложение, приведённое выше.

Замечание: Сумма полиномиальных коэффициентов может быть найдена по формуле:

.

Для коэффициентов из рассмотренного примера можно проверить:

,

.

Рассмотрим - сочетания с повторениями, составленные из элементовтипа, например избуквы. Число таких сочетаний равно:. Разобьём все эти сочетания на классы, отнеся к‑ му классу сочетания, в которыхраз входит буква. Остальныемест могут быть заняты оставшимися буквами, число которых равно. Поэтому в- й класс входит столько сочетаний, сколько можно составитьсочетаний с повторениями из элементовтипов, т.е..

Значит общее число всех таких сочетаний равно:

, т.е.

.

Меняя теперь наинаи используя равенство, получаем зависимость между биномиальными коэффициентами:

.

Доказать эту формулу можно методом математической индукции по числу слагаемых в правой части. Используя эту зависимость, можно получить формулы для подсчёта суммы чисел натурального ряда от 1 до (при), суммы квадратов натуральных чисел (при), сумму кубов (при).

Если , то искомая зависимость имеет вид:

.

Для имеем:

,

или окончательно:

.

Для получаем:

,

или после преобразований:

.

Таким образом, можно получить формулы для сумм более высоких степеней натуральных чисел.