
- •Курс лекций
- •По дискретной математике
- •(2 Семестр)
- •(Для студентов специальности «Прикладная математика», «Компьютерные системы и сети»)
- •Комбинаторика.
- •§1. Правила комбинаторики. Основные комбинаторные формулы.
- •Размещения.
- •Перестановки.
- •Сочетания.
- •§2. Свойства сочетаний. Бином Ньютона.
- •§3. Числа Фибоначчи. Рекуррентные соотношения.
- •§3. Производящие функции.
- •Теория графов. Введение
- •§1. Основные понятия и определения теории графов.
- •§2. Задачи, послужившие основой теории графов.
- •1. Задача о кенигсбергских мостах.
- •2. Задача о четырех красках.
- •§3. Алгоритмические задачи.
- •1. Задачи о кратчайших путях.
- •Алгоритм решения.
- •Обоснование алгоритма.
- •2. Алгоритм построения Эйлерова цикла.
- •Обоснование алгоритма.
- •3. Потоки на транспортных сетях.
- •Алгоритм Форда - Фалкерсона для нахождения потока наибольшей величины.
- •Обоснование алгоритма.
- •§4. Цикломатическое число графа. Деревья.
- •§5. Эйлерова характеристика. Плоские графы.
- •§6. Теорема о пяти красках.
- •Оценка хроматического числа плоского графа.
- •§7. Графы правильных многогранников.
- •Теория конечных автоматов Введение.
- •§1. Определение автомата Мили. Автомат Мура.
- •§2. Покрытие и эквивалентность. Морфизмы.
- •§3. Эквивалентные состояния автоматов.
- •§4. Процедура минимизации конечных автоматов.
- •§5. Машина Тьюринга.
- •§6. Не полностью описанные автоматы.
- •Алгоритмы и рекурсивные функции. Введение.
- •§1. Основные понятия и определения.
- •§2. Примитивно рекурсивные функции.
- •§3. Частично рекурсивные функции.
- •§4. Машины Тьюринга.
- •Список литературы.
- •2 Семестр
Обоснование алгоритма.
Докажем, что после
конечного числа применений правила 3°
для каждой дуги графа станет справедливым
неравенство
![]() .
.
Для этого заметим,
что на любом этапе метки
![]() при
при
![]() ,
а метка
,
а метка![]() ,
что можно доказать по индукции. В самом
деле, при первом применении правила3°
будет изменена метка
,
что можно доказать по индукции. В самом
деле, при первом применении правила3°
будет изменена метка
![]() у одной из вершин
у одной из вершин![]() ,
смежных с вершиной
,
смежных с вершиной
![]() .
Эта вершина
.
Эта вершина![]() получит новую метку
получит новую метку
![]() .
.
Предположим, что
после того, как применено правило 3°
![]() раз
раз
![]() ,
станет справедливым утверждение, что
,
станет справедливым утверждение, что
![]() для
для![]() .
На
.
На![]() шаге какая-то вершина
шаге какая-то вершина![]() получит новую метку
получит новую метку![]() .
Но в силу предположения индукции
.
Но в силу предположения индукции![]() ,
кроме того,
,
кроме того,
![]() ;
поэтому
;
поэтому
![]() .
.
Ясно, что при каждом изменении метка вершины графа уменьшается на положительную величину, не меньшую, чем минимальная разность длин путей графа.
Из этих двух утверждений вытекает, что метка-любой вершины графа может изменяться лишь конечное число раз. Так как вершин конечное множество, то правило 3° может применяться лишь конечное число раз.
Докажем теперь
утверждения, содержащиеся в пункте 5°.
Вершина
![]() такая, что
такая, что![]() обязательно найдется в случае, если
существует хотя бы один путь, соединяющий
обязательно найдется в случае, если
существует хотя бы один путь, соединяющий![]() с
вершиной
с
вершиной
![]() .
Ибо тогда, как нетрудно сообразить,
метка
.
Ибо тогда, как нетрудно сообразить,
метка
![]() .
Поэтому
.
Поэтому
![]() —
это, например, та вершина, которая
послужила для изменения метки
—
это, например, та вершина, которая
послужила для изменения метки
![]() в последний раз. Аналогично доказывается
существование вершин
в последний раз. Аналогично доказывается
существование вершин![]() .
.

По условию дуги
графа имеют положительную длину, поэтому
метки
![]() образуют строго убывающую последовательность
неотрицательных чисел, отличающихся
друг от друга на величину, большую или
равную длине кратчайшей дуги графа.
Следовательно, какое-то
образуют строго убывающую последовательность
неотрицательных чисел, отличающихся
друг от друга на величину, большую или
равную длине кратчайшей дуги графа.
Следовательно, какое-то![]() .
(Вершина
.
(Вершина![]() выделена тем, что ей в силу правила2°
с самого начала присвоена метка
выделена тем, что ей в силу правила2°
с самого начала присвоена метка
![]() и в формировании этой метки не участвуют
дуги графа.)
и в формировании этой метки не участвуют
дуги графа.)
Докажем, что путь
![]() — кратчайший. Для этого рассмотрим
произвольный путь:
— кратчайший. Для этого рассмотрим
произвольный путь:![]() ,
соединяющий решину
,
соединяющий решину![]() с
с![]() .
Имеем неравенства:
.
Имеем неравенства:
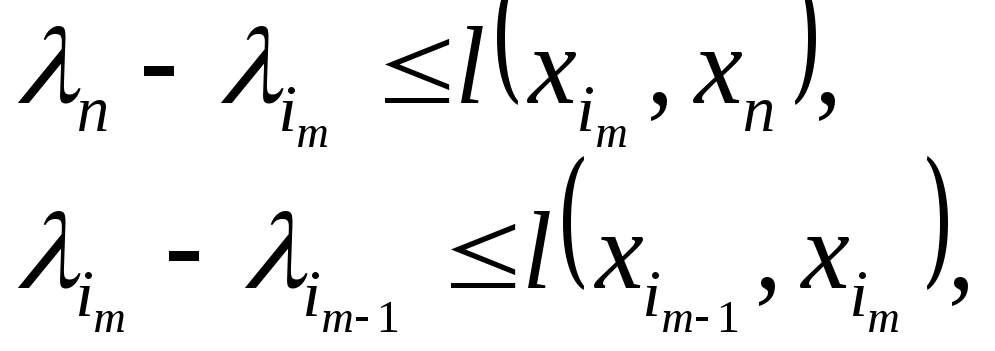
Складывая эти неравенства, получаем соотношение:
![]() ,
,
так как
![]() .
В то же время, по построению пути
.
В то же время, по построению пути![]() имеем:
имеем:
![]() ,
откуда
,
откуда
![]() .
.
Пример.
В графе
![]() (рис. 9) легко установить, что кратчайший
путь, соединяющий вершины
(рис. 9) легко установить, что кратчайший
путь, соединяющий вершины
![]() и
и![]() ,
имеет длину
,
имеет длину
![]() .
.
2. Алгоритм построения Эйлерова цикла.
Обратимся к задаче
об эйлеровом цикле, уже рассмотренной
нами в предыдущем параграфе. Пусть
![]() — связный граф, степени всех вершин
которого — четные числа. Теорема 1 §2
гарантирует существование эйлерова
цикла.
— связный граф, степени всех вершин
которого — четные числа. Теорема 1 §2
гарантирует существование эйлерова
цикла.
Как фактически построить его? Оказывается, что достаточно выполнять следующие правила.
Алгоритм.
1°.
Выбрать произвольно некоторую вершину
![]() .
.
2°.
Выбрать произвольно некоторое ребро
![]() ,
инцидентное
,
инцидентное
![]() ,
и присвоить ему номер 1. (Назовем это
ребро «пройденным».)
,
и присвоить ему номер 1. (Назовем это
ребро «пройденным».)
3°. Каждое пройденное ребро вычеркивать и присваивать ему номер, на единицу больший номера предыдущего вычеркнутого ребра.
4°.
Находясь в вершине![]() ,
не выбирать ребра, соединяющего
,
не выбирать ребра, соединяющего![]() с вершиной
с вершиной
![]() ,
если только есть возможность другого
выбора.
,
если только есть возможность другого
выбора.
5°.
Находясь в вершине
![]() ,
не выбирать ребра, которое является
«перешейком» (при удалении которого
граф, образованный незачеркнутыми
ребрами, распадается на две компоненты
связности, имеющие хотя бы по одному
ребру).
,
не выбирать ребра, которое является
«перешейком» (при удалении которого
граф, образованный незачеркнутыми
ребрами, распадается на две компоненты
связности, имеющие хотя бы по одному
ребру).
6°.
После того, как в графе будут занумерованы
все ребра, цикл
![]() ,
образованный ребрами с номерами от 1 до
,
образованный ребрами с номерами от 1 до![]() ,
где число ребер в графе, есть эйлеров
цикл.
,
где число ребер в графе, есть эйлеров
цикл.
