
- •4. Определенный интеграл с переменным верхним пределом:
- •6. Интегрирование по частям:
- •7. Вычисление площади в декартовой системе координат:
- •12. Несобственные интегралы второго рода:
- •9. Вычисление объема тела вращения:
- •10. Работа переменной силы:
- •11. Несобственные интеграла с бесконечными пределами интегрирования:
- •21. Метод вариации произвольных постоянных:
- •33. Достаточные признаки сравнения:
- •39. Ряды Маклорена для некоторых функций:
- •40. Приложения степенных рядов:
- •53. Нормальное распределение
11. Несобственные интеграла с бесконечными пределами интегрирования:
Пусть
функция f(x)
непрерывна на [a,+∞]
, тогда по определению полагают: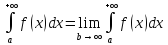 несобственный
интеграл первого рода.
несобственный
интеграл первого рода.
Если существует конечные предел в * то говорят, что Н.И. сходится, если предел не существует или бесконечен – интеграл называется расходящимся.
Для исследования сходимости:
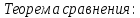 если на промежутке
[a,+∞)
непрерывные функции f(x),
ϕ(x)
удовлетворяющие условию 0≤f(x)≤ϕ(x),то
из сходимости интеграла
если на промежутке
[a,+∞)
непрерывные функции f(x),
ϕ(x)
удовлетворяющие условию 0≤f(x)≤ϕ(x),то
из сходимости интеграла
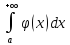 следует
сходимость
интеграла
следует
сходимость
интеграла
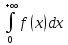 ,
а из расходимости
,
а из расходимости
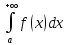 следует
расходимость
следует
расходимость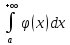 .
.
Предельный
признак сходимости: если
существует предел
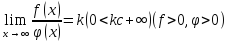 ,то
несобственные интегралы
,то
несобственные интегралы
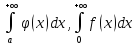 ,
либо оба сходятся либо оба расходятся.
,
либо оба сходятся либо оба расходятся.
Теорема
3: из сходимости
интеграла
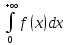 ,
следует сходимость интеграла
,
следует сходимость интеграла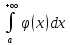 .
.
13. Уравнение связывающее независимую переменную, искомую функцию и ее производные называется дифференциальным уравнением (ДУ).
Решением ДУ называется функция которая при подстановке в уравнение обращают его в тождество.
Общим решением ДУ первого порядка называется функция у=ϕ(х,с), содержащее одну произвольную постоянную и удовлетворяющая следующим условиям:1). Она является решением ДУ при каждом фиксируемом значении С. 2). Каково бы ни было начальное условие y(x0)=y0 найдется такое значение произвольной постоянной с=С0, что функция у=ϕ(х,с0) будет удовлетворять заданному начальному условию.
Частным решение ДУ первого порядка называют любую функцию у=ϕ(х,с0) полученную из ОР при конкретных значениях постоянной.
Теорема: Если функция f(x,y) м ее частная производная f’(x,y) непрерывны в некоторой области Д содержащей точку(х0,у0), то существует единственное решение у=у(х) ДУ y’=f(x,y) удовлетворяющее начальному условию.
17. 1-ый тип: уравнения не содержащие явно искомую функцию у: F(x,y’,y’’)=0. Уравнение допускает понижение порядка(т.е. сводится к уравнению более низкого порядка – к первому) с помощью замены y’=z(x), где z(x)-новая неизвестная функция, тогда y’’=z’ и уравнение примет вид F(x,z,z’),решая его находим функцию z(x)=ϕ(x,C1), в итоге искомая функция у находится интегрированием:

2-ой тип: уравнение не содержащее явно независимую переменную х: F(y,y’,y’’)=0. Примени метод понижения порядка, сделаем замену: y’=p(y) y’’=(p(y))’x=dp/dy*y’x=pdp/dy,уравнение примет вид F(y,p,pdp/dy)=0 - ДУ 1-го порядка, откуда находим функцию p=ϕ(y,C1) или dy/dx=ϕ(y,C1)–с разделяющими переменными (РАЗДЕЛИТЬ ПЕРЕМЕННЫЕ). Du/ϕ(y,C1)=dx. Далее интегрируем.
18. ЛОДУ 2-го порядка: y’’+p(x)y’+q(x)y=0 *
Функции y1(х),y2(х) называются линейно-зависимыми на (а,в), если существуют такие числа α1,α2, из которых хотя бы одно отлично от 0, что выполняется равенство α1y1(х)+α2y2(х)=0 для любых х из интервала (а,в). Если же из выполнения указанного равенства следует, что α1=α2=0, то функции y1(х),y2(х) называются линейно-независимыми на (а,в).
О
линейно-зависимых или независимых
y1(х),y2(х) можно
судить по определителю:
 -вронскиан
(определитель Вронского).
-вронскиан
(определитель Вронского).
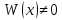 ни
в одной точке (а,в), тогда и только тогда,
когда функции y1(х),y2(х)
линейно-независимы.
ни
в одной точке (а,в), тогда и только тогда,
когда функции y1(х),y2(х)
линейно-независимы.
Теорема: (о структуре ОР ЛОДУ 2-го порядка) если y1(х) и y2(х) линейно-независимые решения уравнения (*), то функция y=C1*y1(x)+C2*y2(x)-где С1,С2 – произвольные постоянные являющиеся общим решением уравнения (*).
19. ЛОДУ 2-го порядка с постоянными коэффициентами: y’’+py’+qy=0
1.
Д˃0
к1≠к2
к1,к2=(-p+(-)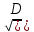 /2a
(
/2a
(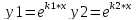 )
ОР (y=C1ek1x+C2ek2x)
)
ОР (y=C1ek1x+C2ek2x)
2. Д=0 к1=к2=к к=-p/2 (y1=ekx y2=ekxx) OP (y=C1ekx+C2ekxx)
3.
Д˂0
Д=-р-4q˂0
k1,k2=(-p+(-)i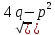 /2=α+(-)βi
/2=α+(-)βi
OP (y=C1eαxcos(βx)+C2eαxsin(βx)=eαx(C1cos(βx)+C2sin(βx))
20. ЛНДУ 2-го порядка: y’’+py’+qy=f(x)
Теорема( о структуре ОР ЛНДУ 2-го порядка) общим решением ЛНДУ является сумма общего решения однородного уравнения соответствующее y’’+py’+qy=f(x) и некоторого частичного решения уравнения y’’+py’+qy=f(x): yон=уоо+учн
