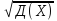- •4. Определенный интеграл с переменным верхним пределом:
- •6. Интегрирование по частям:
- •7. Вычисление площади в декартовой системе координат:
- •12. Несобственные интегралы второго рода:
- •9. Вычисление объема тела вращения:
- •10. Работа переменной силы:
- •11. Несобственные интеграла с бесконечными пределами интегрирования:
- •21. Метод вариации произвольных постоянных:
- •33. Достаточные признаки сравнения:
- •39. Ряды Маклорена для некоторых функций:
- •40. Приложения степенных рядов:
- •53. Нормальное распределение
33. Достаточные признаки сравнения:
1.
Признак сравнения:
пусть даны 2 знака положительных ряда
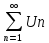 ,
,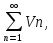 причем начиная с некоторогоn
Un≤Vn,
тогда из сходимости
причем начиная с некоторогоn
Un≤Vn,
тогда из сходимости
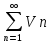 следует сходимость
следует сходимость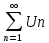 ,
а из расходимости
,
а из расходимости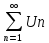 следует расходимость
следует расходимость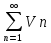 .
.
2.
Предельный признак сравнения: пусть
даны 2 знака положительных ряда
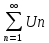 ,
,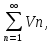 и пусть
и пусть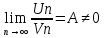 ,
тогда ряды
,
тогда ряды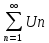 ,
,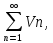 либо оба расходятся, либо оба сходятся.
либо оба расходятся, либо оба сходятся.
3.
Признак Даламбера:
пусть дан знака положительный ряд
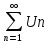 и пусть существует конечный или
бесконечный предел отношения последующего
члена ряда к предыдущему:
и пусть существует конечный или
бесконечный предел отношения последующего
члена ряда к предыдущему: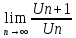 =l
=l
При l˂1 ряд сходится
При l˃1 ряд расходится
При l=1 признак ответа не дает
34. Интегральный признак Коши: если члены знака положительного ряда могут быть представлены, как числовые значения некоторой непрерывной, монотонно убывающей на промежутке [1,∞) функции f(x), так что U1=f(1), U2=f(2) и т.д. , а Un=f(n).
1.
если
 сходится, то сходится ряд
сходится, то сходится ряд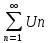
2.
Если
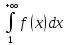 расходится,
то расходится и ряд
расходится,
то расходится и ряд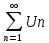
38. Рядом Тейлора
для функции f(x)
называется ряд вида:
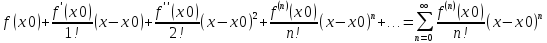
Если
модули всех производных функции f(x)
ограничены в окрестности точки х0 одним
и тем же числом М˃0, то для любых х из
этой окрестности ряд Тейлора функции
f(x)
сходится к самой функции f(x),
т.е. имеет место разложение:
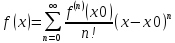 ,причем это разложениеединственно.
,причем это разложениеединственно.
При
х0=0 ряд Тейлора называется рядом
Маклорена
и имеет вид:

39. Ряды Маклорена для некоторых функций:
1).
y=sinx
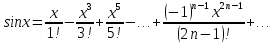
(абсолютно сходится на всей числовой оси)
2).
y=cosx

(абсолютно сходится на всей числовой оси)
3).
y=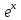
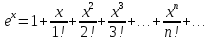
(абсолютно сходится на всей числовой оси)
4). y=ln(1+x)
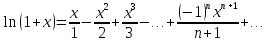
(сходится , если х ϵ (-1,1])
5).
y=(1+x)m
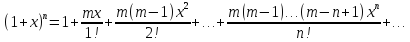
Если m целое, положительное число, то вместо ряда получается конечная сумма.
Если m≥0 ряд сходится при хϵ [-1,1]
-1˂m˂0, то xϵ(-1,1] , m≤1, то xϵ(-1,1)
40. Приложения степенных рядов:
Приближенное вычисление
Пусть требуется вычислить значение функции при х=х1 с заданной точностью ε функция раскладываем в степенной ряд подставляя вместо х, значения х1 и оставляем для вычисления столько членов ряда, сколько необходимо для соблюдения заданной точности ε.
Для знака чередующихся рядов первый из отбрасываемых членов ряда должен быть по модулю меньше заданной точности.
Вычисление интегралов
Отметим, что абсолютно сходящиеся ряды можно дифференцировать и интегрировать почленно, при этом также получаются сходящиеся ряды.
Сперва разлаживаем под интегральную функцию в степенной ряд, затем интегрируем почленно.
Приближенное вычисление ДУ
Запишем разложение в ряд Тейлора решение задачи Коши
43.Теорема(сложение вероятностей для несовместных событий):вероятность суммы 2-ч несовместных событий равна сумме вероятностей этих событий. P(A+B)=P(A)+P(B)
Теорема(сложения вероятностей для произвольных событий): вероятность суммы для произвольных событий равна сумме вероятностей этих событий без вероятности их произведения. P(A+B)=P(A)+P(B)-P(AB)
44. Вероятность события В, при условии, что произошло событие А, называется условной вероятностью события В и обозначается: P(B/A)
Теорема: вероятность произведения двух событий А и В равна произведению вероятности одного из них, на условную вероятность другого в предположении, что первое имеет место: P(AB)=P(A)*P(B/A)
Замечание: вероятность совместного появления 2-х независимых событий равна произведению вероятностей этих событий: P(AB)=P(A)*P(B)
45. Теорема: вероятность события А равна сумме произведений вероятностей всех гипотез на условную вероятность события А: Р(А)=P(H1)*P(A/H1)+..+P(Hn)P(A/Hn)=
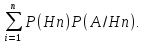
Пусть имеется полная группа событий H1,H2,…,Hn вероятности которых P(H1),P(H2),…,P(Hn) известны до опыта(вероятности априори). Производится опыт (испытание) в результате которого зарегистрировано появление события А. Требуется найти вероятности гипотез после опыта (апостериори). т.е. фактически переоценить вероятности гипотез, т.к. P(AІHi)=P(A)*P(HiІA)=P(Hi)*P(AІHi) – откуда P(HiІA)=(P(Hi)*P(AІHi))/P(A)=(P(Hi)*P(AІHi))/∑P(Hi)*P(AІHi) – формула Байеса.
46. Серия повторений независимых испытаний в каждом из которых некоторое событие А происходило с одной и той же вероятностью р - называется схемой Бернулли. Т.о. в схеме Бернулли для каждого испытания возможны только 2 исхода: 1). Событие А происходит с вероятностью р. 2). Событие А не происходит с вероятностью 1-р=q.
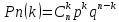 -
Формула Бернулли.
-
Формула Бернулли.
Теорема(Пуассона):пусть
вероятность появления события А в каждом
из n–испытаний
мала (близка к 0), а число испытаний
достаточно велико, тогда вероятность
того, что в испытаний событие Р наступит
к- раз выражает формула
Пуассона:
 где λ=
где λ= (λ≤10).
(λ≤10).
Теоремы Лапласа: 1. пусть вероятность наступления события А в каждом n–независимых испытаний постоянно и равна p(0˂p˂1). Тогда вероятность того, что в –испытаний событие появится к- раз можно найти по приближенной формуле:
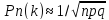 *ϕ(x),
где x=k-np/
*ϕ(x),
где x=k-np/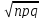 ,
а функция имеет вид ϕ(x)=1/2π*
,
а функция имеет вид ϕ(x)=1/2π*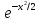 .
.
2.
Интегральная:
пусть вероятность того, что в –испытаний
событие А произойдет не менее к1
и не более к2
раз определяется по формуле:
 ,
где
,
где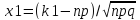 x2
x2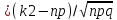 Ф(х)=
Ф(х)=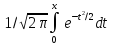 -Функция
Лапласа.
-Функция
Лапласа.
Ф(-х)=-Ф(х)-нечетная, Ф(х)=1/2 для х˃5
49.
ДСВ Х называется распределенной
по биномиальному закону,
если она принимает свои значения к с
вероятностями вычисленными по формуле
Бернулли:
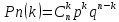
Характеристики:
M(x)=np
; D(x)=npq;
σ=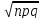
СВ
Х называется распределенной
по закону Пуассона,
если вероятности с которыми она принимает
свои значения вычисляется по формуле
Пуассона:
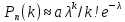
Характеристики:
M(x)=np=λ;
D(x)=np=λ;
σ(x)=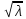
50. Пусть функция распределения непрерывной СВ имеет производную F’(x)=p(x), тогда функция p(x) называется плотностью вероятности непрерывной случайной величины.
Свойства плотности вероятности:
P(x)≥0 (P(x))
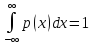
P(a˂x˂b)=
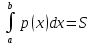
a=-∞ b=x p(-∞˂X˂x)=p(X˂x)=F(x) F(x)=
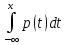
Числовые характеристики непрерывной СВ:
под математическим ожиданием непрерывной СВ Х понимается величина несобственного интеграла:
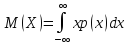 ,
если он сходится.
,
если он сходится.
D(X)=
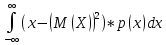
σ(X)=
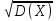
51. Непрерывной
СВ Х называется равномерно
распределенной,
если ее плотность вероятности постоянна
на отрезке [a,b],
а вне этого отрезка =0, т.е. p(x)=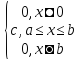
Плотность
вероятности распределения:
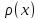 =
=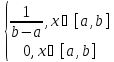
F(x)=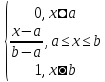
Числовые характеристики:
M(X)=(a+b)/2
D(X)=(b-a)2/12
Σ(X)=Іb-aІ/2
52.
Распределение
непрерывной СВ называется показательным,
если плотность вероятности имеет вид:
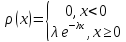 λ≥0
λ≥0
F(x)=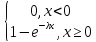
Числовые характеристики:
M(X)=1/λ
D(X)=1/λ^2
σ(X)=1/λ
14. ДУ первого порядка с разделяющими переменными: P1(x)Q1(y)dx+P2(x)Q2(y)dy=0
При делении на Q1(y)P2(x) могут быть потеряны решения, если отдельно решить уравнение Q1(y)P2(x)=0 можно установить так называемые особые решения, которые могут быть получены из общего решения.
Уравнение вида y’=f1(x)f2(y) также называется ДУ с разделяющими переменными.
15. Функция f(x,y) называется однородной функцией н-ной степени, если при умножении каждого ее фрагмента на t вся функция умножается на tn: f(tx,ty)=tn*f(x,y). Функция называется однородной в нулевой степени, если f(tx,ty)=f(x,y).
ДУ 1-го порядка y’=f(x,y) называется однородным, если функция f(x,y) стоящая справа является однородной функцией нулевой степени.
Можно показать, что любое однородное уравнение сводится к уравнению вида: y’=ϕ(y/x) (*).
Полагая (y/x=u) где u, новая независимая функция сводят однородное уравнение (*) к уравнению с разделяющими переменными.
16. Уравнения вида y’+p(x)y=q(x) заданные непрерывной функцией называются линейными ДУ 1-го порядка.
Метод решения: искомая функция у представляется в виде произведения 2-х новых функций u и v: y=uv, тогда y’=u’v+uv’
u’v+uv’+p(x)uv=q(x)
u’v+u(v’+p(x)v)=q(x)
потребуем, чтобы выражение в скобке
обращалось в ноль, приходим к системе: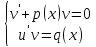
Сначала из 1-го уравнения системы находят функцию v=v(x) это уравнение с разделяющими переменными: v’+p(x)*v=0
v’=-p(x)*v
dv/dx=-p(x)*v
dv/v=-p(x)dx
Ln|v|=-
V=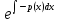
Во второе уравнение системы подставляют v находим функцию u=u(x,C) , обычно эта функция находится непосредственным интегрированием. В итоге y=u(x,C)*v(x)- ОР исходного уравнения.
Уравнение Бернулли: y’+p(x)y=q(x)yα
17. ДУ 2-го порядка, допускающие понижение порядка: 1-ый тип: F(x,y’,y’’)=0 (т.е. сводится к уравнению более низкого порядка) с помощью замены y’=z(x) где z-новая независимая функция, тогда: y’’=z’ и уравнение
32. Рядом
называется выражение вида:
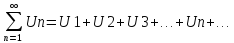 Un
– общий член ряда.
Определение:
если существует конечный предел
последовательности частичных сумм ряда
при n→∞,
то ряд
Un
– общий член ряда.
Определение:
если существует конечный предел
последовательности частичных сумм ряда
при n→∞,
то ряд
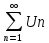 – называетсясходящимся,
при этом её сумма равна пределу частичных
сумм.
– называетсясходящимся,
при этом её сумма равна пределу частичных
сумм.
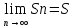 - сумма ряда.
Если же предел последовательных
частичных сумм не существует или
бесконечен,ряд
называется расходящимся.
Свойства:
1.
Если ряд
- сумма ряда.
Если же предел последовательных
частичных сумм не существует или
бесконечен,ряд
называется расходящимся.
Свойства:
1.
Если ряд
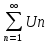 сходится и С ≠ 0 – некоторая постоянная,
то сходится и ряд
сходится и С ≠ 0 – некоторая постоянная,
то сходится и ряд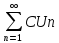 ,
причем его сумма = СS,
где S
=
,
причем его сумма = СS,
где S
=
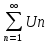 .
.
2.
Если ряды
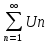 сходятся, причем сумма
сходятся, причем сумма
Un
= S1,
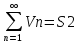 ,
то сходится и ряды
,
то сходится и ряды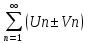 ,
причем
,
причем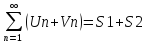 ,
,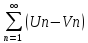 =S1-S2.
Теорема:
если ряд сходится, то предел общего
члена ряда равен 0:
=S1-S2.
Теорема:
если ряд сходится, то предел общего
члена ряда равен 0:
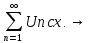

35.
Признак Лейбница (достаточный признак
сходимости знакочередующихся рядов)
Если
для знакочередующегося ряда выполнены
2 условия:
1)
последовательность абсолютных величин
членов ряда монотонно убывает:
U1>U2>U3>…
2)
предел Un
при n→∞
= 0
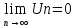 , то знакочередующийся ряд
сходится,
при этом сумма ряда не превосходит
первого члена ряда:
0 < S
< U1
, то знакочередующийся ряд
сходится,
при этом сумма ряда не превосходит
первого члена ряда:
0 < S
< U1
36.
Знакопеременным
называется ряд
содержащий
бесконечно много как положительных,
так и отрицательных членов.
Определение:
Рассмотрим ряд, если сходится ряд
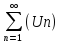 составленный из модулей членов исходящего
ряда, то исходящийряд
составленный из модулей членов исходящего
ряда, то исходящийряд
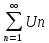 называетсяабсолютно
сходящимся.
Если
же ряд
называетсяабсолютно
сходящимся.
Если
же ряд
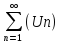 расходится, но при этом ряд
расходится, но при этом ряд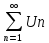 является сходящимся, то говорят, чтоисходный ряд
условно сходится.
является сходящимся, то говорят, чтоисходный ряд
условно сходится.
37. Ряд, членами которого является функция, зависящая от Х, называется функциональным рядом:
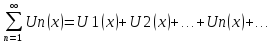 Среди
функциональных рядов особую роль играют
степенные
ряды, то есть
ряды вида:
Среди
функциональных рядов особую роль играют
степенные
ряды, то есть
ряды вида:
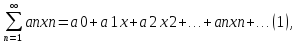 гдеa0,a1
и т.д. – числовые коэффициенты ряда. (
х – действительная переменная)
Теорема
Абеля: если
степень ряда (1) сходится при х=х*≠0, то
он абсолютно сходится при всех значениях
х удовлетворяющих неравенству
│х│<│x*│
Итак
область сходимости степени ряда
представляет собой интервал
вида (-│х*│, │х*│)
с возможно присоединяющимися к нему
концами.
Определение:
радиусом сходимости степенного ряда
(1) называют
неотрицательное число R,
такое, что при │х│< R
ряд сходится, а при │х│> R – расходится.
R
=
гдеa0,a1
и т.д. – числовые коэффициенты ряда. (
х – действительная переменная)
Теорема
Абеля: если
степень ряда (1) сходится при х=х*≠0, то
он абсолютно сходится при всех значениях
х удовлетворяющих неравенству
│х│<│x*│
Итак
область сходимости степени ряда
представляет собой интервал
вида (-│х*│, │х*│)
с возможно присоединяющимися к нему
концами.
Определение:
радиусом сходимости степенного ряда
(1) называют
неотрицательное число R,
такое, что при │х│< R
ряд сходится, а при │х│> R – расходится.
R
=
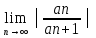
42. Пусть выполнены следующие предположения:
1. Число элементарных исходов конечно.
2. Все элементарные исходы равновозможны, тогда верны следующие классические ….
Под вероятностью Р(А) событие А понимается отношение числа элементарных исходов благоприятствующие событию А общему числу всех равновозможных элементарных исходов данного испытания. Р(А)=m/n. – n – общее число элементарных исходов; m – число элементарных исходов данного события А.
Обобщение классическим вероятности на бесконечное число элементарных исходов является геометрическая вероятность. Пусть равновозможные элементарные исходы являются точками органического множества G n-мерного пространства (n=1,2,3).
41. Элементарными событиями (или элементарными исходами) называется единственные возможные взаимно-исключающие исходы опыта, (неразложимые исходы опыта) обозначающие w1, w2 и т. д. А все общее исходов относится к данному опыту обозначается Ω={w1,w2,w3…} – и называется пространством элементарных исходов.
Алгебра
событий: 1)
Суммой двух
событий А и В
называется событие А+В (АᶸВ), состоящее
из всех элементарных принадлежащих по
крайней мере одному из событий А или В.
Событие А+В имеет место когда происходит
хотя бы одно из событий А или В. А+В. 2)
Произведение событий А или В
называется событие АВ (А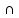 В)
состоящий из элементарных событий
принадлежащих А и В одновременно. Событие
А и В происходит когда происходит как
событие А, так и событие В одновременно.
АВ.
В)
состоящий из элементарных событий
принадлежащих А и В одновременно. Событие
А и В происходит когда происходит как
событие А, так и событие В одновременно.
АВ.
47. Универсальным способом задания случайной величины Х является ее функции распределения F(x) которая определяется следующим образом: F(x)=P(X˂x) – вероятность того, что СВ Х примет значение меньше х.
Свойства функции распределения:
1) 0≤F(x)≤1
2)
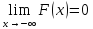 ,
,
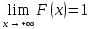
3) F(x) – неубывающая на всей числовой оси т. е. если х1˂х2 =˃ F(x1) ≤ F(x2)
4) P(x1≤ x ˂ x2)= F(x2) – F(x1)
5) F(x) непрерывна слева
6) P(X ≥ x) = 1 - P(X ˂ x) = 1 – F(x)
48. СВ Х называется дискретной или она принимает конечное или четное число значений.
Числовые характеристики ДСВ.
Математическим ожиданием ДСВ называют сумму произведений, значений, СВ на соответствующую им вероятности.
M(x)
=
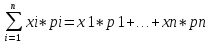
Дисперсией ДСВ называют математическое ожидание квадрата отклонения СВ от своего математического ожидания: Д(Х)=М(Х – М(Х))2
Для ДСВ формула дисперсий приобретает вид
Д(Х)
=
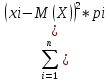
Средним квадратическим отклонением СВ называют квадратический корень из дисперсии
σ(Х)=