
- •4. Определенный интеграл с переменным верхним пределом:
- •6. Интегрирование по частям:
- •7. Вычисление площади в декартовой системе координат:
- •12. Несобственные интегралы второго рода:
- •9. Вычисление объема тела вращения:
- •10. Работа переменной силы:
- •11. Несобственные интеграла с бесконечными пределами интегрирования:
- •21. Метод вариации произвольных постоянных:
- •33. Достаточные признаки сравнения:
- •39. Ряды Маклорена для некоторых функций:
- •40. Приложения степенных рядов:
- •53. Нормальное распределение
21. Метод вариации произвольных постоянных:
Пусть y=C1(x)y1+C2(x)y2-где С1(х),С2(х) некоторые функции подлежащие определению
Для нахождения С1(х),С2(х) потребуем чтобы учн было решением уравнения y’’+py’+qy=f(x) (*)
Найдем учн’= C1(х)’y1++C1(x)y1’+C2(x)’y2+C2(x)y2’ , пусть для упрощения C1’(x)y1+C2’(x)y2=0, тогда y’чн=C1(x)y1’+C2(x)y2’ , далее y’’чн=C1’(x)y1’+C1(x)y1’’+C2’(x)y2’+C2(x)y2’’ подставляем в уравнение (*).
Требуем
(…………..)=f(x),
и так, чтобы y=C1(x)y1+C2(x)y2
было решением уравнения, должны выполнятся
следующие требования:
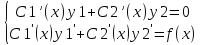
Из полученной системы определяем С1’(х), С2’(х), находим С1(х), С2(х): интегрированием
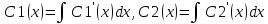
Записываем учн=С1(х)у1+С2(х)у2, после чего уон=уоо+учн
22. Метод неопределенных коэффициентов(метод подбора)
23.
Если существует предел интегральной
суммы
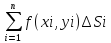 при n→∞(λ→0)
который не зависит ни от способа
разбиения области Д на части, ни от
выбора точек в них, то он называется
двойным
интегралом
от функции f(x,y)
по области Д и обозначается
при n→∞(λ→0)
который не зависит ни от способа
разбиения области Д на части, ни от
выбора точек в них, то он называется
двойным
интегралом
от функции f(x,y)
по области Д и обозначается
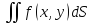 .
.
Свойства двойного интеграла:
Линейность:
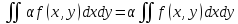
Аддитивность:
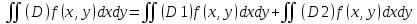
Монотонность: а). если f(x,y)≥0 в Д, то
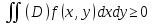 б). еслиf(x,y)≤g(x,y),
то
б). еслиf(x,y)≤g(x,y),
то
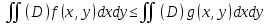
Оценка двойного интеграла: пусть м- наименьшее, М- наибольшее значения функции z=f(x,y) в области Д, тогда m(Sd)≤
 ≤M(Sd)
≤M(Sd)Аналог теоремы о среднем: пусть f(x,y) непрерывна в Д, тогда существует М0(х0,у0) ϵ Д что
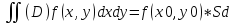
S(x)=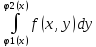 - площадь поперечного сечения
цилиндрического тела.
- площадь поперечного сечения
цилиндрического тела.
V=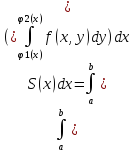 -
объем цилиндрического тела
-
объем цилиндрического тела
24.Если
существует предел интегральной суммы
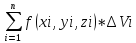 ,
при
,
при
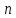 →∞(λ→0)
независящей ни от способа разбиения
области V
на части, ни от выбора точек в них, то он
называется тройным
интегралом
от функции f
по области V
и обозначается
→∞(λ→0)
независящей ни от способа разбиения
области V
на части, ни от выбора точек в них, то он
называется тройным
интегралом
от функции f
по области V
и обозначается
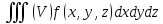
Свойства тройного интеграла:
Линейность

Аддитивность:
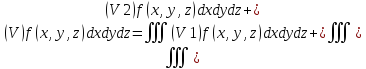
Монотонность: если f(x,y,z)≤g(x,y,z)
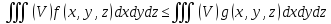
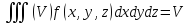 тела
тела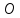 ценка
тройного интеграла: m*V≤
ценка
тройного интеграла: m*V≤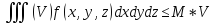
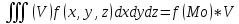
p=p(x,y,z)
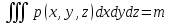 тела
тела
25.
Если существует предел интегральной
суммы
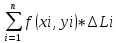 приn→∞(λ=max
приn→∞(λ=max
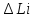 →0),
который не зависит ни от способа
разделения кривой на части, ни от выбора
точек
→0),
который не зависит ни от способа
разделения кривой на части, ни от выбора
точек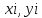 ,
то он называетсякриволинейным
интегралом
от функции f(x,y)
по длине дуги
,
то он называетсякриволинейным
интегралом
от функции f(x,y)
по длине дуги
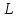 и обозначается:
и обозначается: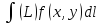
Свойства
КРИ-1: 1.
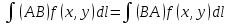
2.
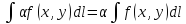
3.
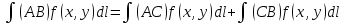
4.
f(x,y)≤g(x,y),

5.
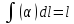 - длина дуги
- длина дуги
6.
p(x,y),
m=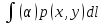
7.
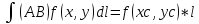 ,
где (хс,ус)
,
где (хс,ус)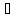 АВ
АВ
27. пусть функция Р(х,у), Q(х,у) непрерывны вместе со своими частными производными в области Д, тогда имеет место формула:
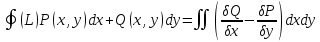
-где
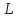 - граница области Д и интегрирование
- граница области Д и интегрирование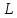 производится
в положительном направлении, когда
при движении по
производится
в положительном направлении, когда
при движении по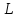 область Д остается слева. Называетсяформулой
ГРИНА, она
связывает КРИ-2 по границе области с
двойным интегралом, по самой области.
область Д остается слева. Называетсяформулой
ГРИНА, она
связывает КРИ-2 по границе области с
двойным интегралом, по самой области.
Условия независимости КРИ-2:
Для любой замкнутой кривой
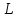 расположенной в Д:
расположенной в Д:
Для любых 2-х точек А и В лежащих в Д значений интеграла
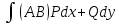 ,
не зависит от выбора пути интегрирования
целиком лежащего в Д.
,
не зависит от выбора пути интегрирования
целиком лежащего в Д.P(x,y)dx+Q(x,y)dy – представляет собой полный дифференциал некоторой функции u(x,y) определенного в области Д т.е. такой, что du=Pdx+Qdy
В области Д всюду :
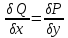
28.
Пусть задана поверхность S и функция
f(x,y,z),
разбивающая поверхность на части
площадями
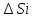 .
В каждой части произвольно выбирают
точку Мi(xi,yi,zi),
составляют интегральную сумму и находят
ее предел называемый поверхностным
интегралом(ПОВИ-1):
.
В каждой части произвольно выбирают
точку Мi(xi,yi,zi),
составляют интегральную сумму и находят
ее предел называемый поверхностным
интегралом(ПОВИ-1):
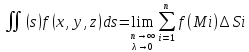
Свойства:
1. f=1
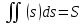 поверхности
поверхности
2.
Если задана плотность поверхности
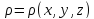 то,
то,
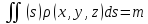 поверхности
поверхности
29.
Рассмотрим 3 непрерывные функции
P(x,y,z),
Q(x,y,z),
R(x,y,z)
и выберем определенную сторону поверхности
S (ориентированную поверхность). Выбранную
сторону S разбиваем на части, затем
проектируем эти части на координатные
плоскости и строим интегральные суммы
например:
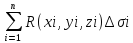 , где
, где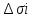 это площадь проекции соответствующей
части на плоскость Оху (+)-если нормаль
составляет с Оz
острый угол и (-) – если тупой. В пределе
при n→∞
такая сумма дает ПОВИ-2
это площадь проекции соответствующей
части на плоскость Оху (+)-если нормаль
составляет с Оz
острый угол и (-) – если тупой. В пределе
при n→∞
такая сумма дает ПОВИ-2
Общий вид ПОВИ-2:
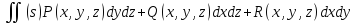
30. Если
в каждой точке М некоторой области задан
вектор
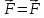 (M),
то
говорят, что в области
задано векторное
поле (если
рассматриваемая область на плоскости,
поле называется плоским).
(M),
то
говорят, что в области
задано векторное
поле (если
рассматриваемая область на плоскости,
поле называется плоским).
Характеристики
векторного поля:
1. Поток
ПS( векторного поля
векторного поля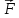 ,
через ориентированную поверхность
S называется ПОВИ-1 скалярного произведения
вектора
,
через ориентированную поверхность
S называется ПОВИ-1 скалярного произведения
вектора
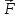 на единичный вектор нормали
на единичный вектор нормали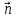 к поверхности
S: ПS(
к поверхности
S: ПS(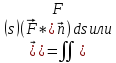
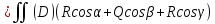
2.
Циркуляцией векторного поля вдоль
замкнутой ориентированной кривой L,
называется следующее КРИ-2: ЦL(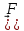 =
=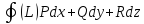
31. Дивергенцией
векторного поля
называется величина:
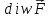 =
= он характеризует мощность источника,
если
он характеризует мощность источника,
если
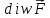 ˃0
в точке М и мощность стока, если
˃0
в точке М и мощность стока, если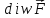 ˂0
в точке М.
˂0
в точке М.
Ротором
(вихрем) векторного поля
называется
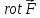 (m)=
(m)= = (
= (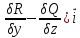 +
+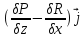 +
+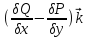
Если
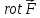 (m)
(m) поле
называется без
вихревым или потенциальным,
при этом существует такая скалярная
функция u(m)
что grad
u=
поле
называется без
вихревым или потенциальным,
при этом существует такая скалярная
функция u(m)
что grad
u=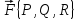 ,u-
называется потенциалом
поля.
,u-
называется потенциалом
поля.
Векторное поле в каждой точке которого дивергенция равна 0 , называется соленоидальным.
