Рис. 9.11

Заметим, что условие единственности главного лепестка ДН АР осевого излучения можно получить из (9.22), подставив ξ =1, тогда это условие примет вид d< λ /2. Изменение КНД и формы множителя направленности линейной антенны при варьировании коэффициента замедления ξ показано на рис. 9.11. Коэффициент А связан с D формулой D = 4A( L/λ ).

9.2.9. Системы излучателей с неравноамплитудным распределением

Равноамплитудные системы находят широкое применение на практике, так как обеспечивают самый узкий главный лепесток ДН. Однако эти системы, как показано выше, имеют сравнительно большой уровень боковых лепестков. Между тем, желательно уменьшить этот уровень, особенно в случаях, когда с направления боковых лепестков могут поступить интенсивные помехи. С этой целью применяют системы с неравноамплитудным распределением токов (полей). Если в системе излучателей изменять характер амплитудного распределения, то это будет приводить к изменению ширины главного лепестка и уровня боковых лепестков. Расчеты показывают, что чем сильнее спадает к краям системы амплитудное распределение, тем шире главный лепесток и меньше уровень боковых лепестков. Можно подобрать такое оптимальное амплитудное распределение, при котором уровень боковых лепестков является минимальным для заданной ширины главного лепестка или ширина главного лепестка оказывается минимальной для заданного уровня боковых лепестков.

Найдем оптимальное амплитудное распределение для эквидистантной синфазной АР. Пусть АР состоит из нечетного числа (2N+l) ненаправленных излучателей (рис.9.12). Предположим, что АР

синфазна. Полярный угол ϑ отсчитывается от нормали к АР.

d

Рис. 9.12

Тогда, подставляя в (9.5) ψn=0 и θn =π/2–ϑ, получаем множитель системы

N

fс(ϑ)= ∑aneiγρn sinϑ .

n=−N

Пусть амплитудное распределение симметрично an= –an. Кроме того, учтем, что n-й излучатель удален от середины АР на расстояние ρn=nd, тогда

N

fс(ϑ)=a0 +2 ∑an cosnu ,

n=−N

где u= γdsinϑ.

Обозначим cosu=x. Из тригонометрии известно, что косинус кратного угла (cosnu) может быть представлен в виде полинома степени n от cosu. Следовательно, множитель системы можно запи-

	N	B0,B1,...,BN
сать в виде	fс(ϑ)= ∑Bn xn . Коэффициенты		определяются через коэффициенты
	n=0
a0 ,a1 ,...,aN	путем решения системы (N+1) алгебраических уравнений.

Можно показать, что оптимальное амплитудное распределение соответствует такому выбору коэффициентов a0,a1,...,aN , следовательно, и коэффициентов B0,B1,...,BN , при котором множи-

85

тель системы выражается полиномом Чебышева Tn (αx) , где α – постоянная величина, опреде-

ляемая ниже. Таким образом,

N
fс(ϑ)= ∑Bn xn =T2N (ax) .	(9.28)

n=0

Напомним, что полиномы Чебышева записываются в виде

Tn(ξ)=cos(n arccosξ) при –1<ξ<1,	(9.29)
Tn(ξ)= ch(n archξ) при ξ<–1 и ξ>1.	(9.30)

Подставим значения n:

T0(ξ)=1; T1(ξ)=ξ; T2(ξ)=2ξ2–1; T3(ξ)=4ξ3–3ξ; T4(ξ)=8ξ4–8ξ2 +1.

T8 (ξ)

a=1.04

10

		α=1,04
			1
	ξξ
–ξ	--ξ		ξ		ξ
-	-1.0	-0.6	-0.2 0 0.2	0.6	1.0

Рис. 9.13

Для иллюстрации свойств полиномов Чебышева на рис.9.13 приведен график полинома T8(ξ). В интервале –1<ξ<1 наибольшие (по абсолютной величине) значения функции Tn(ξ) равны единице, за пределами этого интервала с ростом |ξ| функция монотонно возрастает, причем скорость нарас-

тания наибольшая из всех известных полиномов той же степени. Число максимумов в этом интервале равно (n–1).

Если выбрать α > 1, то монотонно возрастающая часть графика Tn (αx) будет соответствовать

главному лепестку ДН. Направление главного лепестка определяется значениями ϑ = 0; u = 0; x = 1; ξ = α (рис.9.13). Следовательно, величина главного максимума равна fc(0) = Tn(α)= ch(n archα).

Степень полинома Чебышева n на единицу меньше числа излучателей АР. Так как максимумы боковых лепестков равны единице, то их относительный уровень составляет

Fбок = 1/ch(n archα).

(9.31)

Первые нули ДН (ближайшие к главному лепестку) определяются наибольшим корнем уравнения Tn (αξ)=0 . Учитывая (9.29) получаем narccosαξ0 =π/2 , откуда ξ0=(1/α)×cos(π/2n). Так как

x=cos(γdsinϑ), то приравняв x=ξ0, получим

sinϑ = arccos[cos(π/2n)/α]/γd.

(9.32)

Можно показать, что 2ϑ0 >0 (ширина главного лепестка на нулевом уровне) для полинома Че-

бышева имеет наименьшую величину из всех полиномов той же степени.

Если задан уровень боковых лепестков, то из (9.31) можно найти параметр α, а из (9.32) – ширину главного лепестка по нулям.

Оптимальность рассчитанной таким образом ДН является следствием того, что из всех полиномов степени n полином Чебышева Tn (ξ) наименее уклоняется от нуля на отрезке –1 ≤ξ≤ 1.

Следовательно, ДН, описываемая полиномом, имеет наименьший уровень боковых лепестков. Для нахождения оптимального амплитудного распределения необходимо в (9.28) приравнять ко-

эффициенты при одинаковых степенях и таким образом определить коэффициенты BN . Затем,

86

используя указанную ранее связь между коэффициентами	a	,a ....	и	B ,B ,... , рассчитать ампли-
	0	1		0	1

тудное распределение.

Оптимальные распределения не всегда можно реализовать, поэтому часто ограничиваются квазиоптимальными. Кроме оптимальных и квазиоптимальных амплитудных распределений, в теории антенн известны различные виды спадающих к краям амплитудных распределений, позволяющих за счет некоторого расширения главного лепестка уменьшить уровень боковых лепестков. Следует отметить, что численные характеристики антенн со спадающим к краям амплитудным распределением сохраняются неизменными в режиме сканирования, если только луч не приближается к оси антенны ближе двух-трех значений его ширины по половинной мощности.

9.2.10.Неэквидистантные антенные решетки

Боковые лепестки при заданной ширине главного лепестка могут быть ослаблены не только оптимальным амплитудным распределением в эквидистантой АР, но и оптимальным расположением излучателей в неэквидистантной равноамплитудной АР. Эти две системы в некотором смысле эквивалентны друг другу.Пусть имеется эквидистантная АР с неравноамплитудным, близким к оп-

тимальному распределением амплитуды а( zn ), где zn – координата n-го излучателя, n=1, 2, ..N

(рис.9.14, а). Для простоты рассуждений положим, что N велико, а расстояния d между соседними излучателями малы. Тогда дискретную АР можно заменить непрерывной системой с линейной плотностью тока по системе (амплитудным распределением), равной

a'(z) = a(zn)/d .

(9.33)

а)

0	d	N	d

б)

б)

z'	z''	Z’	Z’’		z	z

	в)	в)
		az=const

1	2	3	Рис 92 12	z	z
			Рис. 9.14

Функция a'(z) ступенчатая, однако, полагая, что токи в соседних излучателях отличаются не резко и учитывая малость d, эта функция на рис. 9.14, б изображена плавной кривой. Площадь, ограниченная кривой a'(z) и осью абсцисс, определяет полный ток системы. Разобьем эту площадь на N1 площадок одинаковой величины А, тогда

A= 1 L∫a'(z)dz ,

N1 z=0

где L – длина системы излучателей. Рассмотрим одну площадку, соответствующую отрезку ∆z =z" −z' (рис.9.14, б). Для нее

z=z"

A= ∫a'(z)dz .

z=z'

Заменим теперь непрерывную систему решеткой N1 дискретных излучателей, абсциссы которых равны абсциссам центров тяжести указанных выше площадок, а амплитуды равны величине А

87

(рис.9.14, в). Так как линейные плотности токов этих двух систем равны, то A/∆z =a'(z) или

∆z =A/a'(z) . Подставим значение a'(z) из (9.33): ∆z=Ad/a(zn). Расстояния между соседними излуча-

телями неэквидистантной АР при больших N1 практически равны ∆z , следовательно, они обратно пропорциональны величинам токов в соответствующих излучателях эквидистантной АР.

Практическая реализация неэквидистантной АР проще, чем реализация эквидистантной неравноамплитудной решетки. Другим достоинством неэквидистантной АР является то, что разности хода лучей от соседних излучателей различны для любого направления, кроме нормального к оси АР. Поэтому у неэквидистантной АР подавлены побочные главные максимумы. При заданной ширине ДН число излучателей неэквидистантной АР может быть меньше, чем у эквидистантной, поскольку ширина ДН зависит в основном от длины АР и в меньшей степени от закона расположения ее излучателей.

9.2.11. Влияние фазовых искажений на параметры линейной антенны

Синфазное либо линейное фазовое распределение возбуждения в линейной антенне приводит к синфазному сложению излучений отдельных элементов в направлении главного максимума. На практике из-за несовершенства конструкции распределителя, а также из-за ошибок изготовления отдельных элементов антенной системы линейность фазового возбуждения часто оказывается нарушенной, что ведет к искажению формы ДН и снижению КНД. При этом ситуация оказывается различной в случаях детерминированных (систематических) и случайных фазовых искажений.

Распределение детерминированных фазовых ошибок по длине антенны обычно является достаточно гладким, в связи с чем принято представлять его в форме степенного ряда

a(z)= a(z) expi[ψ(z)–ηγz];

ψ(z) = ψ1(2z/L) + ψ2(2z/L)2 + ψ3(2z/L)3 + ...,

(9.34)

где a(z) – амплитудное распределение; exp(–iηγz) – задаваемое заранее фазовое распределение, обеспечивающее сканирование; ψ(z) – распределение фазовой ошибки возбуждения. Величины ψj, j=1, 2, ..., представляют собой максимальные значения фазовой ошибки степени j на краю антенны, т. е. при z = L/2. Выясним характерные искажения формы ДН, возникающие из-за отдельных слагаемых в ряде (9.34) для функции ψ(z).

Наличие линейных фазовых искажений не нарушает общего линейного закона распределения фазы возбуждения, а лишь изменяет величину коэффициента замедления, который становится

равным ηэкв = η–2ψ/(γL). Это приводит лишь к сдвигу характеристики направленности на некоторый угол в сторону конца антенны, получившего дополнительное запаздывание.

Квадратичные фазовые искажения, как показывают вычисления, проведенные по формуле (9.5), не вызывают смещения максимума множителя направленности, однако приводят к расширению главного лепестка и «заплыванию» минимумов излучения. Наиболее сильно квадратичные фазовые искажения сказываются при равномерном амплитудном распределении. Здесь для случая

ψ2 >π наблюдается даже раздвоение главного лепестка. При спадающем амплитудном распреде-

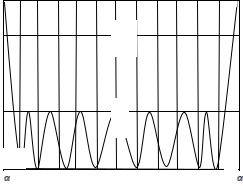
лении наиболее сильно расфазированные края антенны дают меньший вклад в общее излучаемое поле и искажения диаграммы направленности меньше. Для сравнения на (рис.9.15, а) изображен множитель линейной равноамплитудной решетки излучателей при отсутствии квадратичных фазовых ошибок, на (рис.9.15, б) при равноамплитудном и на (рис.9.15, в) при косинусоидальном

амплитудном распределении и наличии максимальной квадратичной ошибки ψ=π/2.

a)

б)

в)

F(

F(

F(

-8 -4 0 4 8 u	-8 -4 0 4 8 u		-8 -4 0 4 8 u

Рис. 9.15

88