Предел функции

Допустим, значения аргумента можно выбирать как угодно близко к, то говорят, что «стремится к», и обозначают . (Возможно, !)

Если значение функции можно выбрать как угодно близким к величинеза счет того, что, то говорят, что «значение функциистремится кпри» или «– пределпри» и обозначают . При этом для всех , близких к.

!!! (предел функции равен ее значению)непрерывна в точке .

Функция –бесконечно малая б/м (большая б/б) при , если (.

Свойства пределов функций

1. Если предел функции в точке существует, то только один.

2. Арифметические операции над пределами. Если ,– конечные пределы, то

, ,(при).

! При нарушении условия говорят о неопределенностях: , , , .

3. Если () и– вещественное число, отличное от нуля, то .

4. Если (), то вблизи точки:, где.

5. Предел сложной функции. Пусть 1) функции иопределены на множествахисоответственно; 2),,; 3), 4) для всех; 5)(). Тогда.

Свойства бесконечно малых и бесконечно больших функций

1. Если – б/м при, то– б/б при, и наоборот.

2. Произведение б/м величины на ограниченную величину (не являющуюся бесконечно большой) есть б/м.

3. Произведение б/б на величину, не являющуюся б/м, есть б/б.

4. Сумма любого конечного числа б/б (бесконечно больших одного знака) есть б/м (б/б того же знака).

5. Произведение б/м есть б/м.

Пример 1. .

Пример 2. .

Замечательные пределы

Первый замечательный предел: .

Следствия: 1) ,,, ;

2) ,,,приблизких к нулю.

Второй замечательный предел: .

Следствия: 1) ,,;

2) ,,при , близких к нулю.

Некоторые значения пределов функций:

1) 2), 3), 4)

5) (показательная функция растет быстрее, чем степенная функция),

6) (степенная функция растет быстрее, чем логарифмическая),

7)

Пример 3. .

Пример 4.

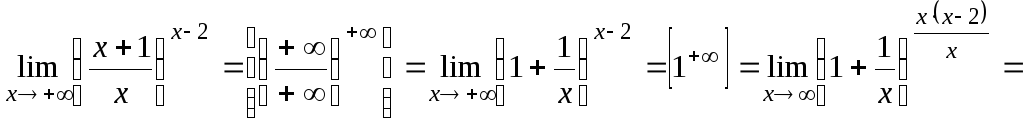
Асимптоты

Определение. Точка –вертикальная асимптота функции еслиили,. При этом прямая– вертикальная асимптота графика функции

Определение. Линейная функция –наклонная асимптота функции приеслиПрямая– наклонная (горизонтальная при) асимптота графика функции.

Критерий существования наклонных асимптот. Функция имеет принаклонную асимптотутогда и только тогда, когда существуют конечныеи

ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ

№	Обозначение	Область определения	Область значений	Монотонность	Свойства	График
1	2	3	4	5	6	7
Степенная функция
1.			, если – нечётно	возрастает на , если– нечётно	нечётная, если – нечётно, непериодическая
			, если – чётно	убывает на , возрастает на, если– чётно	чётная, если – чётно, непериодическая
2.			если – нечётно	убывает на и на, если– нечётно	нечётная, если – нечётно, непериодическая
			, если – чётно	возрастает на и убывает на, если– чётно	чётная, если – чётно, непериодическая
3.		, если – нечётно	, если – нечётно	возрастает на , если– нечётно	нечётная, если – нечётно, непериодическая
		, если – чётно	, если – чётно	возрастает на , если– чётно	ни чётная, ни нечётная, если – чётно, непериодическая
Показательная функция
4	,			возрастает на , если	не является ни чётной, ни нечётной, непериодическая
				убывает на , если

1	2	3	4	5	6	7
Логарифмическая функция
5.	,			возрастает на , если	не является ни чётной, ни нечётной, непериодическая
				убывает на , если
Тригонометрические функции
6.				возрастает на , убывает на,	нечётная, периодическая с периодом
7.				возрастает на , убывает на,	чётная, периодическая с периодом
8.				возрастает на	нечётная, периодическая с периодом
9.				убывает на	периодическая с периодом , нечетная
Обратные тригонометрические функции
10.				возрастает на	нечётная, непериодическая
11.				убывает на	не является ни чётной, ни нечётной, непериодическая
12.				возрастает на	нечётная, непериодическая
13.				убывает на	не является ни чётной, ни нечётной, непериодическая