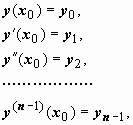1. Дифференциальными уравнениями называются такие уравнения, в которых неизвестными являются функции одного или нескольких переменных, причем в уравнения входят явно производные искомых функций до некоторого порядка. 

Дифференциальное уравнение первого порядка в общем случае содержит:  1) независимую переменную ; 2) зависимую переменную  (функцию); 3) первую производную функции: .

Общий вид такого уравнения следующий:

Решением уравнения (1.1) называется такая функция x =(t) независимого переменного t, определения на некотором интервале r₁  <  t  <  r₂ (случаи r₁ =  и r₂ = + не исключаются), которая дифференцируема в каждой точке этого интервала и при подстановке ее вместо x в соотношение (1.1) мы получаем тождество (по t) на всем интервале r₁ < t < r₂.

Интервал r₁ < t < r₂ называется интервалом определения решения (t).

Пример общего решения:

->

Ответ: общее решение: . 

Задача об отыскании решения y=y(x) дифференциального уравнения y'=f(x, y), удовлетворяющего начальному условию y(x0)=y0, называется задачей Коши. Решение задачи Коши называют частным решением. по условию требуется найти частное решение ДУ, удовлетворяющее заданному начальному условию. Такая постановка вопроса также называется задачей Коши.

Найти частное решение дифференциального уравнения , удовлетворяющее начальному условию 

Переписываем производную в нужном виде:

Очевидно, что переменные можно разделить, мальчики – налево, девочки – направо:

Интегрируем уравнение:

Итак, общее решение: 

В чём состоит задача? Необходимо подобрать такое значение константы , чтобы выполнялось условие .

Оформить можно по-разному, но понятнее всего, пожалуй, будет так. В общее решение вместо «икса» подставляем ноль, а вместо «игрека» двойку: То есть, 

Стандартная версия оформления:

Теперь в общее решение  подставляем найденное значение константы :  – это и есть нужное нам частное решение.

Ответ: частное решение: 

Интегральной кривой называется график решения геометрически неопределённого интеграла (первообразной), представляющего собой семейство «параллельных» кривых , где каждому числу С соответствует определенная кривая семейства. График каждой кривой и называется интегральной кривой. График решения дифференциального уравнения называют интегральной кривой.

Для дифференциального уравнения y'=f(x, y), правая часть которого f(x, y) и ее частная производная по y непрерывны в некоторой области D имеет место геометрическая интерпретация, называемая полем направлений.

Если через каждую точку (x, y) области D провести некоторый отрезок l(x, y) с угловым коэффициентом, равным значению правой части f(x, y) в точке (x, y), то получится изображение, которое называется "полем направлений". Любая интегральная кривая y=y(x) в каждой своей точке (x, y(x)) касается отрезка l(x, y).

Частному решению соответствует одна интегральная кривая, проходящая через некоторую заданную точку. Частное решение изобразится параболой (рис. 1. ) проходящей через точкуЗаметим, что задать начальное условие для уравнения первого порядка с геометрической точки зрения означает задать точку , через которую должна пройти соответствующая интегральная кривая.

Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения. То есть,  – это общий интеграл.

Опр. Общим решением (общим интегралом) уравнения (1) называется такое соотношение

;

(2)

что: 1. Любое решение (2)  относительно y (для набора постоянных C₁, C₂, …, C_n из некоторой области n-мерного пространства) - частное решение уравнения (1);  2. Любое частное решение уравнения (1) может быть получено из (2) при некотором наборе постоянных C₁, C₂, …, C_n. 

Опр. Частным решением уравнения на интервале (a, b) (конечном или бесконечном) называется любая n раз дифференцируемая функция , удовлетворяющая этому уравнению, т.е. обращающая уравнение на этом интервале в тождество. Опр. Общим решением (общим интегралом) уравнения называется такое соотношение , что: 1. Любое решение этого соотношения относительно y (для набора постоянных C₁, C₂, …, C_n из некоторой области n-мерного пространства) является частным решением уравнения ; 2. Любое частное решение уравнения может быть получено из общего решения при некотором наборе постоянных C₁, C₂, …, C_n. Мы будем в основном рассматривать дифференциальные уравнения в форме, разрешённой относительно старшей производной:

;

(3)

и получать общее решение в форме

;

(4)

решённой относительно неизвестной функции.

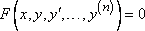2. Уравнение  называется дифференциальным уравнением -го порядка.

Дифференциальным уравнением n-го порядка называется уравнение вид  y ⁽ⁿ⁾ = f (x, y, y ', …, y ^{(n – 1)}).       (1)

или

   y ⁽ⁿ⁾ + p₁ (x) y ^{(n – 1)} + … + p_{n – 1} (x) y ' + p_n (x) y = f (x).                                                         (2)

Теорема 1 (существования и единственности решения)

Если в уравнении y⁽ⁿ⁾ = f(x, y, y, ..., y^(n1)) функция f(x, y, y, ..., y^(n1)) и её частные производные по аргументам y, y, ..., y^(n1) непрерывны в некоторой области, содержащей значения x = x₀, y = y₀, y =  ...,  то существует единственное решение этого уравнения y = (x),  удовлетворяющее условиям  /////////                                                       (3)

Условия (3) называются  начальными  условиями.  Задачей Коши для дифференциального уравнения (2) называется задача отыскания решения у(х), удовлетворяющего заданным начальным условиям/////// 

где х₀, у₀, , …, у₀^(n1)  – заданные числа.

Геометрически задача Коши формулируется следующим образом: среди всех интегральных кривых данного дифференциального уравнения выделить ту, которая проходит через заданную точку М₀(х₀, у₀) и для которой при х = х₀ имеют место равенства

Решение задачи Коши называют частным решением уравнения (2).

Определение 1

Общим решением дифференциального уравнения n-го порядка называется функция , где С_i – произвольные постоянные такие, что:

а) она удовлетворяет уравнению при любых значениях постоянных;

б) при заданных начальных условиях (3) постоянные можно подобрать так, что функция  будет удовлетворять этим условиям.

Соотношение Ф(х, у, C₁, C₂, …, C_n) = 0 называется общим  интегралом дифференциального  уравнения.  Оно неявно определяет общее решение уравнения (1).

Обыкновенным дифференциальным уравнением n –го порядка называется уравнение вида

F (x, y(x), y '(x), y ''(x),  …  , y⁽ⁿ⁾(x)) = 0,

где F — известная функция (n + 2)-х переменных, x — независимая переменная из интервала (a,b), y(x) — неизвестная функция. Число nназывается порядком уравнения.

Функция y(x) называется решением (или интегралом) дифференциального уравнения на промежутке (a, b), если она n раз дифференцируема на (a, b) и при подстановке в уравнение обращает его в тождество.

Обыкновенные дифференциальные уравнения, разрешенные относительно старшей производной, называют уравнениями в нормальной форме:

y⁽ⁿ⁾ = f(x, y, y ',  y '',  …  , y^{(n − 1)}).

Дифференциальное уравнение обычно имеет бесконечно много решений. Чтобы выделить нужное решение, используют дополнительные условия.

Чтобы выделить единственное решение уравнения n–го порядка обычно задают n начальных условий y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1}.

Задачей Коши (или начальной задачей) называется задача отыскания решения y = y(x) уравнения

F(x, y(x), y '(x), y ''(x),  …  , y^(n )(x)) = 0,    x>x₀,

удовлетворяющего условиям

y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1}.

Условия   y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1} называются начальными данными, начальными условиями или данными Коши.

 

Любое конкретное решение y = φ(x) уравнения n –го порядка F(x, y(x), y '(x), y ''(x),  …  , y^(n )(x)) = 0, называется частным решением.

Общим решением дифференциального уравнения

F(x, y(x), y '(x), y ''(x),  …  , y^(n )(x)) = 0

называется функция

y = Ф(x,  С₁, С₂, … , С_n),

содержащая некоторые постоянные (параметры) С₁, С₂, … , С_n, и обладающая следующими свойствами:

1. Ф(x, С₁, С₂,  … , С_n) является решением уравнения при любых допустимых значениях С₁, С₂, … , С_m;

2. для любых начальных данных  y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1}, для которых задача Коши имеет единственное решение,

существуют значения постоянных С₁ = A₁, С₂ = A₂,  … , С_n = A_n, такие что решение y = Ф(x, A₁, A₂,  …, A_n) удовлетворяет заданным начальным условиям.

Иногда частное или общее решение уравнения удается найти только в неявной форме: f(x, y) = 0 или G(x, y, С₁,  С₂,  ..., С_n) = 0.

Такие неявно заданные решения называются частным интегралом или общим интегралом уравнения.

Если задачу об отыскании всех решений дифференциального уравнения удается свести к алгебраическим операциям и к вычислению конечного числа интегралов и производных от известных функций, то уравнение называется интегрируемым в квадратурах. Класс таких уравнений относительно узок.

Для решения уравнений, которые не интегрируются в квадратурах, применяются приближенные или численные методы.

Задача теории обыкновенных дифференциальных уравнений — исследование общих свойств решений, развитие точных, асимптотических и численных методов интегрирования уравнений.

Дифференциальные уравнения первого порядка
I. Уравнения с разделяющимися переменными	II. Уравнения, однородные относительно переменных	III. Уравнения в полных дифференциалах	IV. Линейные дифференциальные уравнения
y' = f (x) g ( y)	y' = f (x, y), где f (x, y) — однородная функция нулевого порядка	M(x, y) dx + N(x, y) dy = 0, где	y' + P(x) y = Q(x)
y' = . Разделить переменные. Проинтегрировать.	Замена  = u, где u = u(x). После подстановки получим уравнение с разделяющимися переменными. Решив его, заменим u = .	Проверяем . Решением дифференциального уравнения является u(x,y), где  = M(x, y),  = N(x, y).	y' + P(x) y = 0 — линейное однородное дифференциальное уравнение с разделяющимися переменными. y' + P(x) y = Q(x) метод вариации произвольной постоянной; метод Бернулли:  y = u(x) · v(x).

Дифференциальное уравнение вида  y' = f (x) g ( y)  или  M(x) N( y) dx + P(x) Q ( y) dy = 0  называется уравнением с разделяющимися переменными.

   Можно сделать преобразование так, чтобы в одной части была одна переменная, в другой — другая.

             dx +  dy = 0,

где  dx — дифференциал некоторой функции от x,

 dy — дифференциал некоторой функции от y.

   Общий интеграл, выраженный в квадратурах:

              dx +   dy = C.

   Частный интеграл, удовлетворяющий условию  = y₀, выражается

              dx +   dy = 0.

   Если работать с уравнением y' = f (x) g ( y), то  = f (x) dx — уравнение с разделенными переменными.

Функция f (x, y) называется однородной функцией степени n относительно переменных x и y, если при любом допустимом t справедливо тождество f(tx, ty) ≡ tⁿ f (x, y).

   Дифференциальное уравнение первого порядка называется однородным относительно переменных x и y, если функция f (x, y) есть однородная функция нулевой степени относительно переменных x и y. Как определить, что дифференциальное уравнение приводится к однородному

Для того, чтобы определить, что дифференциальное уравнение приводится к однородному, нужно выделить две линейные формы: a₁ x + b₁ y + c₁, a₂ x + b₂ y + c₂,  и выполнить замену:  a₁ x + b₁ y + c₁ → t(a₁ x + b₁ y + c₁); a₂ x + b₂ y + c₂ → t(a₂ x + b₂ y + c₂)  Если после преобразований t сократится, то это уравнение приводится к однородному.

   Пусть имеем дифференциальное уравнение y' = f (x, y), однородное относительно переменных x и y. Положив t =  в тождестве f (tx, ty) = f (x, y), получим f (x, y) = f 1,  , т.е. однородная функция нулевого измерения зависит только от отношения аргументов.

   Обозначив f 1,  = φ, получим, что однородное относительно переменных x и y дифференциальное уравнение всегда можно представить в виде

             = φ.

   Как интегрируется уравнение y' = φ?

   Оно сводится к уравнению с разделяющимися переменными. Для этого делают замену

             = u,

где u — новая искомая функция от независимой переменной x, т.е. u = u(x).

   Тогда

            y = ux.

   Дифференцируя по x, имеем:

            y' = u' x + u,

тогда данное уравнение примет вид:

             u' x + u = φ(u)

или

            x = φ(u) – u.

   Это есть дифференциальное уравнение с разделяющимися переменными, преобразовав которое, получим:

             = .

   Интегрируя, получим:

             =  + C,

тогда

             = ln x + ln C

или

             = ln Cx,

причем |x| не пишем, т.к. –1 войдет в постоянную C.

   После взятия квадратуры, подставляем u = .

Дифференциальное уравнение вида M(x, y) dx + N(x, y) dy = 0 называется уравнением в полных дифференциалах, если .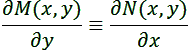

   Если существует функция u(x, y) такая, что

            M(x, y) = , N(x, y) = ,

то дифференциальное уравнение

             M(x, y) dx + N(x, y) dy = 0      (5.2)

можно переписать в форме

             dx +  dy = 0, т.е. d[u(x, y)] = 0.

В этом случае, данное уравнение имеет решение

            u(x, y) = C.

   Другой вопрос, как найти эту функцию u(x, y)?

   Это можно сделать с помощью криволинейного интеграла, но на практике поступают следующим образом.

   Т.к.  = M(x, y), то

             u(x, y) = M(x, y) dx + C(y),      (5.3)

где C(y) — функция, зависящая только от y и пока нам неизвестная. Будем ее искать из условия, что  = N(x, y), но

             = M(x, y) dx + C(y).

   Значит,

            M(x, y) dx + C'(y) = N(x, y).

   Отсюда находим C'(y), а интегрированием найдем C(y), которое затем подставляем в (5.3) и получаем u(x, y). Тогда общий интеграл уравнения (5.2)имеет вид

            u(x, y) = C. 

Уравнение вида y' + P(x) y = Q(x), левая часть которого есть линейная функция относительно y и y' , а функции P(x) и Q(x) непрерывны в некоторой области, называется линейным дифференциальным уравнением первого порядка.

   Уравнение вида y' + P(x) y = 0 называется линейным однородным дифференциальным уравнением первого порядка.

   Рассмотрим линейное однородное дифференциальное уравнение y' + P(x) y = 0. Это и уравнение с разделяющимися переменными, значит,

             = – P(x) y

или

             = – P(x) dx.

Проинтегрируем последнее уравнение:

             = – P(x) dx + C,

            ln y = ln C – P(x) dx.

Общее решение линейного однородного дифференциального уравнения имеет вид

            y = C.

 Рассмотрим одно нелинейное уравнение, которое всегда приводится к линейному. Это уравнение Бернулли:

            y' + p(x)y = q(x)y^m  (m ≠ 0, m ≠ 1).

   Для приведения уравнения Бернулли к линейному уравнению избавимся сначала в правой части от множителя y^m, разделив на него обе части уравнения. Получим

            y^{– m}y' + p(x)y^{1 – m} = q(x).

   Это уравнение можно переписать в виде

            ( y^{1 – m} )^' + p(x)y^{1 – m} = q(x).

   Введя новую неизвестную функцию z:

            z = y^{1 – m},

придем к уравнению

            z' + p(x)z = q(x),

или

            z' + (1 – m)p(x)z = (1 – m)q(x).

   Это есть линейное уравнение. Найдя его общее решение, получим общее решение уравнения Бернулли по формуле

            y = .

   Заметим, что если m > 0, то уравнение Бернулли имеет решение y ≡ 0. Это решение будет особым, если 0 < m < 1. 

Задачей Коши (или начальной задачей) называется задача отыскания решения y = y(x) уравнения

F(x, y(x), y '(x), y ''(x),  …  , y^(n )(x)) = 0,    x>x₀,

удовлетворяющего условиям

y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1}.

 

Условия   y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1} называются начальными данными, начальными условиями или данными Коши.

Любое конкретное решение y = φ(x) уравнения n –го порядка F(x, y(x), y '(x), y ''(x),  …  , y^(n )(x)) = 0, называется частным решением.

Общим решением дифференциального уравнения

F(x, y(x), y '(x), y ''(x),  …  , y^(n )(x)) = 0

называется функция

y = Ф(x,  С₁, С₂, … , С_n),

содержащая некоторые постоянные (параметры) С₁, С₂, … , С_n, и обладающая следующими свойствами:

1. Ф(x, С₁, С₂,  … , С_n) является решением уравнения при любых допустимых значениях С₁, С₂, … , С_m;

2. для любых начальных данных  y(x₀) = y₀,  y '(x₀) = y₁,  y ''(x₀) = y₂,  …  , y^{(n − 1)}(x₀) = y_{n − 1}, для которых задача Коши имеет единственное решение,

существуют значения постоянных С₁ = A₁, С₂ = A₂,  … , С_n = A_n, такие что решение y = Ф(x, A₁, A₂,  …, A_n) удовлетворяет заданным начальным условиям.

Иногда частное или общее решение уравнения удается найти только в неявной форме: f(x, y) = 0 или G(x, y, С₁,  С₂,  ..., С_n) = 0.

Такие неявно заданные решения называются частным интегралом или общим интегралом уравнения.

Дифференциальные уравнения, допускающие понижение порядка
Уравнение вида y^(^n^) = f (x).	Уравнение вида F (x, y, y ', …, y^(^n^)) = 0, не содержащее явно неизвестную функцию y.	Уравнение вида F (x, y^(^k^), y^(^k^+ 1), …, y^(^n^)) = 0, не содержащее явно неизвестную функцию, а также несколько ее первых производных.	Уравнение вида F (x, y, y ', …, y^(^n^)) = 0, не содержащее явно независимую переменную x.
Решение дифференциального уравнения сводится к последовательному применению квадратур. Общее решение содержит n произвольных постоянных.	Сделав замену y ' = z, где z = z(x), сводим данное уравнение к уравнению более низкого порядка. Решив его, заменяем z = y ' и находим y.	Производим замену y^(^k^) = z, где z = z(x). Решив полученное уравнение, заменяем z = y^(^k^) и интегрированием находим y.	Сделав замену y ' = z, где z = z(y), получим дифференциальное уравнение (n – 1)-го порядка, связывающее y, z и производные от z по y. Например, в дифференциальном уравнении вида F ( y, y ', y '' ) делается замена y ' = z, тогда y '' = = = z. Заменяя y ' = z, y '' = z, получим дифференциальное уравнение первого порядка F y, z, y ', z = 0.

1. Уравнения, не содержащие искомой функции и нескольких последовательных производных.

Пример 1.  Решить уравнение .

Решение.

В это уравнение явно не входит неизвестная функция. Следовательно, полагая , получим дифференциальное уравнение первого порядка

.

Разделяя переменные и интегрируя, имеем

,

Переходя к старым переменным, получим дифференциальное уравнение

,

интегрируя которое, получим

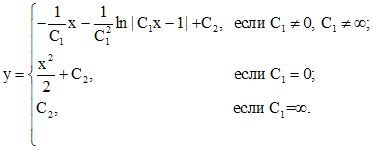
2. Уравнения, не содержащие явно независимой переменной.

Пример 2.  Решить уравнение .

Решение.

Уравнение не содержит явно переменную x,  делая замену  , уравнение запишется в виде

.

Отсюда находим . Из первого из двух последних уравнений получаем y=C, а из второго имеем , или , откуда

.

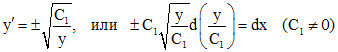Интегрируя, находим

.

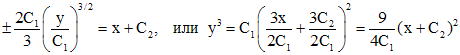Окончательно имеем

,

где   - новая произвольная постоянная.

3. Уравнения, однородные относительно .

Пример 3.  Решить уравнение  .

Решение.

Поскольку функция вследствие тождества

однородная относительно переменных , то данное дифференциальное уравнение однородное с показателем однородности 2. Следовательно, применив подстановку , получим уравнение

.

Это уравнение Риккати. Непосредственной проверкой можно убедится, что есть частное решение. Поэтому посредством подстановки приходим к линейному уравнению

,

решая которое, получаем окончательный ответ

.

4. Обобщенно - однородные уравнения.

Пример 4.  Решить уравнение .

Решение.

Проверим, что уравнение является однородным. С этой целью вместо переменных подставим в выражение для функции соответственно и, если это возможно, подберем значение k таким образом, чтобы выполнялось тождество

.

Очевидно, что такое тождество выполняется лишь при условии 4k=2, т.е при k=1/2 (при этом m=2). Следовательно, данное уравнение обобщенно однородное. Применив подстановку , получим уравнение

.

Последнее уравнение явно не содержит переменную t, поэтому посредством замены понижаем порядок на единицу:

.

Проинтегрировав последнее уравнение, находим

.

Далее, интегрируем уравнение

:

и получаем окончательно решения уравнение в виде

.

5. Уравнение в точных производных.

Пример 5.  Решить уравнение .

Решение.

Имеем

 ,

откуда следует, что

,

или

.

Это линейное уравнение первого порядка, и его общее решение имеет вид

.

5. Опр. Линейным дифференциальным уравнением n-го порядка называется уравнение, в которое неизвестная функция y(x) и её производные входят линейно, т.е. в первой степени:

Если правая часть уравнения тождественно равна нулю на рассматриваемом интервале (f(x)=0 при ), то уравнение называется однородным. Таким образом, однородное уравнение - это уравнение вида

;

(21)

Задача Коши для уравнений (20) и (21) ставится также, как и для общего уравнения n-го порядка (17) : требуется найти решение уравнения (20) или (21), удовлетворяющее начальным условиям

(22)

где y₀, y₁, y₂, …, y_n-1 - заданные числа. Для уравнения (17) теорема существования и единственности решения задачи Коши требовала непрерывности функции и её производных ; если привести (20) к виду (17): , то . Таким образом, условия теоремы Коши приводят к необходимости непрерывности функций f(x) и p_i(x), i = 1, 2, …, n. Далее, вывод теоремы Коши для уравнения (17) заключался в том, что найдётся окрестность точки x₀, в которой существует однозначно определённое решение задачи Коши; для линейных уравнений (20) и (21) вывод более глобален: единственное решение существует на всём интервале (a, b), на котором выполняются условия теоремы: Теорема существования и единственности решения задачи Коши для линейного уравнения: если функции f(x), p_i(x), i = 1, 2, …, n непрерывны на интервале (a, b), x₀ - произвольная точка этого интервала, то для любых начальных условий (22) существует единственная функция y(x), определённая на всём интервале (a, b) и удовлетворяющая уравнению (20) и начальным условиям (22). Всё дальнейшее изложение ведётся в предположении, что условия теоремы существования и единственности решения задачи Коши выполняются, даже если это не оговаривается специально.

6. линейного неоднородного дифференциального уравнения n-го порядка

 a₀(x)y⁽ⁿ⁾+a₁(x)y^(n-1)+…+a_n-1(x)y^/+a_n(x)y=f(x),   (1)

где a₀(x),…,a_n(x),f(x) – непрерывны на некотором интервале l

Принцип суперпозиции. Если и – решения однородного уравнения то

y (x) = α₁ y₁ (x) + α₂ y₂ (x)

при любых постоянных α₁ и α₂ является решением однородного уравнения.

Если и – решения неоднородного уравнения то их разность

y (x) = y₁ (x) – y₂ (x)

есть решение однородного уравнения

Всякое решение неоднородного уравнения есть сумма частного решения этого неоднородного уравнения и общего решения соответствующего ему однородного уравнения

Последние равенства означают:

разность любых двух решений линейного неоднородного уравнения (3) является решением соответствующего однородного уравнения (4);

сумма решения линейного неоднородного уравнения (3) и решения соответствующего однородного уравнения (4) является решением неоднородного уравнения.

7. Дифференциальное уравнение вида     (1)где 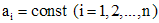, f - известная функция, называется линейным дифференциальным уравнением n - го порядка с постоянными коэффициентами.

Если f - непрерывная функция, то общее решение уравнения (1) состоит из суммы общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения (1).

Чтобы решить однородное линейное уравнение с постоянными коэффициентами (1) надо составить характеристическое уравнение    (2) и найти его корни . Каждому простому корню соответствует частое решение однородного уравнения (1), имеющее вид , а каждому корню кратности k  - решения . Произвольная линейная комбинация всех частных решений является общим решением однородного уравнения (1), т.е. , где произвольные постоянные.
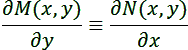