
- •Билет 3
- •Билет 4
- •Билет 9
- •Билет 10
- •Билет 11
- •Билет 12
- •Билет 13
- •14 Билет
- •Билет 15
- •Билет 17 Билет 19
- •Билет 20
- •Билет 21 Теоремы Вейерштрасса для непрерывных функций на отрезке
- •Билет 22
- •Билет 25
- •Билет 26
- •Билет 29
- •Билет 30
- •1. Производная в точке.
- •2. Дифференцируемость в точке.
- •Билет 31
- •Билет 35
- •Билет 36
- •Билет 37
- •Билет 38
- •Формулы асимптотики
Матанализ, 1 курс, 1 семестр, КБ-101, билеты
Билет 3
Единственность предела сходящейся последовательности.
Определение предела:
an
сходится, если найдётся a,
к которому стремится an
![]()
![]()
Теорема:
Если {an} – сходится, то её предел единственный.
Доказательство:
Пусть an→a, an→b>a
ε = (b-a)/3 >0
п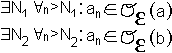 оε
>0
оε
>0
по ε >0
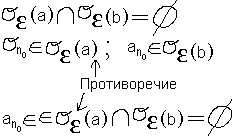
n0>max{N1,N2}=N;N≥N1,N≥N2; (n>N1)^(n>N2)
n0>N1,n0>N2
Определение 1:
![]() при {an}
– ограничено ;an€ [m;M]
при {an}
– ограничено ;an€ [m;M]
Определение 2:
{![]() an}
– ограничено, если
an}
– ограничено, если
О![]() пределение
3:
пределение
3:
{an}– сходится, если
![]()
{an} – ограничена, если
Опр2 =>Опр3
О![]() пр3=> Опр2
пр3=> Опр2
M = max {M0, |a1|, |a2|,…,|an-1|}>0
![]()
Берём
n<N : |an| ≤ M
n≥N : |an| ≤ M0 ≤ M
Билет 4
Теорема об ограниченности
Если {an}- сходится, то {an} – ограничена. Обратное неверно
Доказательство:
ε=1;an→a
п![]() оε>0
оε>0
| an| - |a| ≤ |an - a| < 1
| an| - |a| < 1
| an| < 1 + |a|
{an}ограничена по Опр3
Теорема:
Пусть {an} – монотонна, тогда {an} – ограничена <=> {an} сходится
Доказательство:
Необходимость – следует из теоремы об ограниченности
Достаточность – из теоремы о полноте R(изV)
Билет 5
Теорема о сохранении знака:
an→a>0,
тогда![]()
![]() Доказательство:
Доказательство:
ε = a/2>0 , тогда и an > a/2
Билет 6
Теорема о переходе к пределу в неравенстве для двух последовательностей:
{an},
{bn},![]()
lim an = a, lim bn = b, тогда lim an ≤ lim bn
Доказательство:
От противного:
Пусть a>b
ε = (a-b)/2 > 0
= (a-b)/2 > 0
по ε > 0
по ε > 0
n0 > N = max {N1, N2}; n0 > N1, n0 > N2
an0 > a – ε = a – (a-b)/2 = (a+b)/2 = (2b+a-b)/2 = b+(a-b)/2 = b+ε > bn0
то есть an0 >bn0. Противоречие!
Билет 7
Теорема о 3-х последовательностях:
{an}, {bn}, {cn}
![]() : an
≤ cn
≤ bn
: an
≤ cn
≤ bn
lim an = lim bn = a, тогда cn → a
![]()
Доказательство:
п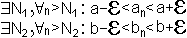 оε> 0
оε> 0
по ε> 0
N = max {N1, N2}
Берём любое n>N ; n>N1, n>N2
a - ε < an ≤ cn ≤ bn < a+ ε, то есть a – ε < cn < a + ε
Билет 8
Связь между бесконечно малыми и бесконечно большими последовательностями.
Определение:
Последовательность
{αn}называется
бесконечно
малой, если
αn→0
при
n→+∞.
Развернутое определение:
![]()
Определение:
Последовательность{βn}
называется бесконечно
большой, если
![]() Этот факт будем записывать так:
Этот факт будем записывать так:
![]() при
при
![]() или
или
![]()
Теорема.
Последовательность
{αn},
(αn
≠ 0) является
бесконечно малой последовательностью
тогда и только тогда, когда последовательность
![]() является
бесконечно большой.
является
бесконечно большой.
Доказательствоследует из того
факта, что неравенство |αn|<εравносильно неравенству
![]() ,
и определений бесконечно малых и
бесконечно больших последовательностей.
(Берем
,
и определений бесконечно малых и
бесконечно больших последовательностей.
(Берем![]() )
)
Билет 9
Свойства бесконечно малых последовательностей:
Сумма и разность бесконечно малых последовательностей
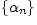 и
и
 есть
бесконечно малая последовательность.Доказательство.Возьмем
произвольное
есть
бесконечно малая последовательность.Доказательство.Возьмем
произвольное
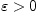 .
Для него
.
Для него
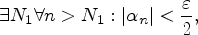
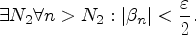 Тогда
Тогда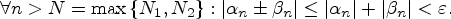
Произведение
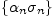 бесконечно
малой последовательности
бесконечно
малой последовательности
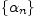 на
ограниченную последовательность
на
ограниченную последовательность
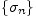 есть
бесконечно малая последовательность.Доказательство.Из ограниченности
есть
бесконечно малая последовательность.Доказательство.Из ограниченности
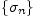 следует
существование числа
следует
существование числа
 такого,
что для всех
такого,
что для всех
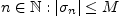 .
Следовательно, при любом положительном
.
Следовательно, при любом положительном
 для
положительного
для
положительного
 существует
номер
существует
номер
 такой,
что для всех
такой,
что для всех
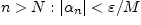 .
Поэтому для этихn>N
имеем
.
Поэтому для этихn>N
имеем .
Следовательно, по определению Коши,
.
Следовательно, по определению Коши,
 при
при
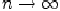 .
.Для того чтобы последовательность
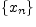 была
сходящейся, необходимо и достаточно,
чтобы существовали число
была
сходящейся, необходимо и достаточно,
чтобы существовали число
 и
бесконечно малая последовательность
и
бесконечно малая последовательность
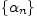 такие,
что для всех
такие,
что для всех
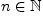 выполнялось
равенство
выполнялось
равенство
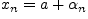 .Доказательство.Необходимость.
Пусть
.Доказательство.Необходимость.
Пусть
 при
при
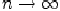 .
Рассмотрим
.
Рассмотрим
 ,
тогда из определения сходимости
,
тогда из определения сходимости
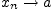 следует,
что
следует,
что
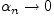 при
при
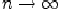 .Достаточность. Если
.Достаточность. Если
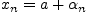 ,
то из того, что
,
то из того, что
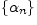 - бесконечно малая последовательность
и
- бесконечно малая последовательность
и
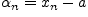 следует,
что
следует,
что
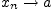 при
при
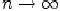 .
.
