
- •18.Предел фнп
- •19.Повторный предел
- •20.Непрерывность ФункцийНесколькихПеременных
- •Дифференциал высшего порядка функции нескольких переменных
- •Замечание
- •Метод множителей Лагранжа для решения задачи условного экстремума Теорема
- •Следствие
- •Достаточное условие условного экстремума
- •Геометрический смысл двойного интеграла
- •Выражение двойного интеграла через полярные координаты
- •61. Ависящий от параметра собственный интеграл
- •Свойства интеграла, зависящего от параметра НепрерывностьПусть функция непрерывна в области как функция двух переменных. Тогда функция непрерывна на отрезке .
- •Интегрирование под знаком интеграла
- •64) Эйлеровы интегралы.Гамма-функция, бета-функция
Метод множителей Лагранжа для решения задачи условного экстремума Теорема
Пусть ![]() —
точка условного экстремума функции
—
точка условного экстремума функции ![]() при
выполнении уравнений связи. Тогда в
этой точке
при
выполнении уравнений связи. Тогда в
этой точке ![]() градиенты
градиенты ![]() являются
линейно зависимыми, то есть
являются
линейно зависимыми, то есть ![]() но
но ![]() .
.
Следствие
Если ![]() —
точка условного экстремума
функции
—
точка условного экстремума
функции ![]() относительно
уравнений связи, то
относительно
уравнений связи, то ![]() такие,
что в точке
такие,
что в точке ![]() или
в координатном виде
или
в координатном виде ![]() .
.
Достаточное условие условного экстремума
Пусть ![]() является
стационарной точкой функции
Лагранжа
является
стационарной точкой функции
Лагранжа ![]() при
при ![]() .
Если
.
Если ![]() —
отрицательно (положительно) определена
квадратическая форма переменных
—
отрицательно (положительно) определена
квадратическая форма переменных![]() при
условии
при
условии ![]() ,
то
,
то ![]() является
точкой max (min для положительно определенной)
условного экстремума. Если она при этих
условиях не является знакоопределенной,
тогда экстремума нет.
является
точкой max (min для положительно определенной)
условного экстремума. Если она при этих
условиях не является знакоопределенной,
тогда экстремума нет.
32.Теорема о неявной функции — общее название для теорем, гарантирующих локальное существование и описывающих свойства неявной функции, т. е. функции
![]() ,
,
![]() ,
,
заданной уравнением
![]() ,
,
![]()
и
значение ![]() фиксированно.
фиксированно.
Одномерный случай
Простейшая теорема о неявной функции состоит в следующем.
|
Если
функция
тогда
найдётся такой двумерный промежуток
|
Обычно
дополнительно предполагается, что
функция ![]() непрерывнодифференцируема,
в этом случае условие монотонности
следует из того, что
непрерывнодифференцируема,
в этом случае условие монотонности
следует из того, что ![]() ,
здесь
,
здесь![]() обозначаетчастную
производную
обозначаетчастную
производную ![]() по
по![]() .
Более того, в этом случае производная
функции
.
Более того, в этом случае производная
функции![]() может
быть вычислена по формуле
может
быть вычислена по формуле

Многомерный случай
Пусть ![]() и
и![]() суть
суть![]() -
и
-
и![]() -мерныеевклидовы
пространства с
фиксированными системами координат,
точки которых соответственно
-мерныеевклидовы
пространства с
фиксированными системами координат,
точки которых соответственно ![]() и
и![]() .
Пусть
.
Пусть![]() отображает
некоторую окрестность
отображает
некоторую окрестность![]() точки
точки![]() в
пространство
в
пространство![]() и
и![]() —
координатные функции (от переменных
—
координатные функции (от переменных![]() )
отображения
)
отображения![]() ,
то есть
,
то есть![]() .
.
Предположим,
что ![]() и
отображение
и
отображение![]() является
является![]() раз
непрерывно дифференцируемым в
окрестности
раз
непрерывно дифференцируемым в
окрестности![]() ,
аякобиан отображения
,
аякобиан отображения ![]() не
равен нулю в точке
не
равен нулю в точке![]() ,
т.е.определитель матрицы
,
т.е.определитель матрицы ![]() не
равен нулю. Тогда существуют
окрестности
не
равен нулю. Тогда существуют
окрестности![]() и
и![]() точек
точек![]() и
и![]() соответственно
в пространствах
соответственно
в пространствах![]() и
и![]() ,
причем
,
причем![]() ,
и единственное отображение
,
и единственное отображение![]() ,
такие, что для всех
,
такие, что для всех![]() выполняетсятождество
выполняетсятождество ![]() .
При этом
.
При этом![]() и
отображение
и
отображение![]() является
является![]() раз
непрерывно дифференцируемым на
раз
непрерывно дифференцируемым на![]() .
.
№33Двойной интеграл
Геометрический смысл двойного интеграла
Двойным
интегралом называют кратный интеграл
с ![]() .
.
 .
Здесь
.
Здесь ![]() —
элемент площади в рассматриваемых
координатах.
—
элемент площади в рассматриваемых
координатах.
В
прямоугольных координатах:  ,
где
,
где ![]() —
элемент площади в прямоугольных
координатах.
—
элемент площади в прямоугольных
координатах.
Геометрический смысл двойного интеграла
Пусть
функция ![]() принимает
в области
принимает
в области ![]() только
положительные значения. Тогда двойной
интеграл
только
положительные значения. Тогда двойной
интеграл  численно
равен объему
численно
равен объему ![]() вертикального
цилиндрического тела, построенного на
основании
вертикального
цилиндрического тела, построенного на
основании ![]() и
ограниченного сверху соответствующим
куском поверхности
и
ограниченного сверху соответствующим
куском поверхности ![]() .
.
Выражение двойного интеграла через полярные координаты
В некоторых случаях двойной интеграл проще считать не в прямоугольных, а в полярных координатах, так как при этом может произойти существенное упрощение вида области интегрирования и всего процесса интегрирования в целом.
Применим теорему о замене переменных. Соответствующее переходу преобразование имеет вид:

Модуль
якобиана отображения равен ![]() .
Таким образом получаем, что
.
Таким образом получаем, что
 .
.
Здесь ![]() является
элементом площади в полярных координатах.
является
элементом площади в полярных координатах.
Свойства двойных интегралов.
Часть свойств двойных интегралов непосредственно вытекает из определения этого понятия и свойств интегральных сумм, а именно:
1.
Если функция f(x, y) интегрируема в D, то
kf(x, y) тоже интегрируема в этой области,
причем ![]() (7.4)
(7.4)
Если в области D интегрируемы функции f(x, y) и g(x, y), то в этой области интегрируемы и функции f(x, y) ± g(x, y), и при этом
![]() (7.5)
(7.5)
3. Если для интегрируемых в области D функций f(x, y) и g(x, y) выполняется неравенство f(x, y) ≤ g(x, y) , то
![]() (7.6)
(7.6)
Докажем еще несколько свойств двойного интеграла:
4.
Если область D разбита на две области
D1 и D2 без общих внутренних точек и функция
f(x, y) непрерывна в области D, то![]() (7.7).
ДоказательствоИнтегральную
сумму по области D можно представить в
виде
(7.7).
ДоказательствоИнтегральную
сумму по области D можно представить в
виде![]() где
разбиение области D проведено так, что
граница между D1 и D2 состоит из границ
частей разбиения. Переходя затем к
пределу при
где
разбиение области D проведено так, что
граница между D1 и D2 состоит из границ
частей разбиения. Переходя затем к
пределу при![]() ,
получим равенство (7.7).
,
получим равенство (7.7).
5. В случае интегрируемости на D функции f(x, y) в этой области интегрируема и функция | f(x, y) |, и имеет место неравенство
![]() (7.8)
(7.8)
Доказательство.
![]() откуда
с помощью предельного перехода
при
откуда
с помощью предельного перехода
при ![]() получаем
неравенство (7.8)
получаем
неравенство (7.8)
6. ![]() где
SD – площадь области D. Доказательство
этого утверждения получим, подставляя
в интегральную сумму f(x, y) ≡ 0.
где
SD – площадь области D. Доказательство
этого утверждения получим, подставляя
в интегральную сумму f(x, y) ≡ 0.
7.
Если интегрируемая в области D функция
f(x, y) удовлетворяет неравенствуm ≤ f(x,
y) ≤ M,то![]() (7.9)
(7.9)
Доказательство проводится предельным переходом из очевидного неравенства
![]()
№34Рассмотрим
область D, ограниченную линиями ![]() x
= a, x = b ( a < b ), где φ1(х) и φ2(х) непрерывны
на [a, b]. Тогда любая прямая, параллельная
координатной оси Оу и проходящая через
внутреннюю точку области D, пересекает
границу области в двух точках: N1 и N2
(рис.1). Назовем такую область правильной
в на-у правлении
оси Оу. Аналогично определяетсяобластьy=φ2(x),
правильная в направлении N2 оси Ох.
Область, правильную в направлении обеих
координатных осей, будем называть просто
правильной.
x
= a, x = b ( a < b ), где φ1(х) и φ2(х) непрерывны
на [a, b]. Тогда любая прямая, параллельная
координатной оси Оу и проходящая через
внутреннюю точку области D, пересекает
границу области в двух точках: N1 и N2
(рис.1). Назовем такую область правильной
в на-у правлении
оси Оу. Аналогично определяетсяобластьy=φ2(x),
правильная в направлении N2 оси Ох.
Область, правильную в направлении обеих
координатных осей, будем называть просто
правильной.
Пусть функция f(x, y) непрерывна в области D. Рассмотрим выражение
![]() ,
(8.1)
,
(8.1)
называемое двукратным интегралом от функции f(x, y) по области D. Вычислим вначале внутренний интеграл (стоящий в скобках) по переменной у, считая х постоянным. В результате получится непрерывная функция от х:
![]()
Полученную
функцию проинтегрируем по х в пределах
от а до b. В результате получим число ![]()
Докажем важное свойство двукратного интеграла.
Теорема 8.1. Если область D, правильная в направлении Оу, разбита на две области D1 и D2 прямой, параллельной оси Оу или оси Ох, то двукратный интеграл по области D будет равен сумме таких же интегралов по областям D1 и D2
![]() .
(8.2)
.
(8.2)
Доказательство.
а) Пусть прямая х = с разбивает D на D1 и D2 , правильные в направлении Оу. Тогда
![]()
![]() +
+
+![]()
б) Пусть прямая y = h разбивает D на правильные в направлении Оу области D1 и D2 (рис.2). Обозначим через M1 (a1, h) и M2 (b1, h) точки пересечения прямой y = h с границей L области D.
Область D1 ограничена непрерывными линиями
1) y = φ1(x);
2) кривой А1М1М2В, уравнение которой запишем
y = φ1*(x), где φ1*(х) = φ2(х) при а ≤ х ≤ а1 и
b1 ≤ x ≤ b, φ1*(х) = h при а1 ≤ х ≤ b1;
3) прямыми x = a, x = b.
Область D2 ограничена линиями y = φ1*(x),
у = φ2(х), а1 ≤ х ≤ b1.
Применим к внутреннему интегралу теорему о разбиении промежутка интегрирования
![]() +
+ ![]()
Представим второй из полученных интегралов в виде суммы:
![]()
![]() +
+ ![]() +
+ ![]() .
.
Поскольку φ1*(х) = φ2(х) при а ≤ х ≤ а1 и b1 ≤ x ≤ b, первый и третий из полученных интегралов тождественно равны нулю. Следовательно,
ID
= ![]()
![]() ,
то есть
,
то есть ![]() .
.
Следствие. Таким же образом можно разбить область D на любое число правильных областей. При этом двукратный интеграл по области D будет равен сумме интегралов по частичным областям.
Замечание 1. Используя теорему 8.1 и теоремы о среднем для определенного интеграла, можно доказать, что для двукратного интеграла справедливы соотношения:
![]()
![]()
![]() (8.3)
(8.3)
где т и М – соответственно наименьшее и наибольшее значение функции f(x, y) в области D, а S – площадь этой области, и
ID = f(P)S, (8.4)
где Р – точка, принадлежащая области D .
Замечание 2. Более употребительной формой записи двукратного интеграла является
![]() =
= ![]() (8.5)
(8.5)
Теорема 8.2. Двойной интеграл от непрерывной функции f(x, y) по правильной области D равен двукратному интегралу от этой функции по данной области, то есть
![]()
![]() (8.6)
(8.6)
Доказательство.
Разобьем область D прямыми, параллельными координатным осям, на п правильных (в основном прямоугольных) областей ΔS1, ΔS2,…, ΔSn. Тогда по теореме 8.1
![]() .
.
Из
(8.4) получим: ![]() ,
где справа стоит интегральная сумма,
предел которой равен двойному интегралу
от f по области D, а слева – постоянное
число ID . Переходя к пределу при
,
где справа стоит интегральная сумма,
предел которой равен двойному интегралу
от f по области D, а слева – постоянное
число ID . Переходя к пределу при ![]() ,
получим равенство (8.6).
,
получим равенство (8.6).
Вопрос №35 Замена переменных в двойном интеграле
Пусть
функция f (x, y)
непрерывна в некоторой замкнутой
ограниченной области G.
Тогда для функции f (x, y)
существует двойной интеграл![]() .
.
Предположим, далее, что с помощью формул x = x(u, v), y = (u, v) мы переходим к новым переменным u и v. Будем считать, что u и v определяются из формул замены переменных единственным образом: u = u (x, y), v = v (x, y). С помощью этих формул каждой точке М(х, у) из области D ставится в соответствие некоторая точка М*(u, v) на координатной плоскости с прямоугольными координатами u и v. Пусть множество всех точек М*(u, v) образуют замкнутую область G*. Прямолинейные координатные линии x = const, y = const разбиения области D в силу приведённой замены переменных u = u(x, y), v = v(x, y) преобразуются в криволинейные. К примеру, декартовые и полярные координаты связаны соотношениями
x = r·cos φ, y = r·sin φ,
и
криволинейными координатными
линиями будут r =
const, φ = const.
По
определению двойного интеграла имеем![]()
Рассмотрим некоторую ячейку разбиения σi,j и найдём его площадь. Так как криволинейная ячейка является бесконечно малой, то её можно приближённо считать совпадающей с параллелограммом, построенном на векторах AB и AC. Известны координаты точек
![]() ,
, ![]() ,
, ![]() ,
,
поэтому координатами указанных выше векторов будут
![]() ,
,
![]() .
.
Найдём векторное произведение этих векторов
 .
.
Как известно, площадь параллелограмма численно равно модулю векторного произведения векторов, построенных на сторонах параллелограмма:
Δ σ i, j ≈ | J | ·Δ ui Δ vj,
где определитель

называется определителем матрицы Якоби. Преобразование двойного интеграла к новым переменным производится по формуле
![]()
Действительно,
![]()
Что и требовалось доказать.
Вопрос №36
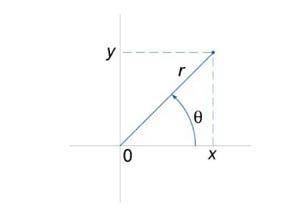
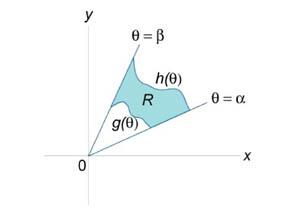
Рис 1 рис 2


Рис 3 рис 4
Одним из частных случаев замены переменных является переход из декартовой в полярную систему координат (рисунок 1).
![]()
Якобиан такого преобразования имеет вид

Следовательно,
дифференциальный элемент в полярных
координатах будет равен![]()
Пусть область интегрирования R в полярных координатах определяется следующим образом (рисунок 2):
![]()
Тогда двойной интеграл в полярных координатах описывается формулой

Будем называть полярным прямоугольником область интегрирования, показанную на рисунке 3 и удовлетворяющую условиям
![]()
В этом случае формула замены переменных в двойном интеграле имеет вид

Будьте внимательны, чтобы не пропустить сомножитель (якобиан) r в правой части этой формулы!
Вопрос №37Геометрические приложения двойных интегралов
Площадь плоской фигуры
Если f (x,y)
= 1 в
интеграле ![]() ,
то двойной интеграл равен площади
области интегрирования R.
Площадь
области типа I (элементарной относительно
оси Оy)
(рисунок 1) выражается через повторный
интеграл в виде
,
то двойной интеграл равен площади
области интегрирования R.
Площадь
области типа I (элементарной относительно
оси Оy)
(рисунок 1) выражается через повторный
интеграл в виде
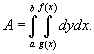
Аналогично, площадь области типа II (элементарной относительно оси Оx) (рисунок 2) описывается формулой




Рис 1 Рис 2 Рис 3
Объем тела
Если f (x,y) > 0 в области интегрирования R, то объем цилиндрического тела с основанием R, ограниченного сверху поверхностью z = f (x,y), выражается формулой
![]()
В
случае, когда R является
областью типа I, ограниченной линиями ![]() ,
объем тела равен
,
объем тела равен

Для
области R типа
II, ограниченной графиками функций ![]() ,
объем соответственно равен
,
объем соответственно равен

Если
в области R выполняется
неравенство ![]() ,
то объем цилиндрического тела между
поверхностями z1 = f (x,y) и z2 = g (x,y) с
основанием R равен
,
то объем цилиндрического тела между
поверхностями z1 = f (x,y) и z2 = g (x,y) с
основанием R равен
![]()
Площадь поверхности
Предположим, что поверхность задана функцией z = f (x,y), имеющей область определения R. Тогда площадь такой поверхности над областью z определяется формулой
![]()
при
условии, что частные производные ![]() и
и ![]() непрерывны
всюду в области R.
непрерывны
всюду в области R.
Площадь и объем в полярных координатах
Пусть S является
областью, ограниченной линиями ![]() (рисунок
3). Тогда площадь этой области определяется
формулой
(рисунок
3). Тогда площадь этой области определяется
формулой
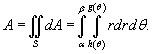
Объем
тела, ограниченного сверху поверхностью ![]() с
основанием S,
выражается в полярных координатах в
виде
с
основанием S,
выражается в полярных координатах в
виде
![]()
Вопрос №38Свойства тройного интеграла. (определение)
Определение тройного интеграла
Формально
определение тройного интеграла можно
ввести аналогично двойному интегралу
как предел суммы Римана. Начнем с
простейшего случая, когда область
интегрирования U имеет
вид параллелепипеда ![]() (рисунок
1).
(рисунок
1).

Рис.1
Пусть множество чисел {x0, x1, ..., xm} разбивает отрезок [a, b] на малые интервалы, так что справедливо соотношение
![]()
Аналогично построим разбиение отрезка [c, d] вдоль оси Oy и [p, q] вдоль оси Oz:
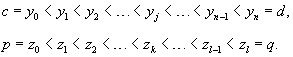
Сумма
Римана функции f (x,y,z) над
разбиением ![]() имеет
вид
имеет
вид
![]()
Здесь (ui , vj , wk) - некоторая точка в параллелепипеде (xi−1, xi)×(yi−1, yi)×(zi−1, zi), а приращения равны
![]()
Тройной
интеграл от
функции f (x,y,z) в
параллелепипеде ![]() определяется
как предел суммы Римана, при котором
максимальное значение
приращений Δxi, Δyj и Δzk стремятся
к нулю:
определяется
как предел суммы Римана, при котором
максимальное значение
приращений Δxi, Δyj и Δzk стремятся
к нулю:

Чтобы
определить тройной интеграл в произвольной
области U,
выберем параллелепипед ![]() ,
включающий заданную область U.
Введем функцию g (x,y,z),
такую, что
,
включающий заданную область U.
Введем функцию g (x,y,z),
такую, что

Тогда тройной интеграл от функции функции f (x,y,z) в произвольной области U определяется в виде:
![]()
Основные свойства тройного интеграла
Пусть функции f (x,y,z) и g (x,y,z) интегрируемы в области U. Тогда справедливы следующие свойства:


 ,
где k -
константа;
,
где k -
константа;Если
 в
любой точке области U,
то
в
любой точке области U,
то 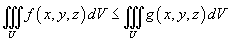 ;
;Если область U является объединением двух непересекающихся областей U1 и U2, то
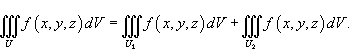 ;
;Пусть m - наименьшее и M - наибольшее значение непрерывной функции f (x,y,z) в области U. Тогда для тройного интеграла справедлива оценка:
![]()
где V - объем области интегрирования U.
Теорема о среднем значении тройного интеграла. Если функция f (x,y,z) непрерывна в области U, то существует точка M0
 U,
такая, что
U,
такая, что
![]()
где V - объем области U.
Вопрос №39Вычисление тройного интеграла в декартовых координатах
Вычисление тройного интеграла в декартовых координатах сводится к последовательному вычислению трех определенных интегралов. Рассмотрим случай, когда область интегрирования U является элементарной относительно оси Oz, т.е. любая прямая, параллельная оси Oz, пересекает границу области U не более, чем в двух точках. Пусть областьU ограничена снизу поверхностью z = z1(x,y), а сверху - поверхностью z = z2(x,y) (рисунок 1). Проекцией телаU на плоскость Oxy является область D (рисунок 2). Будем предполагать, что функции z1(x,y) и z2(x,y)непрерывны в области D.


Рис 1 Рис 2
Тогда для любой непрерывной в области U функции f (x,y,z) можно записать соотношение

Таким образом, вычисление тройного интеграла сводится к вычислению двойного интеграла, в котором подынтегральной функцией является однократный интеграл. В рассмотренном случае сначала вычисляется внутренний интеграл по переменной z, а затем - двойной интеграл в области D по переменным x и y. Если область D(x,y) является областью типа I (смотрите Повторные интегралы), т.е. ограничена линиями
![]()
где f1(x), f2(x) - непрерывные функции в интервале [a,b] и f1(x) ≤ f2(x), то, записывая двойной интеграл в виде повторного, получаем

В другом случае, когда область D(x,y) относится к типу II (является элементарной относительно оси Ox) и ограничена линиями
![]()
где φ1(y), φ2(y) - непрерывные на отрезке [c,d] функции, причем φ1(y) ≤ φ2(y), тройной интеграл представляется в виде

Формулы
(1) и (2) называются формулами
сведения тройного интеграла к
повторному.
В
частном случае, когда область
интегрирования U представляет
собой прямоугольный параллелепипед ![]() ,
тройной интеграл вычисляется по формуле
,
тройной интеграл вычисляется по формуле

Если исходная область интегрирования U более сложная, чем рассмотренная выше, то ее нужно разбить на конечное число более простых областей, в которых уже можно вычислить тройные интегралы методом сведения к повторным.
Вопрос №40Тройной интеграл в цилиндрических координатах
В цилиндрических координатах положение точки M(x,y,z) в пространстве Oxyz определяется тремя числами −ρ, φ, z , где ρ − длина радиуса-вектора проекции точки M на плоскость Oxy, φ − угол, образованный этим радиусом-вектором с осью Ox (рисунок 1), z − проекция на ось Oz (ее значение одинаково в декартовых и цилиндрических координатах).

Рис 1
Цилиндрические координаты точки связаны с ее декартовыми координатами соотношениями
![]()
Здесь предполагается, что
![]()
Якобиан перехода от декартовых координат к цилиндрическим равен

Тогда формула замены переменных при данном преобразовании имеет вид:
![]()
Переход к цилиндрическим координатам упрощает вычисление тройного интеграла в случаях, когда область интегрирования образована цилиндрической поверхностью.
Вопрос №41Тройной интеграл в сферических координатах
Сферическими координатами точки M(x,y,z) называются три числа − ρ, φ, θ , где
ρ −
длина радиуса-вектора точки M;
φ −
угол, образованный проекцией
радиуса-вектора ![]() на
плоскость Oxy и
осью Ox;
θ −
угол отклонения радиуса-вектора
на
плоскость Oxy и
осью Ox;
θ −
угол отклонения радиуса-вектора ![]() от
положительного направления оси Oz (рисунок
1).
от
положительного направления оси Oz (рисунок
1).

Рис 1
Обратите внимание, что определения ρ, φ в сферических и цилиндрических координатах отличаются друг от друга. Сферические координаты точки связаны с ее декартовыми координатами соотношениями

Якобиан перехода от декартовых координат к сферическим имеет вид:

Раскладывая определитель по второму столбцу, получаем

Соответственно, абсолютное значение якобиана равно
![]()
Следовательно, формула замены переменных при преобразовании декартовых координат в сферические имеет вид:
![]()
Тройной интеграл удобнее вычислять в сферических координатах, когда область интегрирования Uпредставляет собой шар (или некоторую его часть) и/или когда подынтегральное выражение имеет видf (x2 + y2 + z2). Иногда выгодно использовать т.н. обощенные сферические координаты, связанные с декартовыми формулами
![]()
В этом случае якобиан равен
![]()
Вопрос №42 Приложения тройного интеграла
Объем тела
![]()
Масса тела
![]()
(![]() -
плотность тела).
-
плотность тела).
Вопрос №43Криволинейные интегралы первого рода
Определение
Пусть
кривая C описывается
векторной функцией ![]() ,
где переменная s представляет
собойдлину
дуги кривой
(рисунок 1).
Если
на кривой C определена скалярная
функция F,
то интеграл
,
где переменная s представляет
собойдлину
дуги кривой
(рисунок 1).
Если
на кривой C определена скалярная
функция F,
то интеграл ![]() называется криволинейным
интегралом первого рода от
скалярной функции F вдоль
кривой C и
обозначается как
называется криволинейным
интегралом первого рода от
скалярной функции F вдоль
кривой C и
обозначается как![]()
Криволинейный
интеграл ![]() существует,
если функция F непрерывна
на кривой C.
существует,
если функция F непрерывна
на кривой C.


Рис 1 Рис 2
Свойства криволинейного интеграла первого рода
Криволинейный интеграл I рода обладает следующими свойствами:
Интеграл не зависит от ориентации кривой;
Пусть кривая C1 начинается в точке A и заканчивается в точке B, а кривая C2 начинается в точкеB и заканчивается в точке D (рисунок 2). Тогда их объединением будет называться криваяC1 U C2, которая проходит от A к B вдоль кривой C1 и затем от B к D вдоль кривой C2. Для криволинейных интегралов первого рода справедливо соотношение
![]()
Если гладкая кривая C задана параметрически соотношением
 и
скалярная функция F непрерывна
на кривой C,
то
и
скалярная функция F непрерывна
на кривой C,
то
![]()
Если C является гладкой кривой в плоскости Oxy, заданной уравнением
 ,
то
,
то
![]()
Если гладкая кривая C в плоскости Oxy определена уравнением
 ,
то
,
то
![]()
В полярных координатах интеграл
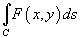 выражается
формулой
выражается
формулой
![]()
где
кривая C задана
в полярных координатах функцией ![]() .
.
Вычисление криволинейного интеграла I рода
Вычисление криволинейного интеграла I рода может быть сведено к вычислению определенного интеграла. Приведем без доказательства правила вычисления криволинейного интеграла I рода в случаях, если кривая L задана параметрическим, полярным и явным образом.
Параметрическое представление кривой интегрирования
Если кривая АВ задана параметрическими уравнениями х=x(t),y=y(t), t[α;β], где x(t) и y(t) — непрерывно дифференцируемые функции параметра t, причем точкеА соответствует t = α, точке В — значение t = β, то

Аналогичная
формула имеет место для криволинейного
интеграла от функции
 (х;у;z)
по пространственной кривой АВ,
задаваемой уравнениями х=x(t),
у
= y(t),
z=z(t),
α≤t
≤β:
(х;у;z)
по пространственной кривой АВ,
задаваемой уравнениями х=x(t),
у
= y(t),
z=z(t),
α≤t
≤β:

Явное представление кривой интегрирования
Если кривая АВ задана уравнением у = φ(x), х [а; b], где φ(x) — непрерывно дифференцируемая функция, то

Подынтегральное
выражение в правой части формулы
получается заменой в левой части
у=φ(х)
и
 (дифференциал дуги кривой).
(дифференциал дуги кривой).
Полярное представление кривой интегрирования
Если
плоская кривая Lзадана
уравнением r—
r
( ),α≤φ≤βв
полярных
координатах, то
),α≤φ≤βв
полярных
координатах, то
 и
и

Подчеркнем, что нижний предел определенного интеграла в формулах должен быть меньше верхнего.
Некоторые приложения криволинейного интеграла I рода
Длина кривой
Длина
Iкривой
АВплоской
или пространственной линии вычисляется
по формуле l
= .
.
Площадь цилиндрической поверхности
Если
направляющей цилиндрической
поверхности служит кривая АВ,лежащая
в плоскости Оху,
а образующая параллельна оси Oz(см.
рис. 235), то площадь поверхности,
задаваемой функцией z = f(x;y),
находится по формуле Q
=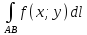 .
.
Масса кривой
Масса
материальной кривой АВ(провод,
цепь, трос,...) определяется формулой
т ,
где γ
= γ(М)
= γ(x;
у)
— плотность АВ
,
где γ
= γ(М)
= γ(x;
у)
— плотность АВ
кривой в точке М.
Статические моменты, центр тяжести
Статические моменты относительно осейОх и Оу и координаты центра тяжести материальной кривой АВ определяются по формулам

Моменты инерции
Для материальной кривойА В моменты IХ, IУ, Iо инерции относительно осей Ох, Оу и начала координат соответственно равны:

КРИВОЛИНЕИНЫИ ИНТЕГРАЛ II РОДА
Основные понятия
Пусть
в плоскости Оху
задана непрерывная кривая АВ
(или L)
и функция Р(х;у),
определенная в каждой точке кривой.
Разобьем кривую АВ
точками
 =
А,
=
А,
 ,...,
Мп
= Вв
направлении от точки А
к точке В
на п
дуг
,...,
Мп
= Вв
направлении от точки А
к точке В
на п
дуг![]() с
длинами Δ
с
длинами Δ (i
= 1,2,...
, п).
(i
= 1,2,...
, п).
На
каждой «элементарной дуге»
![]() возьмем
точку
возьмем
точку![]() и составим сумму вида
и составим сумму вида
Рис. 237

![]() где
где
![]() -
проекция дуги
-
проекция дуги![]() на осьOx
(см. рис. 237). Сумму называют интегральной
суммой для функции Р(х;у) по переменной
х.
Таких сумм можно составить бесчисленное
множество. Если при
на осьOx
(см. рис. 237). Сумму называют интегральной
суммой для функции Р(х;у) по переменной
х.
Таких сумм можно составить бесчисленное
множество. Если при![]() интегральная
сумма имеет конечный предел, не
зависящий ни от способа разбиения кривойАВ,
ни от выбора точек
интегральная
сумма имеет конечный предел, не
зависящий ни от способа разбиения кривойАВ,
ни от выбора точек![]() ,
то его называюткриволинейным
интегралом по координате х
(или II рода) от
функции P(x;y) по кривой AB и обозначают
,
то его называюткриволинейным
интегралом по координате х
(или II рода) от
функции P(x;y) по кривой AB и обозначают
![]()
Итак,
![]()
Аналогично вводится криволинейный интеграл от функции Q(x;у) по координате у:
 где
Δ
где
Δ -
проекция дуги
-
проекция дуги![]() на осиOy.
на осиOy.
Криволинейный интеграл II рода общего вида
![]() определяется
равенством
определяется
равенством
![]()
Криволинейный
интеграл
![]() по пространственной кривойL
определяется аналогично.
по пространственной кривойL
определяется аналогично.
Теорема. Если кривая АВгладкая, а функции Р(х;у)и Q(x;y) непрерывные на кривой АВ,то криволинейный интеграл II рода существует.
Отметим лишь некоторые свойства криволинейного интеграла II рода.
При изменении направления пути интегрирования криволинейный интеграл II рода изменяет свой знак на противоположный, т. е.

(проекция
дуги![]() на
осиОх
и Оу
меняют знаки с изменением направления).
на
осиОх
и Оу
меняют знаки с изменением направления).
Если кривая АВ точкой С разбита на две части АС и СВ, то интеграл по всей кривой равен сумме интегралов по ее частям, т. е.


Если кривая АВ лежит в плоскости, перпендикулярной осиОх, то
Криволинейный интеграл по замкнутой кривой (обозначается
 не зависит от выбора начальной точки
(зависит только от направления обхода
кривой).
не зависит от выбора начальной точки
(зависит только от направления обхода
кривой).
Вычисление криволинейного интеграла II рода
Вычисление криволинейного интеграла II рода, как и I рода, может быть сведено к вычислению определенного интеграла.
Параметрическое представление кривой интегрирования
Пусть
кривая АВ
задана параметрическими уравнениями
х
= x(t)
и
у
= y(t),
где функции x(t)
и y(t)
непрерывны вместе со своими производными
x'(t)
и y'(t)
на отрезке [α; β], причем начальной точке
А
кривой
соответствует значение параметра t
= α,
а конечной точке В
— значение t
= β. И пусть функция Р(х;у)
непрерывна на кривой АВ.
Тогда,
по определению, .![]()
Преобразуем
интегральную сумму к переменной t.
Так как
![]() ,
то
по формуле Лагранжа имеем:
,
то
по формуле Лагранжа имеем:
![]() где
где![]()
![]()
![]()
Выберем
точку
![]() так, чтобы
так, чтобы![]() .
Тогда преобразованная интегральная
сумма
.
Тогда преобразованная интегральная
сумма
Будет
интегральной суммой для функции одной
переменной P(x(t)‘,y(t))-x'(t)
н промежутке [α;β]. Поэтому![]()
Аналогично получаем:
![]()
Складывая
почленно полученные равенства и
получаем:![]()
Явное представление кривой интегрирования
Если
кривая АВ
задана уравнением у
=φ(х),
х
[a;b],
где функция φ(х)
и ее производная φ'(х)
непрерывны на отрезке [а; b],
то из формулы(Складывая почленно
полученные равенства и получаем),
приняв х
за параметр, имеем параметрические
уравнения кривой АВ:
х=х, у=φ(х),
х
[а; b],
откуда получим:![]()
![]()
В частности,
Если АВ — гладкая пространственная кривая, которая описывается непрерывными на отрезке [α;β] функциями х = x(t), у = y(t) и z = z(t), то криволинейный интеграл
![]()
вычисляется
по формуле
Замечание.
Криволинейные интегралы I
и II
рода связаны соотношением,![]() где
α и β
— углы, образованные касательной к
кривой АВ
в точке М{х;у)
с осямиОх
и Оу
соответственно.
где
α и β
— углы, образованные касательной к
кривой АВ
в точке М{х;у)
с осямиОх
и Оу
соответственно.
Формула Остроградского-Грина
Пусть на плоскости Оху задана область D, ограниченная кривой, пересекающейся с прямыми, параллельными координатным осям не более чем в двух точках, т. е. область D — правильная.
Теорема.
Если
функции Р(х;у)
и Q(x;y)
непрерывны вместе со своими частными
производными
![]() и
и![]() в
областиD,
то имеет место формула
в
областиD,
то имеет место формула![]() (
Остроградского-Грина)
(
Остроградского-Грина)
где L — гранив области D и интегрирование вдоль кривой L производится в положительном направлении (при движении вдоль кривой, область D остается слева).
Пусть
у
= φ(х)
— уравнение дуги АпВ,
а у
= φ2(х)
— уравнение дуги АтВ
(см. рис.). Найдем сначала![]() По
правилувычисления
двойного интеграла, имеем:
По
правилувычисления
двойного интеграла, имеем:

Или,
согласно формуле,
![]() Аналогично доказывается, что
Аналогично доказывается, что![]() Замечание.
Формула Грина справедлива и для
произвольной области, которую можно
разбить на конечное число правильных
областей.
Замечание.
Формула Грина справедлива и для
произвольной области, которую можно
разбить на конечное число правильных
областей.
Работа переменной силы
Переменная
сила F(P(x;у);
Q{x;у))
на криволинейном участке АВ
производит
работу, которая находится по формуле
![]()
Действительно, пусть материальная точка (х; у) под действием переменной силы F перемещается в плоскости Оху по некоторой кривой АВ (от точкиА до точки В).
Разобьем
кривую АВ
точками
 =А,
=А, ,М2,...,Мп=В
на п
«элементарных» дуг
,М2,...,Мп=В
на п
«элементарных» дуг
![]() длины Δ
длины Δ и в каждой из них возьмем произвольную
точку
и в каждой из них возьмем произвольную
точку![]() ,
i
= 1; 2 ;...;п
(см. рис.). Заменим каждую дугу
,
i
= 1; 2 ;...;п
(см. рис.). Заменим каждую дугу![]() вектором
вектором![]() ,
а
силу F
будем считать постоянной на векторе
перемещения
,
а
силу F
будем считать постоянной на векторе
перемещения![]() и
равной заданной силе в точке
и
равной заданной силе в точке дуги
дуги![]() :
:
![]() Тогда
скалярное произведение
Тогда
скалярное произведение
![]() можно
рассматриватькак приближенное значение
работыFi
вдоль дуги
можно
рассматриватькак приближенное значение
работыFi
вдоль дуги
![]() :
:
![]() Приближенное
значение работыА
силы F
на всей кривой составит величину
Приближенное
значение работыА
силы F
на всей кривой составит величину
![]() За точное значение работыА
примем предел полученной суммы при
За точное значение работыА
примем предел полученной суммы при
![]() (тогда,
очевидно,
(тогда,
очевидно, и
и ):
):
![]()
Условия независимости криволинейного интеграла II рода от пути интегрирования
Теорема
.Для
того чтобы криволинейный интеграл
![]() не
зависел от пути интегрирования в
односвязной областиD,в
которой функции Р(х;у),
Q(x;y)непрерывны
вместе со своими частными производными,
необходимо и достаточно, чтобы в каждой
точке этой области выполнялось условие
не
зависел от пути интегрирования в
односвязной областиD,в
которой функции Р(х;у),
Q(x;y)непрерывны
вместе со своими частными производными,
необходимо и достаточно, чтобы в каждой
точке этой области выполнялось условие![]()
Докажем
достаточность условия. Рассмотрим
произвольный замкнутый контур АтВпА
(или L)
в области D
(см. рис.). Для него имеет место формула
Остроградского-Грина (56.8). В силу условия
(56.12) имеем:
![]() или
или![]()

Учитывая свойства криволинейного интеграла, имеем:
 т.е.
т.е.
![]()
Полученное равенство означает, что криволинейный интеграл не зависит от пути интегрирования.
Площадь плоской фигуры
Площадь
S
плоской фигуры, расположенной в плоскости
Оху
и ограниченной замкнутой линией L,
можно найти по формуле
![]() при этом криваяL
обходится против часовой стрелки.
при этом криваяL
обходится против часовой стрелки.
Док-во: Действительно, положив в формуле Остроградского-Грина Р(х;у) = 0, Q(x;y) = х, получим:
![]() или
или
![]() (1)
(1)
Аналогично,
полагая P
= —у, Q=
0, найдем еще одну формулу для вычисления
площади фигуры с помощью криволинейного
интеграла:
![]() (2)
(2)
Сложив
почленно равенства (1) и (2) и разделив на
два, получим:
![]()
ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ I РОДА
Если
при![]() интегральная
сумма
интегральная
сумма![]() имеет предел, то он называетсяповерхностным
интегралом I
рода
от функции f(x;y;z)по
поверхности S
и обозначается
имеет предел, то он называетсяповерхностным
интегралом I
рода
от функции f(x;y;z)по
поверхности S
и обозначается
![]() .
.![]()
Таким образом, по определению,
Вычисление
Вычисление поверхностного интеграла I рода сводится к вычислению двойного интеграла по области D — проекции поверхности S на плоскость Оху.
Разобьем
поверхность S
на части Si,
i
= 1;п.
Обозначим через σiпроекцию
Si
на плоскость Оху.
При этом область D
окажется разбитой на п
частей σ1,σ
2,
...,σ
п.
Возьмем в σi,
произвольную точку Pi(xi;yi)
и восстановим перпендикуляр к плоскости
Оху
до пересечения с поверхностью
S.Получим
точку Mi{xi;yi;zi)
на поверхности Si.
Проведем в точке Mi
касательную плоскость и рассмотрим ту
ее часть Ti,
которая на плоскость Оху
проектируется в область σi
(см. рис.). Площади элементарных частей
Si,
Ti
и σi
обозначим как ΔSi,
ΔТi;
и Δσi;
соответственно. Будем приближенно
считать, что![]() (2)
(2)
(57.3)
Обозначив
через γi
острый угол между осью Ozи
нормалью ni
к поверхности в точке Мi,
получаем:
![]() (1)
(1)
(область
σi
есть проекция Ti
на плоскость Оху).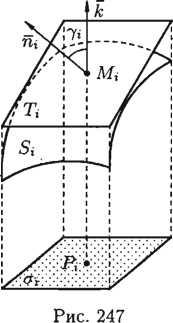
Если
поверхность S
задана уравнением z
= z(x;y),то,
уравнение касательной плоскости в точке
Мi
есть![]()
где
z'x(xi;yi),
z'y(xi;yi),-1
— координаты нормального вектора к
плоскости. Острый угол γi
есть угол между векторами к
=
(0;
0;
1)
и![]()
Следовательно,![]()
Равенство
(1) принимает вид![]() В правой части формулы заменимΔSi
(учитывая (2)) на полученное выражение
для ΔТ,azi
заменим на z(xi;yi).
Поэтому, переходя к пределу при
стремлении к нулю наибольшего диаметра
Si
(а следовательно, и σi),
получаем формулу
В правой части формулы заменимΔSi
(учитывая (2)) на полученное выражение
для ΔТ,azi
заменим на z(xi;yi).
Поэтому, переходя к пределу при
стремлении к нулю наибольшего диаметра
Si
(а следовательно, и σi),
получаем формулу
![]() выражающую
интеграл по поверхности S
через двойной интеграл по проекции S
на плоскость Оху.
выражающую
интеграл по поверхности S
через двойной интеграл по проекции S
на плоскость Оху.
Отметим,
что если поверхность S
задана уравнением вида у
= у(х;z)
или х
= х(у;z),
то аналогично получим:
![]() и
и![]()
где D1 и D2 — проекции поверхности S на координатные плоскости Oxz и Oyz соответственно.
Приложения
Площадь поверхности
Если поверхность S задана уравнением z = z(x; у), а ее проекция на плоскость Оху есть область D, в которой z(x;y), zx'(x;y) и zy'(x;y) — непрерывные функции, то ее площадь S вычисляется по формуле
![]() или
или
![]()
Моменты, центр тяжести поверхности
Статистические моменты, координаты центра тяжести, моменты инерции материальной поверхности 5 находятся по соответствующим формулам:

Двусторонние и односторонние поверхности.
Двусторонняя поверхность (таковой является плоскость, эллипсоид, любая поверхность, задаваемая уравнением z = f(xжy), где f(x;y),fх' и fy' — функции, непрерывные в некоторой области D плоскости Оху и т. д.). Примером односторонней поверхности является так называемый лист Мебиуса, получающийся при склеивании сторон АВ и CD прямоугольника ABCD так, что точкаА совмещается с точкой С, а В — с D (см. рис.).
![]()
ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ II РОДА
Предел
интегральной суммы
![]() при
при![]() ,
если он существует и не зависит от
способа разбиения поверхностиS
на части Si
и от выбора точек МiSi,
называется поверхностным
интегралом II
рода
(по координатам) от функции f(x;y;z)
по переменным х
и упо
выбранной стороне поверхности и
обозначается
,
если он существует и не зависит от
способа разбиения поверхностиS
на части Si
и от выбора точек МiSi,
называется поверхностным
интегралом II
рода
(по координатам) от функции f(x;y;z)
по переменным х
и упо
выбранной стороне поверхности и
обозначается
![]()
Итак,
![]()
Аналогично определяются поверхностные интегралы II рода по переменным у и z и z и х:

Общим видом поверхностного интеграла II рода служит интеграл
 где
P,
Q,
R
— непрерывные функции, определенные в
точках двусторонней поверхности S.
где
P,
Q,
R
— непрерывные функции, определенные в
точках двусторонней поверхности S.
53. Формула Стокса

обход
контура ![]() (границы
поверхностиS)
согласован с выбором стороны поверхности S.
(границы
поверхностиS)
согласован с выбором стороны поверхности S.
Формула Стокса в символической форме


(![]() -
направляющие косинусы нормали,
соответствующей выбранной стороне
поверхности.
-
направляющие косинусы нормали,
соответствующей выбранной стороне
поверхности.
54.
Формула
Остроградского—Гаусса устанавливает
связь между поверхностным интегралом
по замкнутой ориентированной поверхности
G и тройным интегралом по пространственной
области![]()
![]() =
G, и обобщает формулу Грина на
пространственный случай. Т: Пусть функции
P(x,y,z), Q(x,y,z), R(x,y,z) непрерывны вместе со
своими частными производными первого
порядка в ограниченной замкнутой
области
=
G, и обобщает формулу Грина на
пространственный случай. Т: Пусть функции
P(x,y,z), Q(x,y,z), R(x,y,z) непрерывны вместе со
своими частными производными первого
порядка в ограниченной замкнутой
области![]() =
G — гладкая ориентированная поверхность.
Тогда справедлива формула
=
G — гладкая ориентированная поверхность.
Тогда справедлива формула
![]() (27.9)
(27.9)
причем поверхностный интеграл берется по внешней стороне G
Формула (27.9) и носит название формулы Остроградского— Гаусса.
Предположим,
что![]() —
простая область, т.е.
—
простая область, т.е.![]() пересекается
с любой прямой, параллельной осям
координат, не более чем в двух точках
(рис. 27.10). Если
пересекается
с любой прямой, параллельной осям
координат, не более чем в двух точках
(рис. 27.10). Если![]() не
является простой, то ее необходимо
разбить на конечное число простых
областей. Пусть
не
является простой, то ее необходимо
разбить на конечное число простых
областей. Пусть![]() —
уравнения нижней
—
уравнения нижней![]() и
верхней
и
верхней![]() поверхностей
G, D=
поверхностей
G, D=![]() G.
Тогда, используя (27.8), имеем
G.
Тогда, используя (27.8), имеем
![]()


55. Условия независимости криволинейного интеграла (второго рода) от формы пути интегрирования
Пусть функции P(x, y, z), Q(x, y, z) и R(x, y, z) непрерывны в некоторой области D пространства XYZ. Будем рассматривать в этой области только кусочно-гладкие кривые.
Возьмем
в области D две
произвольные точки А и В. Их можно
соединять различными кривыми, лежащими
в области D.
По каждой из этих кривых интеграл ![]() имеет,
вообще говоря, свое значение.
имеет,
вообще говоря, свое значение.
Вычислим,
например, интеграл ![]() по
отрезку прямой АВ, соединяющему точки
А(1, 0, 0) и В(1, 1, 1)
по
отрезку прямой АВ, соединяющему точки
А(1, 0, 0) и В(1, 1, 1)
Уравнения
прямой АВ: ![]() т.е.
x = 1, y = z.
т.е.
x = 1, y = z.
Выбирая
за параметр y, имеем:![]()
Вычислим теперь тот же интеграл по дуге параболы АВ, заданной уравнениями
x
= 1, z = y2. Выбирая за параметр y (x =
1, y = y, z = y2, yA =
0, yB =
1), получим:![]()
Этот
пример показывает, что значения
интеграла ![]() зависят
от формы кривой, по которой производится
интегрирование.
зависят
от формы кривой, по которой производится
интегрирование.
Можно, однако, привести примеры криволинейных интегралов, значения которых по любым кривых, соединяющим данные точки А и В, будут одни и те же. Такими, как можно показать, являются интегралы:
![]()
![]() и
др.
и
др.
Будем
говорить, что интеграл ![]() в
областиD не
зависит от формы пути интегрирования,
если его значения по всевозможным
кусочно-гладким кривым, лежащим в данной
области и имеющим общее начало и общий
конец, одинаковы. В этом случае при
записи интеграла достаточно указывать
лишь начальную и конечную точки пути
интегрирования, в связи с чем приняты
обозначения:
в
областиD не
зависит от формы пути интегрирования,
если его значения по всевозможным
кусочно-гладким кривым, лежащим в данной
области и имеющим общее начало и общий
конец, одинаковы. В этом случае при
записи интеграла достаточно указывать
лишь начальную и конечную точки пути
интегрирования, в связи с чем приняты
обозначения:![]()
![]() или
или ![]()
Независимость
криволинейного интеграла ![]() в
областиD от
формы пути интегрирования равносильна
равенству нулю этого интеграла, вдоль
всякой замкнутой кривой L,
лежащей в области D
в
областиD от
формы пути интегрирования равносильна
равенству нулю этого интеграла, вдоль
всякой замкнутой кривой L,
лежащей в области D
56. Если в каждой точке рассматриваемой области W заданная величина принимает числовые значения, то поле называется скалярным, если же в каждой точке области W задан вектор, то поле называется векторным.
Если
существует предел отношения (1), когда
точка ![]() ,
двигаясь по выбранной прямой s,
приближается к
,
двигаясь по выбранной прямой s,
приближается к ![]() ,
то он называется производной скалярного
поля
,
то он называется производной скалярного
поля ![]() в
точке
в
точке ![]() по
направлению
по
направлению ![]() и
обозначается
и
обозначается ![]() .
Таким образом, производная по направлению
есть
.
Таким образом, производная по направлению
есть
![]() .
.
Определение
производной (4.2) по направлению
вектора ![]() при
условии
при
условии ![]() характеризует
скорость изменения поля
характеризует
скорость изменения поля ![]() в
направлении этого вектора и не
связано с выбором какой-либо системы
координат.
в
направлении этого вектора и не
связано с выбором какой-либо системы
координат.
В
декартовой системе координат производная
по направлению ![]() вычисляется
по формуле
вычисляется
по формуле
![]() ,
(3)
,
(3)
где a, b, g -
углы, образуемые вектором ![]() с
осями координат
с
осями координат
Градиентом скалярного
поля ![]() в
точке
в
точке![]() называется
вектор, проекция которого на
направление заданного единичного
вектора равна производной поля
называется
вектор, проекция которого на
направление заданного единичного
вектора равна производной поля![]() по
этому направлению
по
этому направлению
![]() . (6)
. (6)
2. Производная по направлению принимает свое наибольшее значение в направлении градиента

57.
Дивергенция – это характеристика
векторного поля, инвариантная относительно
системы координат.дивергенция
векторного поля в точке M
имеет смысл объемной плотности потока
векторного поля через окрестность этой
точки и характеризует мощность источника
(если
 >0)
или стока (если
>0)
или стока (если <0)
векторного поля в точкеM.
<0)
векторного поля в точкеM.
Векторное
поле
 называетсясоленоидальным
в области V,
если в любой точке M
этой области
называетсясоленоидальным
в области V,
если в любой точке M
этой области


Назовем
ротором
векторного поля
 вектор
вектор

Векторное
поле
 называетсяпотенциальным,
если существует такое скалярное поле
называетсяпотенциальным,
если существует такое скалярное поле
 (потенциал
векторного поля
(потенциал
векторного поля
 ),
что
),
что =
= .
.
Замечание.
Если поле
 - потенциально, то
- потенциально, то
 =
= -
полный дифференциал. Тогда
-
полный дифференциал. Тогда -
полный дифференциал. Поэтому свойства
потенциального поля можно сформулировать
и доказать как следствия теоремы о
полном дифференциале.
-
полный дифференциал. Поэтому свойства
потенциального поля можно сформулировать
и доказать как следствия теоремы о
полном дифференциале.
Оператор
Гамильтона
 .
.
Применим
оператор Гамильтона к скалярному полю
 .
.
Оператор
Гамильтона представляет собой
вектор-оператор. Его можно скалярно или
векторно умножить на векторное поле
 .
.

Это дифференциальные операции первого порядка над скалярным и векторным полями. От скалярного поля можно взять градиент, от векторного поля можно взять дивергенцию и ротор.
Дифференциальные операции второго порядка.
В
результате дифференциальных операций
первого порядка мы получаем скалярные
и векторные поля
 .
.
К ним вновь можно применить дифференциальные операции первого порядка.
От
скалярного поля
 можно
взять градиент, получив векторное поле
можно
взять градиент, получив векторное поле .
.
От
векторных полей
 можно
взять ротор и дивергенцию, получив
скалярные поля
можно
взять ротор и дивергенцию, получив
скалярные поля ,
,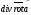 и
векторные поля
и
векторные поля ,
, .
.
Итак,
дифференциальные операции второго
порядка позволяют получить скалярные
поля
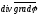 ,
, и векторные поля
и векторные поля ,
, ,
, .
.
Ранее
было показано, что потенциальное
поле – безвихревое,
т.е.
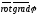 =0.
=0.
58. Циркуляцией векторного поля называется линейный интеграл по замкнутому контуру.
 .
.
Вводя эти понятия, можно записать формулу Стокса в «полевой» форме
 .
.
59.
![]() через поверхность S
определяется как интеграл по S:
через поверхность S
определяется как интеграл по S:
![]() ,
,
где ![]() —
проекция вектора поля нанормаль к
поверхности,
—
проекция вектора поля нанормаль к
поверхности, ![]() —
«векторный элемент поверхности»,
определяемый, как вектор единичной
нормали, умноженный на
—
«векторный элемент поверхности»,
определяемый, как вектор единичной
нормали, умноженный на![]() .
Простейшим примером этой конструкции
является объём жидкости, проходящий
через поверхностьS,
при её течении со скоростью F.
.
Простейшим примером этой конструкции
является объём жидкости, проходящий
через поверхностьS,
при её течении со скоростью F.
Формулу Остроградского – Гаусса можно записать в «полевом» виде
 -
поток векторного поля через замкнутую
поверхность
-
поток векторного поля через замкнутую
поверхность
 равен объемному интегралу от дивергенции
поля по области, ограниченной поверхностью
равен объемному интегралу от дивергенции
поля по области, ограниченной поверхностью .
.
60.
Для того чтобы функциональный ряд
 равномерно
сходился в области V,
необходимо и достаточно, чтобы
равномерно
сходился в области V,
необходимо и достаточно, чтобы
 .
.
