
- •18.Предел фнп
- •19.Повторный предел
- •20.Непрерывность ФункцийНесколькихПеременных
- •Дифференциал высшего порядка функции нескольких переменных
- •Замечание
- •Метод множителей Лагранжа для решения задачи условного экстремума Теорема
- •Следствие
- •Достаточное условие условного экстремума
- •Геометрический смысл двойного интеграла
- •Выражение двойного интеграла через полярные координаты
- •61. Ависящий от параметра собственный интеграл
- •Свойства интеграла, зависящего от параметра НепрерывностьПусть функция непрерывна в области как функция двух переменных. Тогда функция непрерывна на отрезке .
- •Интегрирование под знаком интеграла
- •64) Эйлеровы интегралы.Гамма-функция, бета-функция
61. Ависящий от параметра собственный интеграл
Пусть
в двумерном евклидовом
пространстве задана
область ![]() ,
на которой определена функция
,
на которой определена функция ![]() двух
переменных.
двух
переменных.
Пусть
далее, ![]() .
.
Функция ![]() и
называется интегралом,
зависящим от параметра.
и
называется интегралом,
зависящим от параметра.
Свойства интеграла, зависящего от параметра НепрерывностьПусть функция непрерывна в области как функция двух переменных. Тогда функция непрерывна на отрезке .
Доказательство
Рассмотрим
приращение интеграла, зависящего от
параметра. ![]()
![]() .
.
По теореме
Кантора,
непрерывная на компакте функция равномерно
непрерывна на
нём, то есть ![]()
![]() .
.
Следовательно, ![]() при
при ![]() ,
что и означает непрерывность функции
,
что и означает непрерывность функции
Дифференцирование под знаком интеграла
Пусть
теперь на области ![]() непрерывна
не только функция
непрерывна
не только функция ![]() ,
но и её частная производная
,
но и её частная производная ![]() .
.
Тогда ![]() ,
или, что то же самое,
,
или, что то же самое, ![]()
Доказательство![]()
![]() Данные
преобразования были выполнены с
использованиемтеоремы
о среднем Лагранжа.
Рассмотрим теперь выражение
Данные
преобразования были выполнены с
использованиемтеоремы
о среднем Лагранжа.
Рассмотрим теперь выражение ![]() .
.
Используя
вновь теорему Кантора, но для функции ![]() мы
получаем, что
мы
получаем, что![]() при
при![]() ,
что и доказывает данную теорему
,
что и доказывает данную теорему
Интегрирование под знаком интеграла
Если
функция ![]() непрерывна
в области
непрерывна
в области ![]() ,
то
,
то
![]() ,
или, что то же самое:
,
или, что то же самое:
![]()
62. Несобственные интегралы, зависящие от параметра.
определение
Пусть имеется функция f(x; l), которая определена и непрерывна при x и l, таких что .
При этом , так что промежуток x Î [a; b] является конечным;
, так что промежуток l Î [a; b] может быть и бесконечным.
Если функцию f(x; l) проинтегрировать по промежутку x Î [a; b], то получим функцию,
которая называется интегралом, зависящим от параметра λ.
63. Га́уссовинтегра́л (также интеграл Э́йлера — Пуассо́на или интеграл Пуассона[1]) — интеграл от гауссовой функции:
![]()
Гауссовы интегралы от масштабированной гауссовой функции
![]()
и многомерные гауссовы интегралы
![]()
элементарно сводятся к обычному одномерному, описанному первым (здесь и ниже везде подразумевается интегрирование по всему пространству).
То же относится к многомерным интегралам вида
![]()
где x — вектор, а M — симметричная матрица с отрицательными собственными числами, так как такие интегралы сводятся к предыдущему, если сделать преобразование координат, диагонализующее матрицу М.
Практическое
применение (например, для вычисления
Фурье-преобразование от гауссовой
функции) часто находит следующее
соотношение![]()
64) Эйлеровы интегралы.Гамма-функция, бета-функция
Бета-функцией
Эйлера называется интеграл
![]() .
.
Гамма-функцией
Эйлера называется интеграл![]()
Свойства B функции:
Область определения
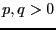 .
Доказательство. Разобъем интеграл на
сумму двух интегралов точкой
.
Доказательство. Разобъем интеграл на
сумму двух интегралов точкой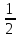 .
Тогда при
.
Тогда при выполнено
выполнено .
Но интеграл
.
Но интеграл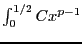 сходится. Аналогично доказывается для
второго интеграла.
сходится. Аналогично доказывается для
второго интеграла.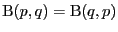 Доказательство
через замену переменных.
Доказательство
через замену переменных. Формулы понижения
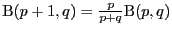 .
Доказательство.
.
Доказательство.
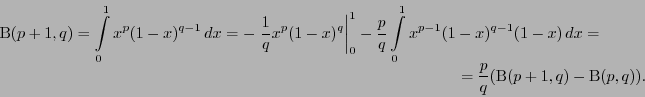
После выполнения переноса в левую часть и деления на соответствующий множитель получим требуемое равенство.
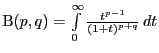 получаетсязаменой
получаетсязаменой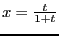
СвойстваГфункции:
Область определения
 .
Доказательство. Разобъем интеграл на
сумму двух интегралов точкой 1. Тогда
приx[0,1]
выполнено
.
Доказательство. Разобъем интеграл на
сумму двух интегралов точкой 1. Тогда
приx[0,1]
выполнено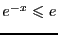 .
Но интеграл
.
Но интеграл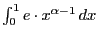 сходится. На
сходится. На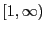 имеем
имеем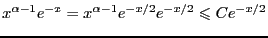 .
А
.
А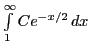 сходится.
сходится.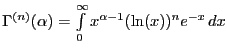 .
Доказательство. Воспользуемся теоремой
о возможности дифференцирования под
знаком несобственного интеграла: если
есть функция
.
Доказательство. Воспользуемся теоремой
о возможности дифференцирования под
знаком несобственного интеграла: если
есть функция то если интеграл сходится равномерно
вG,
то
то если интеграл сходится равномерно
вG,
то
 .
То есть нам нужно доказать равномерную
сходимость Г(α)
по α. Для этого возьмем на (0,1] и [1,
.
То есть нам нужно доказать равномерную
сходимость Г(α)
по α. Для этого возьмем на (0,1] и [1,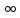 )
мажорантные интегралы
)
мажорантные интегралы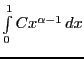 и
и .
Они сходятся, значит исходный сходится
равномерно. Тогда можно дифференцировать.
Дифференцируя по α подинтегральное
выражение, получим требуемое.
.
Они сходятся, значит исходный сходится
равномерно. Тогда можно дифференцировать.
Дифференцируя по α подинтегральное
выражение, получим требуемое.Формулы понижения
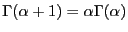 .
Доказательство
.
Доказательство
![]()
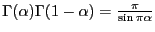
Г(1)=1, Г(n+1)=n!, Г(
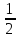 )=
)=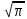 ,
Г(n+
,
Г(n+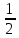 )=(n-1)!
)=(n-1)!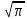 .
Доказательство.Первые два равенства
доказываются непосредственно подсчетом
интегралов и применением формулы
понижения, последнее через формулу
понижения. Третье равенство - частный
случай свойства 4 при α=
.
Доказательство.Первые два равенства
доказываются непосредственно подсчетом
интегралов и применением формулы
понижения, последнее через формулу
понижения. Третье равенство - частный
случай свойства 4 при α=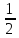 .
.
Cвязь
между Гамма- и Бетта-функциями (без
доказательства):
![]()
406
