итог3

72

7. (cosu)' = -sin u ×u';

8. (tgu)' =

1

×u';

cos2 u

1

1

9. (ctgu)'

= -

×u' ;

10. (arcsinu)' =

×u' ;

sin 2 u

1-u2

11. (arccosu)' =

-1

×u' ;

12. (arctgu)' =

1

×u' ;

1

+ u2

1- u2

13. (arcctgu)' = -

1

×u' ;

14. (shu)' = chu ×u';

1+ u2

1

15. (chu)' = shu ×u';

16. (thu)' =

×u' ;

ch2u

1

17. (cthu)' = -

×u'.

sh2u

Примеры.

æ

ö'

æ

æ

ö1/ 3 ö'

æ

ö−2 / 3 æ

ö'

'

(x

3

+1)

x

3

+

1

1

x

3

+1

x

3

+1

а) y

=

ç

3

÷

=

ç

ç

÷

÷

=

ç

÷

ç

÷

=

ç

(x

3

-1)

÷

ç

ç

3

-

1

÷

÷

3

ç

3

-1

÷

×ç

3

-1

÷

1

è

ø

è

è x

ø

ø

è x

ø

è x

ø

1

(x3 +1)(x3 -1)- (x3 +1)(x3 -1)

'

'

=

×

×

=

3

(x3 -1)2

æ

x

3

+

1

ö2

3

ç

÷

3

ç

-

1

÷

è x

ø

=

(x3 -1)2 / 3

×

3x2 (x3

-1)- (x3 +1)3x

2

=

3(x3 +1)2 / 3

(x3 -1)2

(x3 -1)2 / 3

×

3x2 (-2)

= -

2x2

;

3(x3 +1)2 / 3

(x3 -1)2

3 (x2 +1)2 (x3 -1)4

б) y' = êé(2x4 - tg4x)3 úù'

= 3(2x4

- tg4 x)2 ×(2x4 - tg4 x)' =

ë

û

= 3(2x4 - tg4x)2 × êé(2x4 )' - (tg4 x)' úù =

ë

û

f (x)

73

x4

4

2

æ

x4

3

3

1 ö

= 3(2

- tg

x)

×ç2

×ln 2

×

4x

- 4tg

x ×

÷

=

cos2

è

x ø

x4

4

2 æ

x4

3

tg3x

ö

=12(2 - tg x)

×

ç

2 ×ln 2

× x -

÷

2

ç

cos

x

÷

è

ø

Если зависимость между переменными y и x задана в неявном виде f(x,y)=0, то для нахождения производной в простейших случаях достаточно продифференцировать обе части уравнения f(x,y)=0, y, считая функцией от x, и из полученного уравнения, линейного относительно y′ , найти производную.

Логарифмической производной функции y=f(x) называется производная

от логарифма этой функции, т.е.

[ln f (x)]¢ = f ′(x) .

Последовательное применение логарифмирования и дифференцирования функций называют логарифмическим дифференцированием.

Пример. Найти производную функцию y′ , если x3 + y3 - 3xy = 0.

Решение. Дифференцируем обе части данного уравнения, считая y функ- цией от x:

3x2 + 3y2 × y¢ - 3y - 3xy¢ = 0; y¢(3y2 - 3x)= 3y - 3x2;

y¢ = 3y - 3x2 . 3y2 - 3x

Пример. Найти производную функции y = (sin 2x)x3 . Решение. Логарифмируя данную функцию, получаем

ln y = x3 ×ln(sin 2x).

Дифференцируя обе части последнего равенства по x,

(ln y)¢ = (x3 )′ ln(sin 2x)+ x3 ×(ln(sin 2x))¢;

отсюда

yy′ = 3x2 ×ln(sin 2x) + x3 × sin12x ×cos 2x × 2;

74

y¢ = y(3x2 ×ln(sin 2x) + 2x3ctg2x);

y¢ = (sin 2x)x3 [3x2 ×ln(sin 2x) + 2x3 ×ctg2x].

Производной второго порядка или второй производной функции y=f(x)

называется производная от ее первой производной, т.е. (y¢)′ .

Обозначается вторая производная одним из следующих символов:

y¢¢, f ¢¢(x), d2 y . dx2

Производной n–го порядка функции y=f(x) называется производная от производной (n–1)–го порядка данной функции.

Если зависимость функции y от аргумента x задана в параметрическом

dy

=

y′(t)

,

d2 y

=

d

æ

y¢ ö

×

1

, где

виде уравнениями x=x(t), y=y(t), то:

ç

÷

dx

x¢(t)

dx2

x¢

dt è

x¢ ø

штрих обозначает производную по t.

Пример. Найти производную второго порядка y = ln(x + 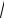x2 + a2 ).

Решение.

¢

′

1

′

2

2

2

2

y

= (ln(x + x

+ a )) = x + x2 + a2

×(x + x + a ) =

æ

ö

1

x

x2 + a2 + x

ç

÷

=

=

(x +

)×

x +

x

2

+ a

2

×ç1+

x

2

+ a

2

÷

x

2

+ a

2

x

2

+ a

2

è

ø

=

1

x2

+ a2

ö′

æ

1

1

2

2

−

3

x

¢¢

ç

÷

2

y

= -

(x

+ a

)

×2x = -

= ç

x

2

+ a

2

÷

2

3 .

è

ø

(x2 + a2 )

функции

=

Пример. Найти производную функции, заданной параметрическими уравнениями: x=lnt, y = t3 + 2t +1.

75

Решение.

dy = 3t2 + 2 = 3t3 + 2t; dx 1

t

Геометрически производная функции f(x) в т. x0 равна тангенсу угла на- клона касательной, проведенной к графику функции в точке с абсциссой x0 с положительным направлением оси Оx.

f ′(x0 ) = tgα .

Так как tgα называется угловым коэффициентом касательной, то мож- но записать tgα = k , т.е. f ′(x0 ) = k. Тогда уравнение касательной, как уравнение прямой, проходящей через т. M (x0; y0 ) с угловым коэффициен- том k = f ′(x0 ) , может быть записано в виде y - y0 = k(x - x0 ) .

	Пример. Составить		уравнение	касательной к гиперболе x × y =1
	в т. x0 =1.
					¢		1
	Решение.	Здесь	x0 =1,	f (x0 )= f (1) =1,		(x)= - x2 ,
					f
	k = f ′(1) = -1.	Подставим найденные значения в уравнение касательной
	y -1 = -(x -1),	y = 2 - x .

Уравнение нормали (перпендикуляра) к кривой

	M (x , f (x )) имеет вид			y - y = -	1		(x - x ),
					f ¢(x0 )
	0	0	0	0			0

f ′(x0 ) = 0 , уравнение нормали имеет вид x = x0 ).

Пример. Записать уравнение нормали к кривой

т. с абсциссой x=1.
Решение. x0 =1;	f (x0 ) = f (1) = -8.
f ′(x) = 2x -16,	f ′(x0 ) = f ′(1) = -14.

y = f (x) в	точке
f ′(x0 ) ¹ 0	(если

y = x2 -16x + 7 в

	Тогда y + 8 = -	1	×(x -1); y =		1	x - 8	1	.
		-14		14			14

Рассмотрим применение производной к вычислению некоторых преде-

лов.

76

Правило Лопиталя.

Пусть функции

f (x)

и

g(x) непрерывны и дифференцируемы на не-

котором отрезке

[a,b]

и

обращаются

в

нуль

в

т.

x = a ,

т.е.

f (a) = g(a) = 0 ,

тогда,

если

существует предел отношения

f ′(x)

при

¢

g (x)

x → a , то существует и lim

f (x)

, причем lim

f (x)

= lim

f ′(x)

.

x→a

g(x)

x→a g(x)

x→a g¢(x)

x

æ

x

ö′

1

x

çsin

÷

sin 2

é0

ù

2

2 cos 2

1

Пример. lim

=

= lim

è

ø

= lim

=

.

ê

ú

(5x)¢

x→0 5x

x→0

x→0

5

10

ë0

û

При необходимости это правило может быть применено многократно.

Пример.

cos x -1

é0

ù

- sin x

é0

ù

- cos x

1

lim

= ê

ú

= lim

= ê

ú

= lim

= -

.

x

2

0

2x

0

2

2

x→0

ë

û

x→0

ë

û

x→0

Правило Лопиталя применимо и для раскрытия неопределенностей вида

é¥ êë¥

ùú.

û

		ln sin 3x	é¥		ù		3cos3xsin x
	Пример. lim		= ê		ú	= lim		=1.
		ln sin x		¥			sin 3x cos x
	x→0		ë		û	x→0

Пусть тело движется по прямой по закону S = S(t) . За промежуток

времени	t (от момента t	до момента t + t ) оно пройдет некоторый путь
S . Тогда отношение DS		есть средняя скорость движения за промежуток
	Dt
времени	t .
Скоростью движения тела в данный момент времени t называется пре-
дел отношения приращения пути S к приращению времени t , когда при-

ращение времени стремится к нулю:		DS
V (t) = lim Vcp	= lim		¢
		Dt	= S (t).
t→0	t→0

Следовательно, производная пути S по времени t равна скорости пря- молинейного движения тела в данный момент времени t :

77

V (t) = S'(t).

	Скорость протекания физических, химических и других процессов также
выражается с помощью производной.		y = f (x) .	Дадим x приращение
	Рассмотрим произвольную функцию
x , тогда приращение функции равно		y = f (x +	x) − f (x). Отношение
y	- называется средней скоростью изменения этой функции на отрезке Dx .
x

Скоростью изменения функции y = f (x) в точке x называется предел отношения приращения функции Dy к приращению аргумента Dx , когда приращение аргумента стремится к нулю:

V (x) = lim	y	= y′(x).
x→0	x

Итак, скорость изменения функции в точке x равна производной функ- ции в этой точке.

Если тело движется прямолинейно по закону S = S(t) , то вторая произ-

водная пути S по времени t равна ускорению движения тела в данный мо- мент времени t :

a(t) =V ′(t) = S′′(t).

Таким образом, первая производная характеризует скорость некоторого процесса, а вторая - ускорение того же процесса.

Пусть функция y = f (x) непрерывна при рассматриваемых значениях x и имеет производную

			lim	y =	f ′(x).
		y	x→0	x
	Из этого следует, что		= f ′(x) +α , где α - бесконечно малая вели-
		x
	чина при Dx ® 0 . Отсюда находим, что Dy = f ′(x)Dx +α ×Dx.
	Дифференциалом функции y = f (x)				называется главная часть ее при-

ращения, линейная относительно приращения Dx независимой переменной. I. Дифференциал функции y = f (x) обозначается dy .

Итак, dy = f ′(x)Dx.

Положив y = x , получим dx = x′×Dx =1×Dx = Dx , и поэтому

78

dy = f ′(x) × dx

При достаточно малом dx = Dx приращение функции приближенно равно ее дифференциалу, Dy » dy.

Таким образом, f (x + Dx) » f (x) + dy.

Эта формула позволяет использовать дифференциал функции для при- ближенных вычислений значений функций.

Применение производной при исследовании функций

Пределы и производные удобно применять к исследованию функций и построению графиков.

Общая схема исследования функций и построения их графиков:

1.Найти область определения функции.

2.Найти точки разрыва функции и ее односторонние пределы в этих

точках.

3.Выяснить, является функция четной, нечетной или периодической.

4.Найти точки пересечения графика функции с осями координат и ин- тервалы знакопостоянства функции.

5.Найти асимптоты графика функции:

а) вертикальные; б) невертикальные.

6. Найти точки экстремума и интервалы возрастания и убывания функ-

ции.

7.Найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.

8.Построить график функции, используя все полученные результаты ис- следования.

Рассмотрим отдельно некоторые пункты исследования.

Асимптотой кривой называется такая прямая, к которой неограниченно приближается точка кривой при неограниченном удалении этой точки от на- чала координат.

Для нахождения асимптот пользуются следующими положениями:

а) если при x = a кривая y = f (x)		имеет бесконечный разрыв, т.е. ес-
ли при x → a слева или справа функция		f (x) стремится к бесконечности
(того или иного знака),	то прямая x = a является ее вертикальной асимпто-
той;		y = f (x) , если они существуют,
б) невертикальные асимптоты кривой
имеют уравнения вида	y = kx + b , где параметры k и b определяются

x → −∞

79

	формулами:	f (x)
	k = lim		, b = lim [f (x) - kx].
		x
	x→±∞				x→±∞
	Пример. Найти асимптоты кривой			x2	- 6x + 3	.
					x -3

Решение:

а) при x = 3 кривая имеет бесконечный разрыв. Поэтому прямая x = 3 есть вертикальная асимптота. Найдем односторонние пределы:

- слева	lim	x2		- 6x + 3	= +¥;
				x -3
x→3−0
- справа	lim		x2 - 6x + 3			= -¥;
				x -3
	x→3+0
Значит,	при стремлении x → 3 слева функция неограниченно воз-

растает, а справа - неограниченно убывает; б) найдем невертикальные асимптоты:

k = lim

x→∞

x	2	- 6x + 3	æ	x	2	- 6x + 3	ö
			ç				÷	= -3.
	(x -3)x		=1, b = limç			x - 3	- x÷
			x→∞è				ø

Уравнение невертикальной, наклонной асимптоты будет y = x − 3. Других невертикальных асимптот кривая не имеет, так как при

значения k,b будут те же самые.

Возрастание и убывание функции y = f (x) характеризуется знаком ее производной y' : если в некотором интервале y'> 0 , то функция возрастает, а если y'< 0 , то функция убывает в этом интервале.

Значение функции f (x) в точке x0 называется максимумом (миниму- мом), если оно является наибольшим (наименьшим) по сравнению с ее значе- ниями во всех достаточно близких точках слева и справа от x0 . Функция f (x) может иметь экстремум (максимум или минимум) только в тех точках,

которые лежат внутри области определения функции и где ее первая произ- водная равна нулю или не существует. Такие точки называются критически- ми.

Функция будет иметь экстремум в тех точках, где ее производная y' ме- няет свой знак, а сама функция непрерывна.

80

Из определений вытекает правило исследования функции на экстремум:

1.Найти производную y' и критические точки, лежащие внутри области определения функции.

2.Определить знак y' слева и справа от каждой критической точки. Ес-

ли при переходе аргумента x через критическую точку x0 :

1)y' меняет знак с + на -, то x0 есть точка максимума;

2)y' меняет знак с - на +, то x0 есть точка минимума;

3)y' не меняет знак, то в этой точке нет экстремума.

Для исследования критических точек, где y'= 0 , можно также рас- смотреть знак второй производной:

1)если y"(x0 ) > 0 , то x0 есть точка минимума;

2)если y"(x0 ) < 0 , то x0 есть точка максимума;

3)если y"(x0 ) = 0 , то характер точки x можно выяснить только по из- менению знака y' этой точки.

Пример. Найти интервалы монотонности функции y = (1− x2 )3 и точки

экстремума.

Область определения функции есть множество всех действительных чи-

сел.

y'= ((1− x2 )3 )′ = −6x(1− x2 )2.

Полагая y'= 0 , получим x1 = 0, x2 = −1, x3 = 1. Других критических

точек нет.

Исследуем критические точки по изменению знака первой производной. Составим таблицу:

x	(−∞;−1)	−1	(−1;0)	0	(0;1)	1	(1;∞)
y'	+	0	+	0	-	0	-
y	возрастает	нет	возрастает	максимум	убывает	нет	убывает
		экстр.				экстр.

В первой строке размещены критические точки и интервалы моно- тонности функции. Во второй - знаки производной в интервалах и значения в критических точках. В третьей - выводы о поведении функции.

Соответственно результатам исследования функция возрастает на интер-

81

вале (−∞,0) и убывает на интервале (0,∞) . Точка x = 0 есть точка мак-

симума.

Если в некотором интервале кривая расположена ниже любой своей ка- сательной, то кривая называется выпуклой, а если она расположена выше лю- бой своей касательной, то вогнутой.

Точкой перегиба называется точка на кривой, разделяющая области вы- пуклости и вогнутости.

Характер кривой y = f (x) определяется знаком второй производной y": если в некотором интервале y"> 0 , то кривая вогнутая, а если y"< 0 ,

то кривая выпуклая.

Нахождение точек перегиба и интервалов выгнутости и выпуклости сво- дится к следующему:

1.Найти вторую производную y". В области определения функции и не- прерывности кривой найти точки x , в которых y"= 0 или не существует.

2.Определить знак y" слева и справа от каждой из этих точек. Ис-

следуемая точка x будет абсциссой точки перегиба, если по разные стороны от нее y" имеет разные знаки.

Интервалы выпуклости и вогнутости кривой определяются из условия, что их границами могут быть только точки перегиба, точки разрыва и гра- ничные точки области расположения кривой.

Пример. Найти точки перегиба и интервалы выпуклости и вогнутости кривой y =1- ln(x2 + 4) .

Область определения функции есть множество всех действительных чи-

сел.

2x

æ

2(x2

+ 4)- 2x ×2x ö

2x2 -8

y'= -

, y"= -ç

÷ =

,

x

2

+ 4

(x

2

+ 4)

(x

2

+ 4)

è

ø

ç

2

÷

2

y"= 0 точках x1 = -2; x2 = 2.

Других точек, которые могут быть абсциссами точек перегиба, нет. Исследуем найденные точки, определяя знак y" слева и справа от каж-

дой из них. Составим таблицу:

x	(−∞;−2)	− 2	(−2;2)	2	(2;∞)
y"	+	0	-	0	+
y	вогнута	т.перегиба	выпукла	т.перегиба	вогнута

Рассмотрим пример полного исследования функции и построения ее гра-