итог3

62

Тема 3. ВВЕДЕНИЕ В АНАЛИЗ. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

Программный объем темы

1.Предел, непрерывность функции, основные свойства пределов, беско- нечно малые и бесконечно большие. Замечательные пределы. Сравнение бес- конечно малых. Эквивалентные бесконечно малые. Вычисление пределов с различными видами неопределенностей.

2.Определение производной, ее геометрический и механический смысл. Непрерывность и дифференцируемость. Основные правила нахождения про- изводных. Дифференциал функции. Производные и дифференциалы высших порядков.

3.Применение пределов и производных к исследованию функций и по- строению их графиков. Правило Лопиталя и его применение к вычислению пределов.

3.1.ВВЕДЕНИЕ В АНАЛИЗ

Пусть функция f(x) определена в окрестности некоторой точки х=а, за исключением, быть может, самой точки а.

Определение (на языке «ε − δ »). Число А называется пределом функ-

ции f(x) при

x → a , если для

любого ε >0 можно

указать такое

δ = δ (ε) >0,

что для всех

х,

удовлетворяющих

соотношениям

0 <

x − a

< δ , имеет место неравенство

f (x) − A

< ε .

Тот факт, что А есть предел f(х) при x → a , записывают в виде

lim f (x) = A .

x→a

Если х<а (х>а) и x → a , то пишут x → a –0 ( x → a +0). В первом случае говорят, что X стремится к а слева, во втором случае – справа.

Определение (на языке «ε − δ »). Число A называется пределом функции f(х) при x → a –0, если для любого ε > 0 найдется такое δ > 0, что для всех X, удовлетворяющих соотношениям a − δ < x < a , имеет место не- равенство f (x) − A < ε .

Аналогично определяется предел функции f(х) при x → a справа. Тот факт, что функция f(х) при x → a слева и справа имеет своими пределами

числа А– и A+; записывают в виде lim	f (x) = A , lim	f (x) = A .
x→a−	− x→a+	+

Данные пределы обозначают также символами f(а–0), f(а+0).

Пусть функция f(х) определена для всех х, достаточно больших по абсо- лютной величине ( x > K ).

63

Определение (на языке «ε − δ »). Число А называется пределом функ- ции f(x) при x → ∞ , если для любого ε >0 можно указать число М (М>К),

такое, что для всех |х| > М выполняется неравенство f (x) - A < ε .

Обозначение: lim f (x) = A . Подобным образом вводятся пределы при

x→∞

x → +∞ , x → −∞ .

По аналогии со случаями конечных пределов (А - конечно) можно ввести пределы:

lim f (x) = +¥ ,		lim f (x) = -¥ ,
x→a		x→a
lim	f (x) = +¥ ,	lim f (x) = -¥ ,
x→+∞		x→+∞
lim	f (x) = +¥ ,	lim f (x) = -¥ .
x→−∞		x→−∞

Например,	lim f (x) = -¥ обозначает, что при любом заданном отри-
	x→+∞
цательном числе N существует такое число M>0, что f(x)<N, если x>M.
	Основные свойства пределов.
Пусть lim f (x) = A , lim g(x) = B , где А и В - конечные числа.
x→a	x→a

Тогда

1.lim[ f (x) ± g(x)] = A ± B ,

x→a

2.lim[ f (x) × g(x)] = A× B ,

x→a

3. lim	f (x)	=	A	(при условии, что B ¹ 0 ).
			B
x→a g(x)

При решении задач полезно помнить таблицу простейших пределов:

lim		c		= ¥ ,	lim cx = ¥ ,
x→0		x			x→∞
lim		x		= ¥ ,	lim ax = 0,a <1,
x→∞ c					x→+∞
lim ax = 0,a > 1,					lim ax = +¥,a >1,
x→−∞					x→+∞
lim		c		= 0 ,	lim ax = +¥,a <1,
x→∞ x					x→−∞
lim		loga x = -¥,a >1,			lim loga x = +¥,a > 1.
x→0+0					x→+∞

64

В таблице а>0, c ¹ 0.

Технически проще всего находится предел элементарной функции f(x) при x ® x0 , если x0 принадлежит области определения этой функции. Такой

предел равен f(x0). Ниже приведены основные положения, объясняющие этот результат.

Определение. Класс функций, включающий в себя многочлены, рацио- нальные функции, показательные, степенные, логарифмические, тригономет- рические и обратные тригонометрические функции, а также функции, полу-

чающиеся из перечисленных с помощью четырех арифметических действий и суперпозиций (образование сложной функции), примененных конечное число раз, называют элементарными функциями.

	Например, y =	ecos x3	- 8	, y =	e− x + ex	, y =	2x3 + 3x2 - x +1		,
		sin 4x			2		4x2 - x + 21

y=tglncos3x2 принадлежат к классу элементарных функций.

Теорема. Любая элементарная функция непрерывна в каждой точке сво- ей области определения.

Теорема. Под знаком непрерывной в данной точке Х0 функции f(х) воз-

можен предельный переход в этой точке:

lim

f (x) = f (lim x) = f (x0 ) .

x→x0

x→x0

Пример. lim

x2

+ 2x -1

= -

1

.

x3 + 2

2

x→0

При вычислении пределов необходимо уметь раскрывать (решать) неоп-

ределенности.

¥

0

Определение. Выражения вида

,

,

¥ × 0 , 1∞ , ∞ − ∞ принято на-

¥

0

зывать неопределенностями и обозначать, заключая в квадратные скобки:

	é	¥	ù	é	0	ù	, [¥ × 0], [1∞ ], [¥ - ¥].
	ê ú			, ê		ú
					0
	ë	¥	û	ë		û

Далее на примерах рассматриваются приемы раскрытия основных типов неопределенностей.

При отыскании предела отношения двух целых многочленов отно- сительно х при x → ∞ полезно предварительно разделить оба члена отно- шения на хn, где п - наивысшая степень этих многочленов.

65

Пример.

3x4

x2

1

3x4 - x2 +1

é¥

ù

4 -

+

x

x

4

x

4

lim

= ê

ú

= lim

=

x

4

+10x

x

4

x

→∞

ë¥

û

x→∞

+

10x

x4

1

1

x4

3 -

+

= lim

x2

x4

= 3.

x→∞

1+

10

x3

Пример.

1

6

2

1

x5 - 6x4 + 2x -1

é¥

ù

-

+

-

x

2

5

6

lim

=

ê

ú = lim

x

x

x

= 0..

x

6

- x

5

¥

x

→∞

ë

û

x→∞

1

1-

Пример.

x

1

1

1

4x4

- x2 + x +1

é

¥ù

4 -

+

-

2

3

4

lim

= ê

ú

= lim

x

x

x

= ¥. .

x -

2

x

→∞

ë

¥û

x→∞

1

-

2

Пример.

x3

x4

3 ö3

ö2

æ

2 +

æ

-

2

(2x + 3)3(3x - 2)2

é¥ù

ç

÷ ç3

÷

2332

è

x ø è

x

ø

lim

=

ê

ú

= lim

=

= 72.

x

5

+ 5

5

1

x→∞

ë¥û

x→∞

1+

x5

Аналогичный прием во многих случаях можно применять и для дробей, содержащих иррациональности.

2x + 3

é¥ù

2 +

3

x

Пример. lim

= ê ú

= lim

= 2.

3

x→∞ x +

x

ë¥û

x→∞

+ 3

1

1

x2

Если P(x) и Q(x) – многочлены и P(a)=Q(a)=0, то при отыскании предела

lim[P(x) / Q(x)]

рекомендуется разделить один или несколько раз числи-

x→a

							66
тель и знаменатель на (x-a).
Пример.
	x2	+ 6x + 8	é¥	ù			x2 + 6x + 8		(x + 2)(x + 4)
lim			= ê	ú	=	x1	= -2, x2 = -4	= lim			=
		x + 2							(x +	2)
x→−2			ë¥	û				x→−2

= lim (x + 4) = 2.

x→−2

Выражения, содержащие иррациональности, во многих случаях приво- дятся к рациональному виду путем введения новой переменной.

	x2	-		x	é0			ù
Пример. Найти lim						= ê		ú.
							0
x→1		x -1			ë			û

Введем новую переменную y = 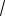x.

Тогда lim	x2 -			x	= lim	y( y3 -1)	= lim y(y2 + y +1) = 3.
						y -1
x→1		x -1			x→1		x→1

Другим приемом нахождения предела от иррационального выражения является перевод иррациональности из числителя в знаменатель или, наобо-

рот, из знаменателя в числитель.
			-		é0			ù
		x + h		x					(x > 0).
Пример. Найти lim						= ê		ú
		h					0
h→0					ë			û

Умножим числитель и знаменатель на выражение	x + h	+			x	,		со-
пряженное с числителем.
Первый замечательный предел удобно представить в виде lim			sinυ					=1,
	x→0			υ

где υ – функция независимой переменной x и υ → 0 - при x → 0.

Первый замечательный предел может быть использован для раскрытия

	é	0	ù
	неопределенностей вида ê		ú.
		0
	ë		û
				1- cos x			=		é0		ù
	Пример. Найти предел lim								ê		ú.
				x	2
			x→0					x	ë0		û
	Учитывая формулу 1	- cos x = 2sin2							, находим:
							2

67

2

x

æ

x

ö2

1- cos x

2sin

1

ç sin

÷

1

2

2

lim

= lim

=

lim

ç

÷ =

.

x2

x

2

x→0

x2

x→0

2 x→0

ç

÷

ç

÷

2

è

ø

arcsin 2x

é0

ù

Пример. Найти предел lim

= ê

ú.

5x

x→0

ë0

û

sin z

Введем новую переменную z: z=arcsin2x. Тогда sinz=2x, x =

и

arcsin 2x

z

2

1

2

2

lim

= lim

=

=

.

5 lim sin z

x→0

5x

z →0 5 sin z

5

2

z →0

z

1

lim(1+υ)

= e , если

Второй замечательный предел запишем в виде

υ

1 υ

x→0

υ → 0 при x → 0;

или lim(1+

= e ,

если υ → ∞ при x → ∞ . Здесь

)

υ

x→∞

υ –

функция независимой переменной x. Полезно также помнить пределы

1

= eα ,

lim(1+ α )υ

= eα , где α = const .

lim(1+αυ)

υ

x→0

x→∞

υ

Второй замечательный предел может быть использован для раскрытия неопределенности [1∞ ].

Пример. limæ x + 5 ö3x = [1∞ ]. x→∞èç x -1 ø÷

Используем известный прием деления «уголком» многочлена x+5 на многочлен x-1.

x+5 x-1

x-1 1

6

Значит, xx+-15 =1+ x6-1 .

68

6

×3x

é

x-1

ù

æ

6

ö

3x

6

ö

x-1

æ

6

18

lim ç1+

÷

= lim

êç1

+

÷

ú

= e .

x -1

x

-1

x®+¥è

ø

x®+¥

êè

ø

ú

ë

û

Пример. Найти

lim (x + 3)[ln( x +1) - ln( x - 2)]= [¥ - ¥].

x®+¥

Учитывая свойства логарифмов, находим

1 öx+3

æ

1

+

lim (x + 3)[ln( x +1) - ln(x - 2)]= lim ln

ç

x

÷

ç

÷

=

2

x®+¥

x®+¥

ç

1

-

÷

ç

÷

è

x ø

é

æ

1+

1

öx+3 ù

é

æ

+

1

öx

æ

+

1 ö3

ù

ê

ç

x

÷

ú

ê

lim ç1

x

÷ ç1

x

÷

ú

= lnê lim

ç

÷

ú = lnê

x®+¥è

ø è

ø

ú

=

- 2 öx

2 ö3

êx®+¥ç

1-

2

÷

ú

ê

æ

æ

ú

ê

ç

÷

ú

ê lim

ç1+

÷ ç1-

÷

ú

x

x

ë

è

ø

û

ë x®+¥è

ø è

x ø

û

= ln

e ×1

= ln e

3

= 3.

e-2 ×1

lim f (x), то

Замечание.

Если

существует

и

положителен

lim[ln f (x)]= ln lim f (x) .

x®a

x®a

x®a

Полезно также помнить и другие замечательные пределы.

lim

loga

(1+ x)

= loga

e,

lim

ax -1

= ln a,

lim

(1+ x)a -1

= a.

x

x

x

x®0

2cos 2 x -1

x®0

x®0

=

é

0ù

Пример.

lim

ê

ú.

ln sin x

x®π

ë

0û

2

Введя замену переменной y=cos2x, находим:

2cos 2 x -1

2y -1

2y

-1

lim

= lim

=

2lim

y

=

ln sin x

1 ln(1- y)

ln(1

- y)

x® 2

y®0

y®0

π

2

y

69

2y -1

= -2lim

y

= -2lim

ln 2

= -2ln 2.

ln[1+ (-y)]

y→0

y→0 ln e

(-y)

ex + e− x

=

é

0ù

Пример.

lim

ê

ú.

sin x

0

x→0

ë

û

lim

ex - e−x

= lim

e2x -1

= lim

e2x -1

×

x

×

2

=

sin x

×ex

2x

sin x

ex

x→0

x→0 sin x

x→0

= 2lim

e2x -1

×lim

x

×lim

1

= 2.

2x

sin x

ex

x→0

x→0

x→0

Определение.

Функция

α = α(x) называется бесконечно

малой при

x → a , если

lim α (x) = 0.

x→∞

Пусть α(x)

и β (x) являются бесконечно малыми функциями при

x → a .

Если

при

этом

их

отношение

стремится

к единице

(lim[α(x) / β (x)]=1), то бесконечно малые α(x) и β (x) называют экви-
x→a
валентными малыми и пишут α(x) ~ β (x) ( x → a ).
Примеры эквивалентных бесконечно малых функций при x → 0:
				ü
sin x ~ x				ï
tgx ~ x				ï	ln(1+ x) ~ x					ü
				ï
arcsin x ~ x				ï	a	x	-1~ x ln a			ï
				ý						ý
arctgx ~ x				ï	(1+ x)			m		ï
	1			ï					-1 ~ mxþ
1- cos x ~		x	2	ï
				ï
	2
				þ

m=const.

При отыскании предела отношения двух бесконечно малых функций ка- ждую из них можно заменить эквивалентной бесконечно малой функцией.

70

	arcsin 5x			é0		ù
Пример. lim				= ê		ú.
	3	2x	-1		0
x→0				ë		û

lim

arcsin 5x

= lim

5x

=

5

.

2ln 3

x→0 32x -1

x→0 2x ln 3

Пример.

lim(1- e2x )ctgx = [0×¥].

x→0

lim(1- e

2x

)ctgx = lim

1- e2x

= lim

- 2x

= -2.

tgx

x

x→0

x→0

x→0

3.2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ

ОДНОЙ ПЕРЕМЕННОЙ

Определение. Предел отношения приращения функции y к прираще-

нию аргумента x

при произвольном стремлении x к нулю называется

производной функции y=f(x) в точке x и обозначается одним из следующих

символов: y’, f’(x),				dy	.
	dy			dx		y		f (x +	x) − f (x)
y'= f '=			= lim				= lim			.(1)
	dx					Dx			Dx
				x→0			x→0

Если указанный в формуле (1) предел существует, то функцию f(x) назы- вают дифференцируемой в точке x, а операцию нахождения производной y’ – дифференцированием.

Пример. Найти производную функции y = 3x2+x 1 , воспользовавшись

определением производной.
Решение. При любом приращении х имеем:
		Dy =	2(x + Dx)		-		2x		=
			3(x + Dx) +1			3x +1
=	6x2	+ 2x + 6xDx + 2Dx - 6x2					- 2x - 6xDx			=
		[3(x + Dx) +1](3x +1)

=	2 x
		.
	(3x +1+ 3Dx)(3x +1)

					71
	Так как Dy		=		2	, то
				(3x +1+ 3Dx)(3x +1)
	Dx
	y'= lim	Dy	= lim		2		=	2	.
		Dx			(3x +1+ 3Dx)(3x +1)			(3x +1)2
	x→0			x→0

Справедливы следующие правила дифференцирования, где С – постоянное число, U(x) и V(x) –некоторые дифференцируемые функции.

1.(C)’=0;

2.(x)’=1;

3.(U ± V)=U’ ± V’;

4.(C×U)’=C×U’;

5.(U×V)’=U’×V+U×V’;

æU ö'

U ' ×V -U ×V '

6.

ç

÷

=

,(V ¹ 0) ;

V 2

è V ø

æ C ö'

-C

'

7. ç

÷

=

V 2

×V

,(V ¹ 0) .

èV ø

8.

Если

y = f (u),u = ϕ(x) , т.е. y = f (ϕ(x)) – сложная функция, со-

ставленная из дифференцируемых функций, то

y' = y'

×u' или

dy

=

dy

×

du

;

x

u

x

dx

du dx

9.

Если для функции

y = f (x) существует обратная дифференцируемая

функция,

x = g( y) и

dg

= g' ( y) ¹ 0 , то f ' (x) =

1

.

dy

g' (y)

На основании определения производной и правил дифференцирования можно составить таблицу производных основных элементарных функций:

α

'

α −1

¢

u '

u

'

1. (u

) = αu

2.

(a ) = a

×ln a ×u ;

×u ;(α Î R) ;

3.

(eu )' = eu ×u' ;

4.

(loga u)'

=

1

×u';

u ×ln a

1

5.

(ln u)' =

×u' ;

6.

(sin u)' = cosu ×u' ;

u