2.5.3. Достаточность условий Куна–Таккера

Теорема 2. Пусть целевая функция f(x) выпуклая, все ограничения в виде неравенств содержат вогнутые функции g_j(x), j=1,2,…,I, а ограничения в виде равенств содержат линейные функции h_k(x), k=1,2,…K. Тогда если существует решение (x^*,U^*,), удовлетворяющее условиям Куна–Таккера, то x^* - оптимальное решение задачи нелинейного программирования.

Если условия теоремы 2 выполняются, то нахождение точки Куна–Таккера обеспечивает получение оптимального решения задачи нелинейного программирования. В качестве иллюстрации опять рассмотрим следующий пример.

Минимизировать при ограничениях

С помощью теоремы 2 докажем, что решение является оптимальным. Для этого необходимо рассмотреть следующие понятия.

Функция n переменных f(x) называется выпуклой функцией тогда и только тогда, когда для любых двух точек x₁ и x₂ , принадлежащих множеству Д, и выполняется неравенство:

Матрица Гессе для функции f(x) есть симметричная матрица порядка nn:

.

Функция f(x) выпуклая, если ее матрица Гессе положительно определена или положительно полуопределена для всех значений x₁, x₂, …x_n, т.е. диагональные элементы должны быть больше 0. Функция f(x) выпуклая, если ее матрица Гессе отрицательно определена или отрицательно полуопределена для всех значений x₁, x₂, …x_n.

Для данной задачи имеем

и .

Так как матрица H_f(x) положительно определена при всех х, функция f(x) оказывается выпуклой. Первое ограничение в виде неравенства содержит линейную функцию g₁(x), которую можно считать вогнутой. Для того чтобы показать, что функция g₂(x) является вогнутой, вычислим

и .

Поскольку матрица отрицательно определена, функцияg₂(x) является вогнутой. Функция h₁(x) входит в линейное ограничение в виде равенства. Следовательно, все условия теоремы 2 выполнены. Если показать, что x^* =(1; 5) - точка Куна–Таккера, то действительно установится оптимальность решения x^*.

Условия Куна–Таккера для данного примера имеют вид:

Точка x^* =(1; 5) удовлетворяет ограничениям (2.13)-(2.15) и, следовательно, является допустимой. Уравнения (2.11) и (2.12) принимают следующий вид:

Положив , получимU₂=0,1 и U₁=2,2. Таким образом, решение x^* =(1; 5), и U^* =(2.2 ,0.1) и удовлетворяет условиям Куна–Таккера. Поскольку условия теоремы 2 выполнены, тоx^* =(1; 5) – оптимальное решение. Заметим, что существуют так же и другие значения U₁, U₂ и , которые удовлетворяют системе уравнений (2.11)-(2.18).

Рассмотрим пример.

Требуется минимизировать

при ограничениях

Составим уравнения, входящие в состав условий Куна–Таккера.

1. Функция Лагранжа имеет вид

откуда: .

2. Условия дополняющей нежесткости:

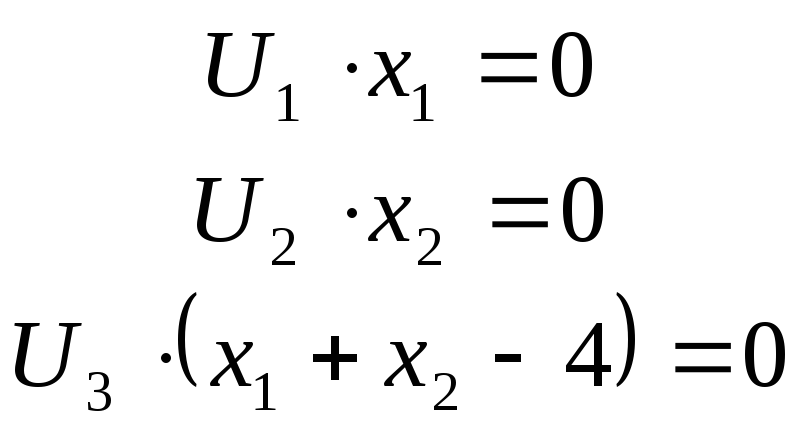
Следовательно, необходимо решить пять уравнений с пятью неизвестными. Три последних уравнения содержат произведение двух сомножителей, каждое из которых может быть равно 0, поэтому необходимо рассмотреть все возможные случаи (8 вариантов).

2.6. Оптимальное проектирование системы с распределенными параметрами

В различных технических задачах целью является выбор формы элемента конструкции. Типичными, например, являются задачи отыскания распределений толщин для силовых балок и пластин переменной формы. В этих случаях для определения формы проектируемого объекта требуется найти бесконечное число параметров. Следовательно, целью оптимизации является выбор функции формы, отвечающий оптимальному проекту элемента конструкции.

Ситуация, в которой определяется управляющая функция, во многом сходна с проблемами, возникающими в теории оптимального управления. Однако имеется существенное различие между вопросами оптимального проектирования механических систем и теорией оптимального управления, которое заключается в том, что в теории оптимального управления функция управления зависит от времени и ищется управляющий закон, гарантирующий оптимальное поведение системы в процессе ее работы. При оптимальном же проектировании механических систем управляющая функция зависит только от пространственных переменных и не изменяется в течение всего времени своего существования.

Второе важное отличие между оптимальным проектированием и управлением заключается в том, что в теории оптимального управления формулируются задачи с начальными условиями. При оптимальном же проектировании механических систем часто требуется решать задачи с граничными условиями и находить распределение деформаций и напряжений в упругом теле.

Следует отметить, что термин "распределенный параметр" трактуется для обозначения управляющей функции в одно-, двух- и трехмерном пространствах. При этом в случае одной изменяемой пространственной переменной исходная граничная задача описывается обыкновенными дифференциальными уравнениями. Задачи с двумя и тремя пространственными переменными включают уравнения с частными производными. В литературе же по оптимальному управлению исходную задачу рассматривают как задачу с распределенными параметрами только в случае уравнений с частными производными.