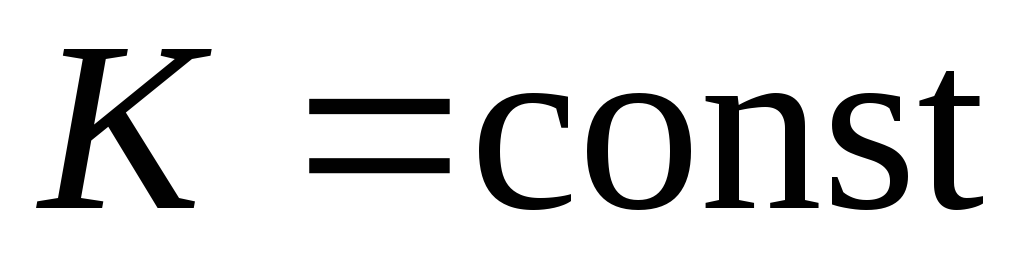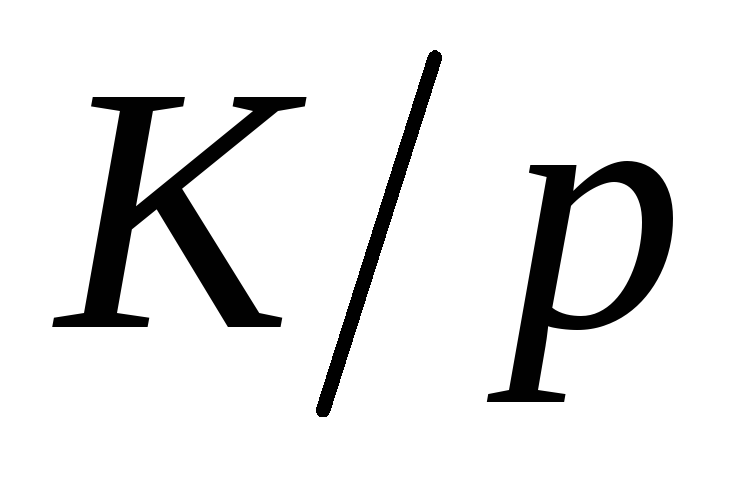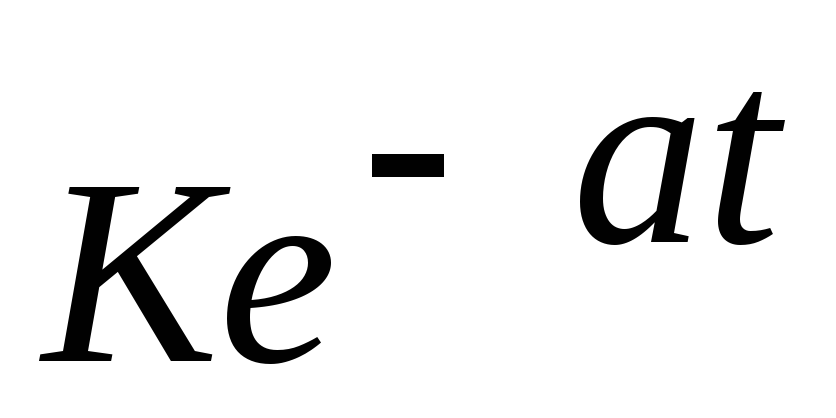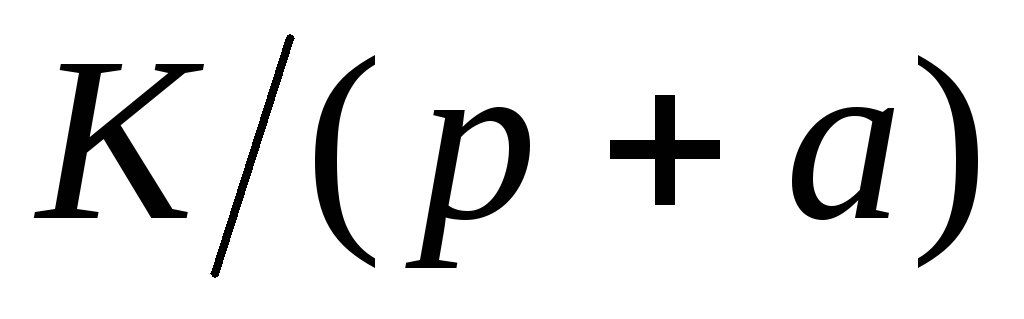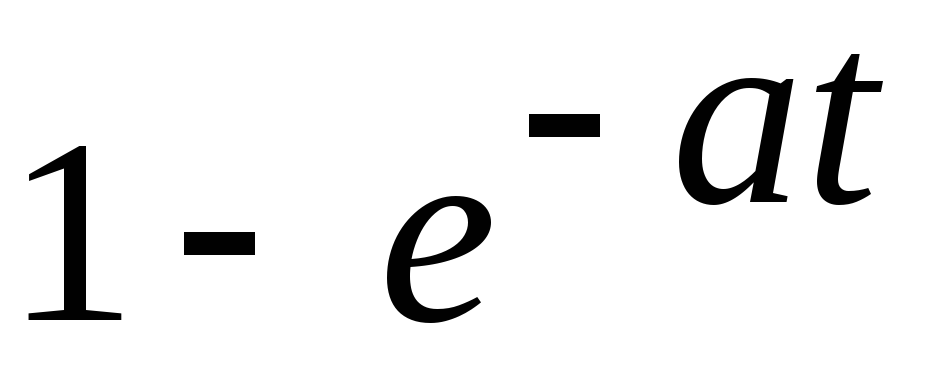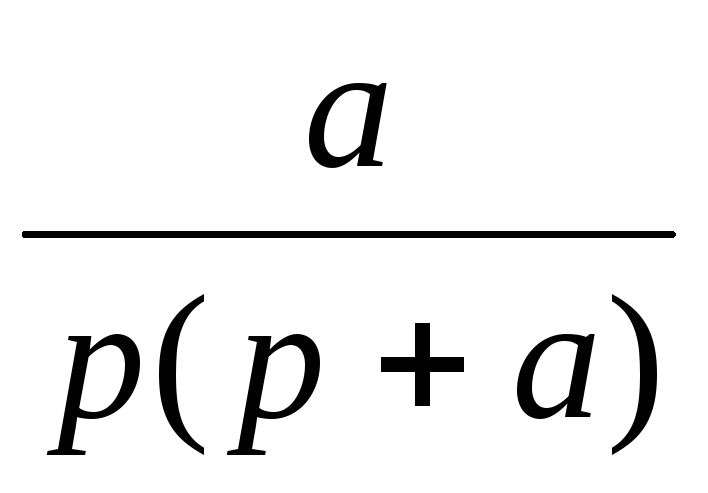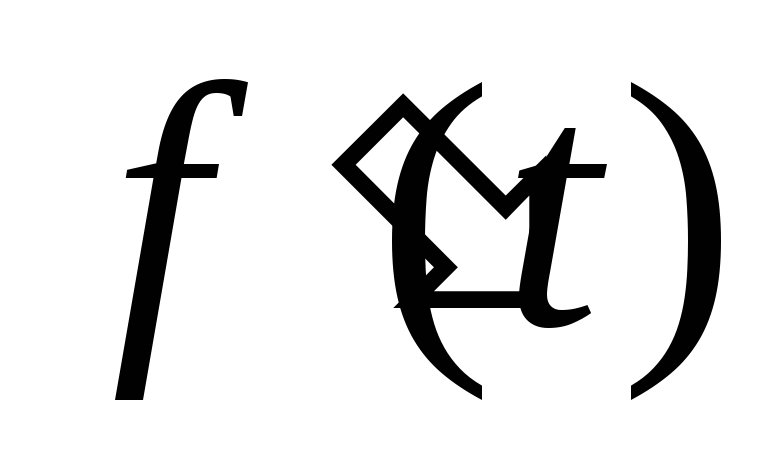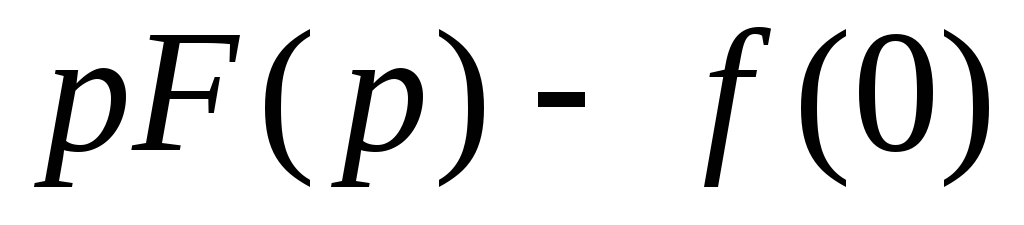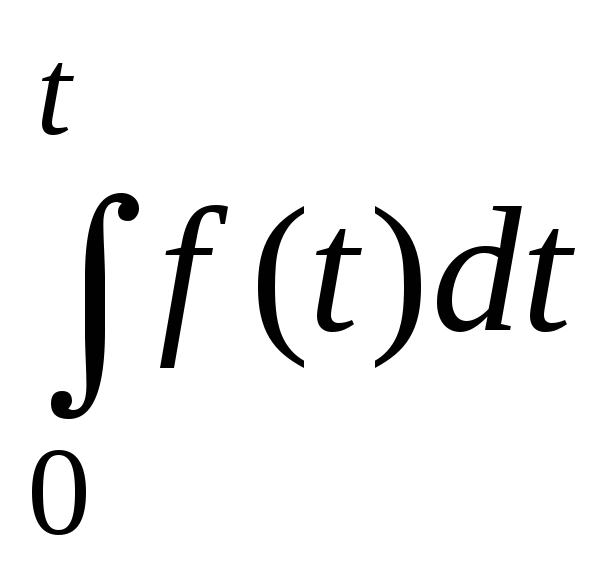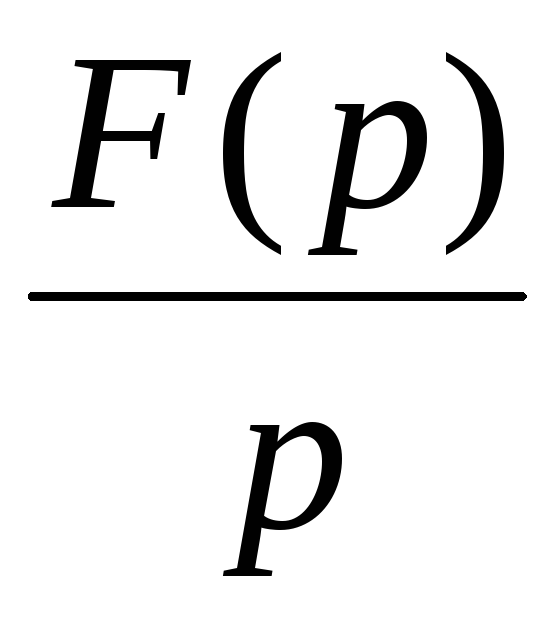6. 2. Применение интегрального преобразования Лапласа для расчета переходных процессов (операторный метод)
6.2.1. Основы операторного метода
Как известно, переходные процессы в линейных электрических цепях с постоянными параметрами описываются линейными дифференциальными уравнениями с постоянными коэффициентами. Решение таких уравнений можно выполнить с помощью интегрального преобразования Лапласа. Этот способ решения также называют операторным методом расчета. В данном методе действительные функции времени t, называемые оригиналами, т.е. функциями времени, заменяют их изображениями, т.е. функциями комплексной переменной р.
Преобразование
Лапласа выбрано потому, что оно заменяет
операции дифференцирования и интегрирования
функций времени простыми алгебраическими
операциями над их изображениями. Это
позволяет дифференциальные уравнения
для оригиналов перевести в алгебраические
уравнения для их изображений. Затем
полученные решения алгебраических
уравнений в виде операторных изображений
искомых токов и напряжений переводят
в область функции времени t,
т. е. находят оригиналы
Поскольку решение алгебраических уравнений, как правило, легче, чем решение дифференциальных уравнений, то преимущества операторного метода очевидны. Поэтому этот метод нашел широкое применение не только в электротехнике, но и в других областях науки.
6.2.2. Преобразование Лапласа
Преобразование
Лапласа представляет собой интегральное
уравнение, связывающее функцию
действительной переменной времени и
функцию
комплексной переменной р:
(6.12)
Это
уравнение называется прямым преобразованием
Лапласа, в котором L
является условным обозначением этого
преобразования,
называется оператором,
- оригиналом, а
- изображением.
Вместо
(6.12) соответствие между функциями
и
может записываться и так:
Для
того, чтобы можно было провести
преобразование (6.12), функция
при
>0
должна за любой конечный промежуток
времени иметь конечное число разрывов
первого рода и конечное число максимумов
и минимумов, а также иметь ограниченный
порядок возрастания. То есть для данной
функции
можно указать такие положительные числа
А
и a,
при которых
<
.
Поэтому при a< а = Re (р)
(6.13)
При
этих ограничениях интеграл (6.14) существует,
а значит можно найти операторное
изображение функции
.
Следует отметить, что для постоянных,
синусоидальных и для большинства других
видов используемых токов и напряжений
эти ограничения выполняются, т.е. для
их расчета в переходном процессе применим
операторный метод.
Оригинал
по известному изображению
может быть найден с помощью обратного
преобразования Лапласа:
(6.14)
где
- условное обозначение этого преобразования.
Следовательно, интегрирование функции времени соответствует в операторной форме делению изображения этой функции на оператор р. Изображение некоторых функций, наиболее часто встречающихся в задачах электротехники, приведены в табл. 6.1. Подробные таблицы соответствия оригиналов и изображений приведены в специальных справочниках.
Таблица 6.1
-
Оригинал f (t)
Изображение F(p)
