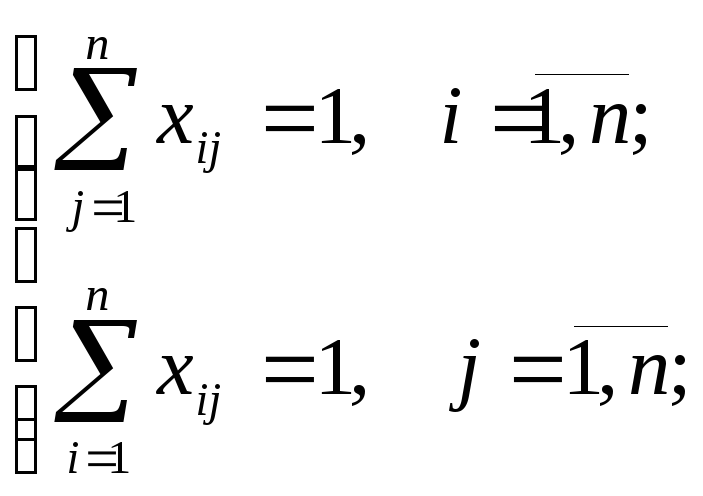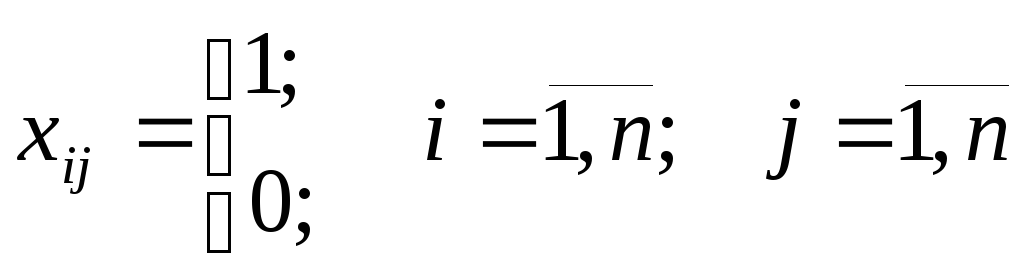4.1. Постановка задачи. Основные формулы

Пусть требуется выполнить n различных работ и имеется n работников для их выполнения, причем каждый работник может выполнить любой тип работ.

Цены производства разных работ для каждого работника может быть различной. Обозначим через  матрицу тарифов размером n на n. Элементы матрицывеличина заработной платы i-го работника на j-й работе. Пусть каждый работник может выполнять одновременно только одну какую-либо работу. Задача заключается в таком распределении работников по работам, при котором суммарная производительность максимальна.

Построим математическую модель этой задачи. Сопоставим каждому из возможных вариантов распределения работников по работам набор значений неизвестных , относительно которых условимся, что, если в данном варианте i-й работник назначается на j-ю работу, и , если i-й работник назначается не на j-ю работу. Для любого варианта среди чисел должно быть точно n единиц, причем должны выполняться следующие условия: (каждый работник назначается на одну работу) и (на каждую работу назначается один работник).

Суммарная стоимость при данном варианте назначения работников на работы выразится суммой: .

Таким образом, математическая модель задачи о назначениях будет такой:

	(4.1)
	(4.2)
	(4.3)

Задача о назначениях является частным случаем транспортной задачи. Существенным отличием является то, что искомые неизвестные являются двоичными или бинарными, поскольку принимают два значения ноль или единица.

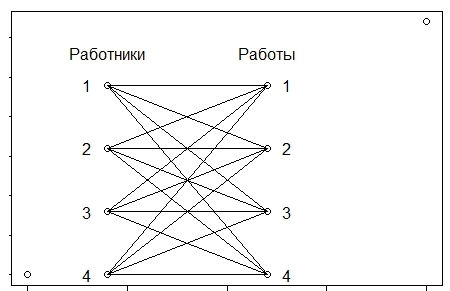
Эта задача имеет простую геометрическую интерпретацию, показанную на рис.(4.1). На нем изображен граф, у которого вершины слева обозначают работников, а вершины справа изображают работы. Вершины соединены ребрами с указанием их веса, при этом вес равен стоимости соответствующей работы.

Двудольный граф– граф, у которого существует такое разбиение множества вершин на две части (доли), что концы каждого ребра принадлежат разным долям. В нашей задаче тоже есть четкое разделение: одни вершины – это работники, другие – работы, а ребра соединяют только работников и работы.

Паросочетаниемнеориентированного графа G называется подмножество M его ребер E, выбранное так, что никакие два ребра из M не являются смежными, т.е. не имеют общей вершины. В терминах нашей задачи синонимом этому будет «назначение», чтобы каждый задействованный работник взял на себя отдельную работу. И не получилось такого, что два работника выполняет одну работу, или один работник отвечал за две работы.

Рис.4.1

Она является частным случаем задачи нахождения совершенного паросочетания (см.приложение).

Решение этой задачи может быть получено венгерским методом. Алгоритм был разработан и опубликован Гарольдом Куном (Harold Kuhn) в 1955 г. Сам Кун дал алгоритму название "венгерский", потому что он был в значительной степени основан на более ранних работах двух венгерских математиков: Денеша Кёнига (Dénes Kőnig) и Эйгена Эгервари (Jenő Egerváry). Основную суть метода рассмотрим на примере.

Пример

В цехе предприятия имеются четыре универсальных станка С1, С2, С3 и С4,, которые могут выполнять 4 вида работ: Р1, Р2, Р3 и Р4. Каждую работу единовременно может выполнять только один станок, и каждый станок можно загружать только одной работой.

В таблице 4.1 даны затраты времени при выполнении станком определённой работы. Определить наиболее рациональное распределение работ между станками, минимизирующее суммарные затраты времени.

Таблица 4.1

Затраты времени на выполнение работ

Станки	Работы
	1	2	3	4
1	68	72	75	83
2	56	60	58	63
3	38	40	35	45
4	47	42	40	45

Решение:

Решение сводится к последовательному преобразованию матрицы затрат, при этом у каждой следующей матрицы оптимальное распределение работ будет такое же, как и у исходной.

Суть метода основана на простой идее, которая состоит в том, что если равно нулю, то i-го работника целесообразно назначить на j-ю работу. Очевидно, что такое назначение будет не хуже любого другого. Если в матрице достаточно много нулей, то каждому работнику можно назначить работу с нулевой ценой, суммарная стоимость всех работ будет также равна нулю. Будем поэтапно строить такую матрицу. На каждом этапе, используя свойства двудольного графа, связанного с матрицей, будет построена новая матрица, которая будет, в некотором смысле, лучше предыдущей, поскольку будет содержать больше нулей.

Алгоритм венгерского метода.

Обозначим через XиYмножество работников и работ соответственно, через m– номер шага в алгоритме.

1. Преобразуем исходную матрицу , таким образом, чтобы в каждой строке и каждом столбце был нулевой элемент. Получим матрицу. После этого шага будем полагать, чтоm=1.

2. Используя , строим двудольный граф, для которого строим наибольшее паросочетание.

3. Если это паросочетание является совершенным, то искомое назначение найдено.

4. Если это паросочетание не является совершенным, строим множество вершин X_mиY_m изXиY, не входящих в паросочетание.

5. Строим новую матрицу 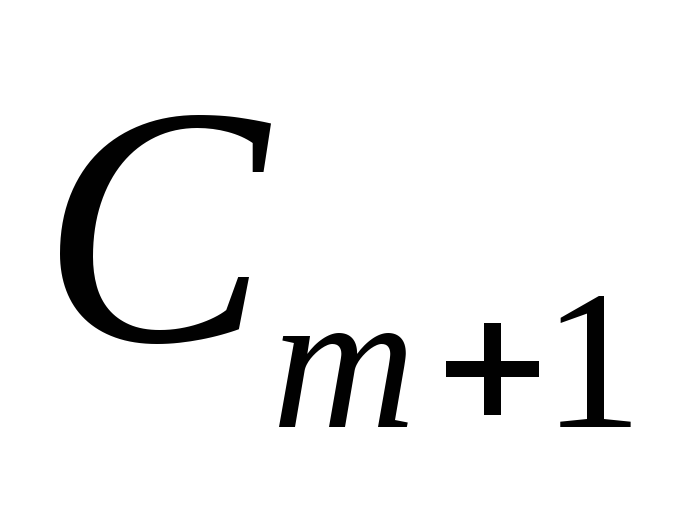, используя значенияX_mиY_m . Увеличиваемmна единицу и переходим к п.2.

Реализуем указанный алгоритм на рассматриваемом примере

Преобразование исходной матрицы , в соответствии с п.1 приведено на рис. 4.2. Сначала найдем минимальный элемент в каждой строки и вычтем его из элементов соответствующей строки. Преобразованная матрица расположена в интервале А10:Е14. В результате такого преобразования каждая строка содержит, по крайней мере, один нулевой элемент. Найдем минимальный элемент в каждом столбце и вычтем его из элементов соответствующего столбца. Преобразованную матрицу обозначим, она расположена в интервале Н10:К14. В результате такого преобразования каждый столбец и каждая строка матрицысодержит, по крайней мере, один нулевой элемент.

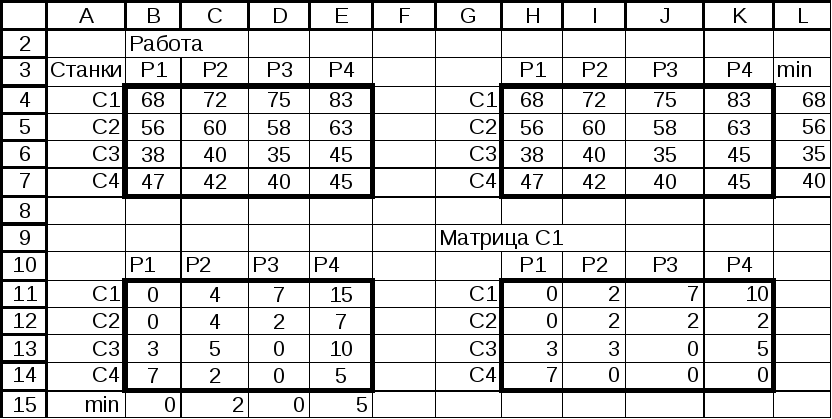
Рис.4.2

Выполним п.2 алгоритма. Для этого сопоставим матрице двудольный граф, у которого ребра определяются нулевыми элементами (рис.4.3.а). Сопоставим этому двудольному графу паросочетание, изображенное на рис.4.3.бтолстыми ребрами. Это сочетание является максимальным, но не является наибольшим.

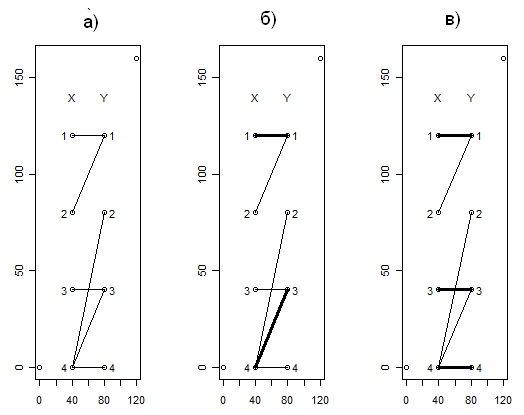Рис.4.3

Введем в рассмотрение понятие чередующейся цепи.

Чередующаяся цепь состоит из нечетного числа чередующихся тонких (из XвY) и толстых (в обратном направлении) ребер, начиная и кончая тонким ребром. Если такая цепь существует, то число ребер в паросочетании можно увеличить, поменяв толстые и тонкие ребра в этой цепи. В противоположном случае (если нет чередующейся цепи) данное паросочетание является наибольшим.

Заметим, что цепь на рис.4.3.бопределяемая последовательностью вершин {x₃, y₃,x₄, y₄} является чередующейся. Ребра, соединяющие вершиныx₃и y₃ , а такжеx₄и y₄ – тонкие, а реброy₃иx₄ – толстое. Поменяем тонкие и толстые ребра в цепи. Получим граф, показанный на рис. 4.3.в, в котором нет чередующейся цепи, поэтому данное паросочетание является наибольшим. Поскольку число толстых ребер равно 3, что меньше числа работников (равно 4), то паросочетание не является совершенным. Переходим к выполнению п.4.

Выделим множества вершин, не входящие в паросочетание. Это X_m= {x₂},Y_m= {y₂}. Составим множества вершин, которые входят в цепи, соединяющиеX_mиX(при этом отXкYможно двигаться по тонким ребрам, в обратном направлении — по толстым.

P_m= {x₂,x₁},Q_m= { y₁}.

Переходим к выполнению п.5. Преобразуем матрицу . Будем рассматривать строки с номерами элементов множестваP_mи столбцы с номерами элементов множестваY \ Q_m (столбцы которые не входят вQ_m), т.е. в матрице, которая получается путем удаления указанных строк и столбцов (на рис.4.4 удаляемые элементы заштрихованы). Найдем минимальный элемент в не заштрихованной части, он равен двум.

Рис.4.4.

Продолжим преобразование матрицы (рис.4.5). Из всех элементов первых двух строк вычтем найденный минимальный элемент, равный 2 , получим промежуточную матрицу, которая расположена в интервале А25:Е29. Прибавим это же значение равное двум ко всем элементам первого столбца матрицы. Получим матрицу, которая расположена в интервале Н10:К14.

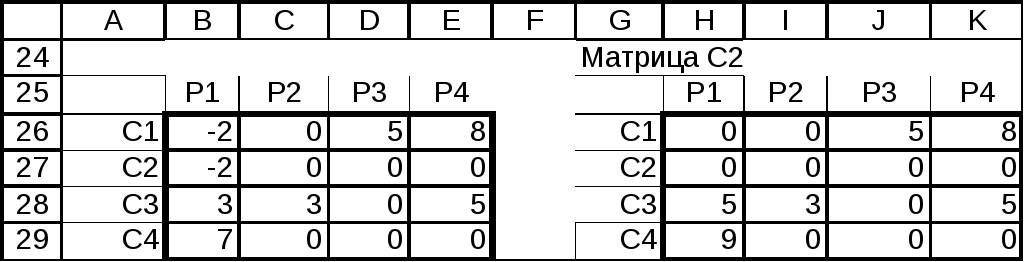
Рис.4.5.

Переходим к п.2. Матрице соответствует свой двухдольный граф, показанный на рис.4.6.а. Для этого графа можно построить паросочетание рис.4.6.б. Поскольку число толстых ребер равно 4, что равно числу станков и работ (равны 4), то паросочетание является совершенным. Т.о. этому совершенному соответствует оптимальное назначение.

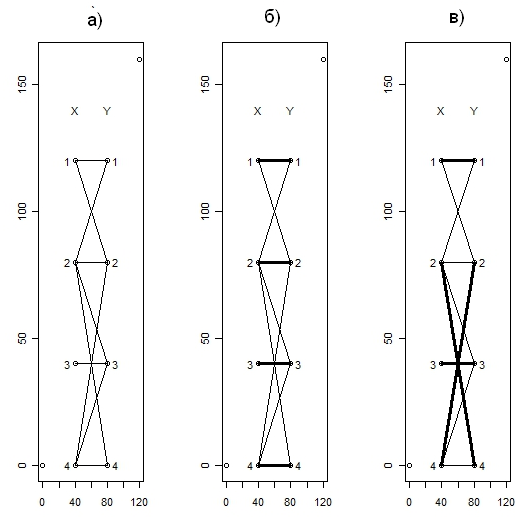
Рис.4.6

В соответствии с этим паросочетанием, первую работу x₁ следует выполнять на первом станкеy₁, стоимость этой работы 68;

работу x₂ - на станкеy₂, стоимость - 60 ;

работу x₃ - на станкеy₃, стоимость - 35;

работу x₄ - на станкеy₄, стоимость - 45.

Суммарная стоимость выполненных работ равна 208.

Заметим, что указанное паросочетание является не единственным совершенным. Другое совершенное паросочетание показано на рис.4.6.в., а суммарная стоимость выполненных работ также равна 208.

Решим данную задачу в MS Excel, используя надстройку«Поиск решения». Схема решения этой задачи совпадает с общей схемой решения транспортной задачи линейного программирования, которая была рассмотрена ранее.

Заполним лист MS Excel, как показано на рисунке 4.7. На рис. 4.8. показан тот же лист в режиме отображения формул. Диалоговое окно надстройки «Поиск решения» было заполнено с учетом специфики задачи – искомые переменные являются двоичными переменными (рис.4.8).

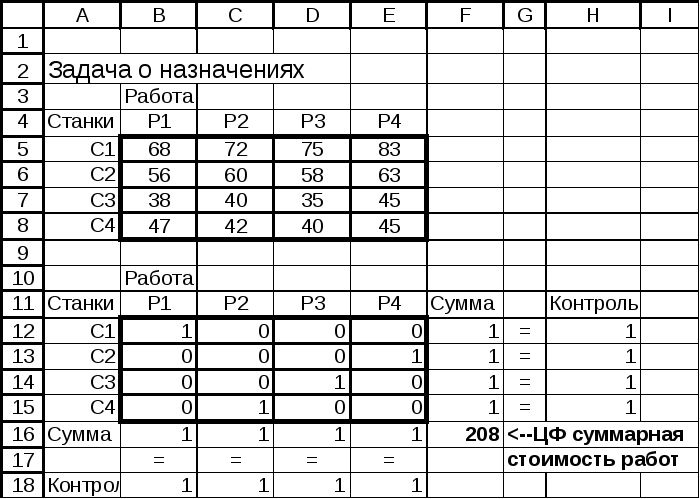
Рис.4.7.

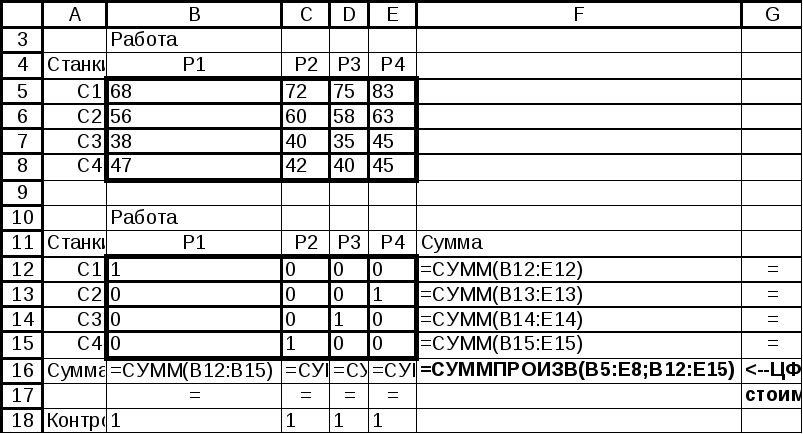
Рис.4.8.

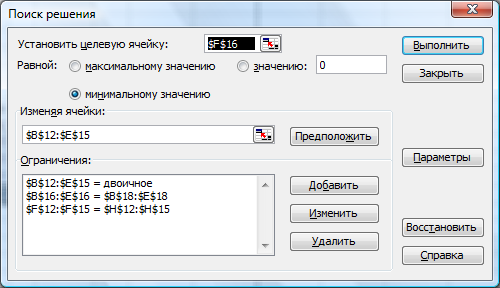
Рис.4.9.

Полученное решение приведено на рис.4.7

В соответствии с этим решением, первую работу x₁ следует выполнять на первом станкеy₁, стоимость этой работы 68;

работу x₂ - на станкеy₄, стоимость - 63;

работу x₃ - на станкеy₃, стоимость - 35;

работу x₄ - на станкеy₂, стоимость - 42.

Суммарная стоимость выполненных работ равна 208.

Полученное назначение соответствует графу, приведенному на рис.4.6.в.