Расчётные формулы.

Часто при анализе эмпирических данных возникает необходимость найти функциональную зависимость между величинами x и y, которые получены в результате опыта или измерений.

Х_i (независимая величина) задается экспериментатором, а y_i , называемая эмпирическими или опытными значениями получается в результате опыта.

Аналитический вид функциональной зависимости, существующей между величинами x и y обычно неизвестен, поэтому возникает практически важная задача - найти эмпирическую формулу

, (1)

(где - параметры), значения которой привозможно мало отличались бы от опытных значений.

Согласно методу наименьших квадратов наилучшими коэффициентами считаются те, для которых сумма квадратов отклонений найденной эмпирической функции от заданных значений функции

(2)

будет минимальной.

Используя необходимое условие экстремума функции нескольких переменных – равенство нулю частных производных, находят набор коэффициентов , которые доставляют минимум функции, определяемой формулой (2) и получают нормальную систему для определения коэффициентов:

(3)

Таким образом, нахождение коэффициентов сводится к решению системы (3).

Вид системы (3) зависит от того, из какого класса эмпирических формул мы ищем зависимость (1). В случае линейной зависимости система (3) примет вид:

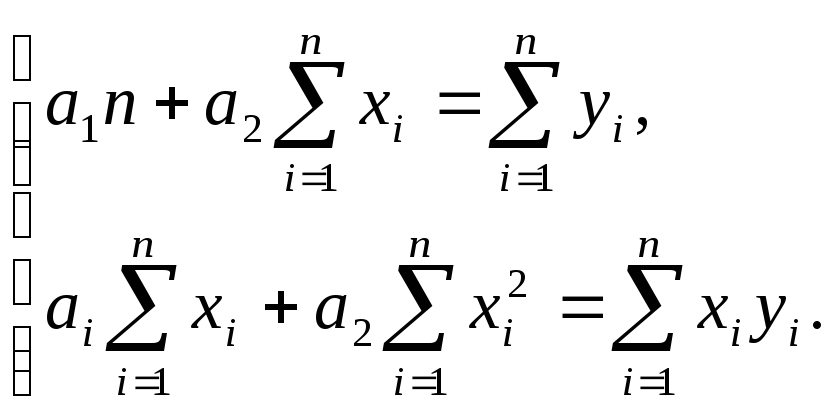
(4)

В случае квадратичной зависимости система (3) примет вид:

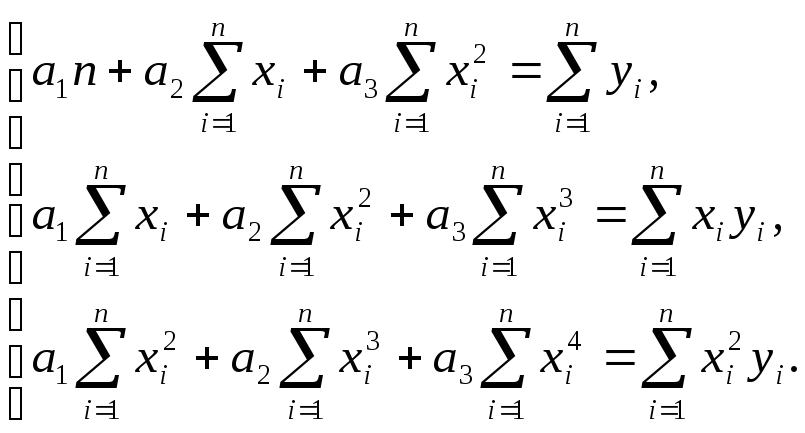(5)

В ряде случаев в качестве эмпирической формулы берут функцию в которую неопределенные коэффициенты входят не линейно. При этом иногда задачу удается линеаризовать т.е. свести к линейной. К числу таких зависимостей относится экспоненциальная зависимость

(6) где a₁и a₂ неопределенные коэффициенты.

Линеаризация достигается путем логарифмирования равенства (6), после чего получаем соотношение

(7)

Обозначим исоответственно черези, тогда зависимость (6) может быть записана в виде, что позволяет применить формулы (4) с заменойa₁ на ина.

График восстановленной функциональной зависимости y(x) по результатам измерений (xi, yi), i=1,2,…,n называется кривой регрессии. Для проверки согласия построенной кривой регрессии с результатами эксперимента обычно вводят следующие числовые характеристики: коэффициент корреляции (линейная зависимость), корреляционное отношение и коэффициент детерминированности.

Коэффициент корреляции вычисляется по формуле:

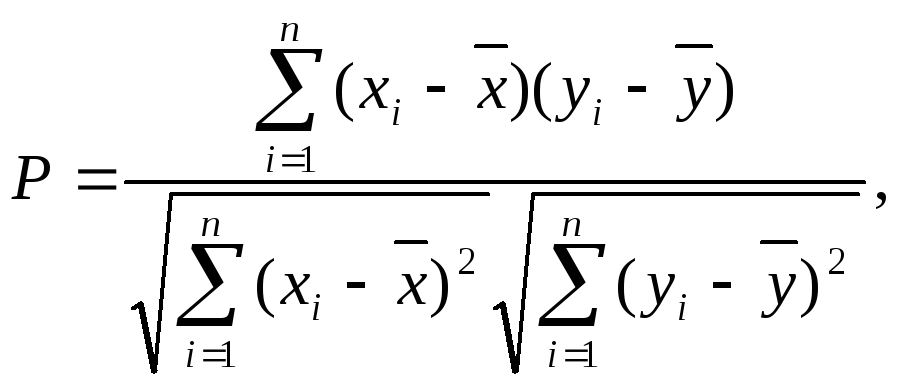(8)

где - среднее арифметическое значение соответственно поx, y.

Коэффициент корреляции между случайными величинами по абсолютной величине не превосходит 1. Чем ближе к 1, тем теснее линейная связь междуx и y.

В случае нелинейной корреляционной связи условные средние значения располагаются около кривой линии. В этом случае в качестве характеристики силы связи рекомендуется использовать корреляционное отношение, интерпретация которого не зависит от вида исследуемой зависимости.

Корреляционное отношение вычисляется по формуле:

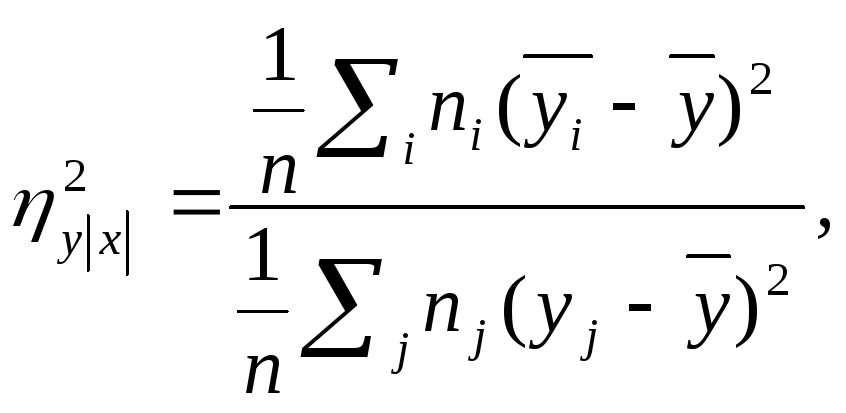(9)

где а числитель характеризует рассеяние условных средних околобезусловного среднего.

Всегда. Равенство= соответствует случайным некоррелированным величинам;= тогда и только тогда, когда имеется точная функциональная связь между x и y. В случае линейной зависимости y от x корреляционное отношение совпадает с квадратом коэффициента корреляции. Величина используется в качестве индикатора отклонения регрессии от линейной.

Коэффициент детерминированности определяется по формуле:

(10)

где S_{ост =} - остаточная сумма квадратов, характеризующая отклонение экспериментальных данных от теоретических.

S_полн - полная сумма квадратов, гдесреднее значениеy_i.

- регрессионная сумма квадратов, характеризующая разброс данных.

Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента детерминированности r², который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными. Если он равен 1, то имеет место полная корреляция с моделью, т.е. нет различия между фактическим и оценочным значениями y. В противоположном случае, если коэффициент детерминированности равен 0, то уравнение регрессии неудачно для предсказания значений y.

Коэффициент детерминированности служит показателем тесноты связи между независимой переменной и предиктом. Иногда показателям тесноты связи можно дать качественную оценку (шкала Чеддока):

Количественная мера тесноты связи	Качественная характеристика силы связи
0,1-0,3	Слабая
0,3-0,5	Умеренная
0,5-0,7	Заметная
0,7-0,9	Высокая
0,9-0,99	Весьма высокая

Любая сумма квадратов отклонений связана с числом степеней свободы (df- degrees of freedom), т.е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант. Поскольку при заданном объеме наблюдений по X и Y регрессионная сумма квадратов при линейной регрессии составляет n-2. Число степеней свободы для общей суммы квадратов определяется числом единиц, и поскольку мы используем среднюю вычисленную по данным выборки, то теряем одну степень свободы, т.е.

Итак, имеем два равенства:

(11)

Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений, или, что то же самое, дисперсию на одну степень свободы D.

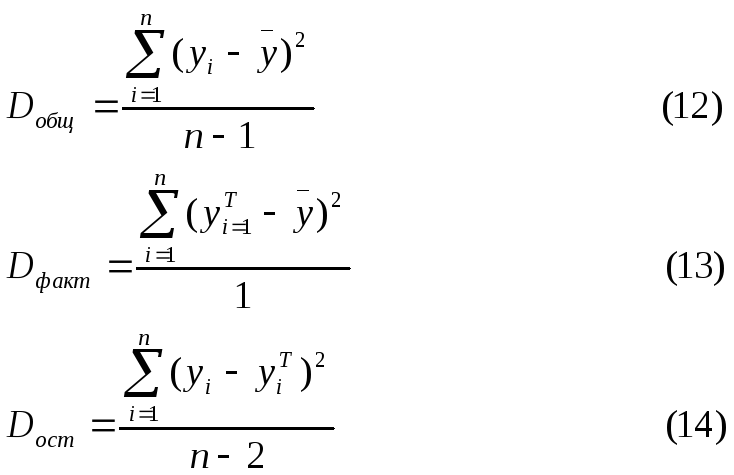
Определение дисперсии на одну степень свободы приводит дисперсии к справедливому виду. Сопоставляя регрессионную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-отношения (F-критерий):

где F – критерий для проверки нулевой гипотезы H0:

Если нулевая гипотеза справедлива, то регрессионная и остаточная дисперсии не отличаются друг от друга. Для H0 необходимое опровержение, чтобы регрессионная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F- отношения признается достоверным, если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: Fфакт >Fтабл. H0 отклоняется.

Если же величина окажется меньше табличной Fфакт <Fтабл , то вероятность нулевой гипотезы выше заданного уровня (например 0,05) и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статически незначимым. H0 не отклоняется.

Для проверки существенности в целом уравнения нелинейной регрессии по F – критерию Фишера F вычисляют через коэффициент детерминированности по формуле:

где - коэффициент детерминированности;n- число наблюдений; m – число параметров при переменных Х.

Величина m характеризует число степеней свободы для факторной суммы квадратов, а (n-m-1) – число степеней свободы для остаточной суммы квадратов.

Для линейной и экспоненциальной функций формула F – критерия примет вид:

Для параболы формула F – критерия примет вид :

В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка sa₁ и sa₂.

Стандартная ошибка коэффициентов регрессии a₂ определяется по формуле

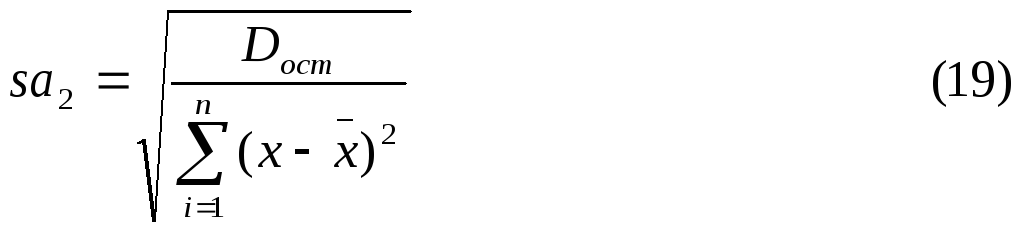
Величина стандартной ошибки совместно с t- распределением Стьюдента при n-2 степенях свободы применяется для проверки существенности коэффициента регрессии a₂ и для расчета его доверительных интервалов.

Для оценки существенности коэффициента регрессии a₂ его величина сравняется с его стандартной ошибкой, т.е. определяется фактическое значение t – критерия Стьюдента:

,

которая затем сравнивается с табличным значением при определенном уровне значимости a и числе степеней свободы n-2.

Стандартная ошибка параметра а₁ определяется по формуле:

Процедура оценивания существенности данного параметра не отличается от рассмотренного выше для коэффициента регрессии а₂;

Вычисляется t-критерий:

,

его величина сравнивается с табличным значением при df=n-2 степенях свободы.