Исследование динамических характеристик объекта управления по его математической модели

В результате линеаризации нелинейной модели объекта управления получено некоторое линейное дифференциальное уравнение 2 порядка. В частности, для варианта «Пример», линеаризованное уравнение имеет вид:

0,01Y + 0,091Y + Y = 0,258X, (14)

Напомним, что Y=и Y= - производные по времени, а (14) это уравнение в отклонениях от номинального (знак  опущен для простоты записи).

Для уравнения 2 порядка каноническая форма записи имеет вид:

T²Y + 2TY + Y = KX (15)

где Т – постоянная времени объекта, с; К – коэффициент усиления объекта по каналу X – Y;  - так называемый коэффициент демпфирования, смысл которого будет рассмотрен позже.

Следует отметить важность приведения к канонической форме для получения правильных значений параметров объекта. Характерна черта канонической формы дифференциального уравнения объекта - это то, что при выходной переменной (Y) коэффициент равен 1.

Сравнивая выражения (14) и (15), получим:

T = 0,102;  = 0,448; K=0,258.

Применим к уравнению (14) преобразование Лапласа.

Напомним, что для некоторой функции f(t) преобразование Лапласа определяется, как:

,

где р – комплексная переменная.

Для величин, входящих в уравнение (14), преобразование Лапласа имеет вид:

;

;

С учетом этого, уравнение (16) имеет следующий вид:

, или

(16)

Уравнение (16) называется изображением по Лапласу для уравнения (15). Полином, стоящий в левой части уравнения (16), носит название характеристического полинома.

Уравнение 0,08р² + 0,26р +1 =0 называется характеристическим уравнением.

Для анализа объекта управления обычно используют два вида типовых возмущения:

Х= 1[t] – единичный скачек

Х=[t] – мгновенный импульс

Решение Y(t) при X = 1[t] называется переходной характеристикой объекта управления h(t). Решение Y(t) при X = [t] называется импульсной характеристикой (функцией веса) объекта w(t).

Следует отметить, что весовая функция w(t) является производной от функции переходного процесса h(t).

Решение дифференциального уравнения ищется в виде суммы экспонент. Вид решения зависит от входного сигнала.

Для звена второго порядка эти решения имеют вид:

(17)

(18)

Здесь р₁; р₂ – корни характеристического уравнения, которые определяются, как ;С₁,С₂ – постоянные интегрирования, определяемые из начальных условий.

Следует обратить внимание на величину . В случае, когда >1, дискриминант положителен и корни р₁; р₂ получаются вещественными. Переходной процесс называется монотонным.

В случае, когда 0<=<1, дискриминант отрицательный и корни р₁; р₂ получаются комплексными, вида где. В этом случае, выражение (17) можно представить в виде:

(19),

а выражение (18) в виде:

(20).

Здесь  - степень затухания амплитуды (учитывает вещественную часть корней характеристического уравнения);  - круговая частота колебаний выходной переменной (учитывает мнимую часть корней характеристического уравнения); А – начальная амплитуда колебаний,  - фазовый сдвиг.

Переходной процесс, получающийся при решении такого вида, называется колебательным.

Значение постоянных можно найти по выражениям:

Для варианта «Пример» 0<<1 (=0448). Параметры переходного процесса будут: =4,389; =8,76; А=1,119; =1,106. Тогда по (19) и (21)

(22)

(23)

Для получения монотонного процесса прибавим к  единицу. Тогда при >1 (=1,448): р_1­= -9,798 , р₂= -24,448, а по (17) и (18) получаем:

(24)

(25)

По приведенным выражениям строим графические характеристики, изображенные на рис.5 и рис.6.

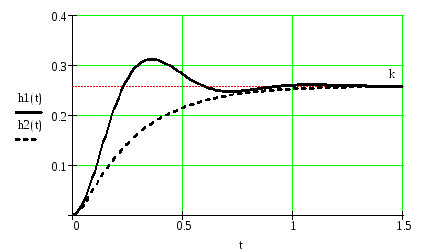
Рис. 3. Переходные характеристики объекта при >1 и 0<<1

Рис. 4. Импульсные характеристики объекта при >1 и 0<<1

Уравнение (16) можем переписать следующим образом:

(26)

Выражение вида при нулевых начальных условиях, называют передаточной функцией объекта управления.

В случае, когда к дифференциальному уравнению объекта управления применяют преобразование Фурье:

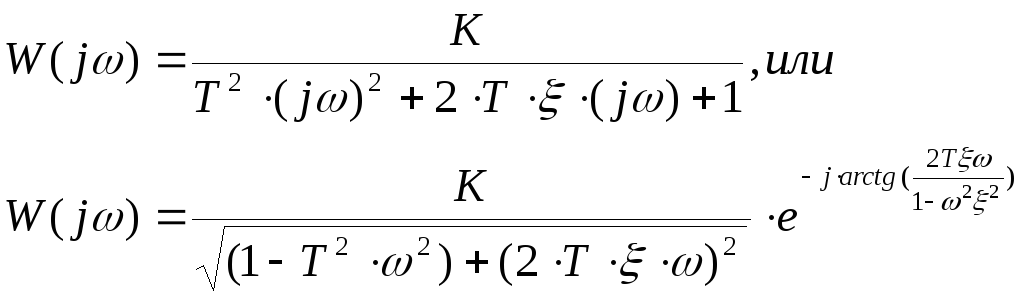(27)

Выражение (23) называют амплитудно-фазовой частотной характеристикой (АФЧХ) объекта управления, поскольку выражение, являющееся коэффициентом перед экспонентой, характеризует зависимость амплитуды колебаний, а показатель экспоненты – фазового сдвига от частоты.

АФЧХ можно разбить на две составляющие:

Амплитудно-частотную характеристику (АЧХ) – А()

Фазо-частотную характеристику (ФЧХ) - ()

АФЧХ объекта второго порядка имеет вид: , поэтому:

АЧХ: (28)

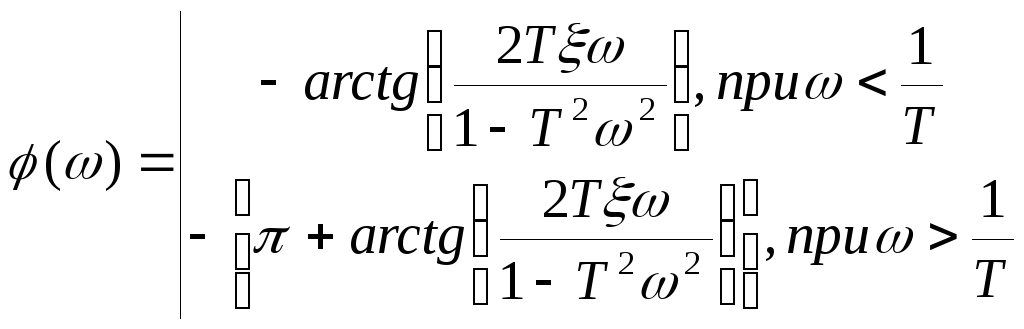ФЧХ: (29)

Следует отметить, что АФЧХ является комплексным числом, поэтому может быть представлена в виде:

Здесь Р() называется вещественной частотной характеристикой (ВЧХ), а Q() – мнимой частотной характеристикой (МЧХ), при этом:

;

Для рассматриваемого объекта АФЧХ имеет вид:

то есть:

; (30)

АФЧХ объекта строится в виде годографа на комплексной плоскости, при этом по оси абсцисс откладывают ВЧХ , а по оси ординат – МЧХ. Для варианта «Пример» получены графики, изображенные на рис. 5. Один для апериодического звена (=1,448>1), а другой для колебательного звена (0< =0,448 <1).

Рис. 5. Амплитудно-фазовая частотная характеристика

объекта управления

Выходят обаграфика из одной точки (K=0.258, i0), и приходят в начало координат, но форма их разная.

Фазо-частотная и амплитудно-частотная характеристики для =1,448>1 и 0< =0,448 <1, варианта "Пример", приведены на рис. 6 и рис.7.

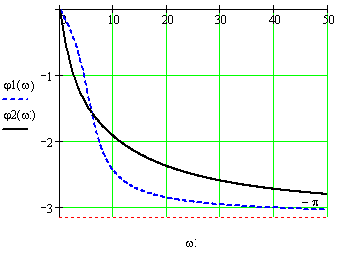
Рис. 6. Фазо-частотные характеристики

ФЧХ показывает зависимость фазового сдвига колебаний на выходе объекта управления относительно колебаний на его входе в зависимости от частоты колебаний входной величины. По частотным характеристикам объекта можно судить о многих параметрах системы управления, в частности, о ее устойчивости, что будет рассмотрено в следующей работе.

АЧХ показывает зависимость амплитуды колебаний выходной величины Y(t) от частоты изменения входной величины X(t). Для колебательного объекта (0<<1) частота, которой соответствует наибольшая амплитуда, является резонансной частотой.

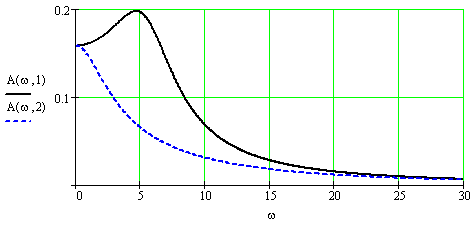
Рис.7Аамплитудно-частотные характеристики