Первичные изм. преобразователи. Часть 1

Наиболее распространенные уравнения пьезоэффекта

Таблица 4.2

Выбираемые величины

Дифференциалы

Уравнения

Термодинамические

Соотношение

Уравнение

Независимые

Функции

функций

для

функции

взаимосвязей

пьезоэффекта

определения

производных

δi

εj

dε

=

∂ε j

dδ

+

∂ε j

dE

дεj /дδi = SijE

H = V – D mEm - δiεj

εi = SijEδi +

j

∂δi

i

∂Em

m

дεi/дЕm=дDm/дδi=

dmiЕm

Еm

Dm

dDm

=

∂Dm

dδi

+

∂Dm

dEm

дDm

/дЕm

=

dH = - εjdδi – DmdЕm

dmi

Dm=εδmnEm+dni

∂δ

∂δ

ε

δ

δ

i

i

mn

i

εj

δi

dδi

=

∂δi

∂ε j +

∂δi

dEm

дδi

/ дεj

=

H2 = V – E mDm

δi = CijE εi +

E

emiЕm

∂ε j

∂Em

дδi /дЕ=дDm/дεi

Cij

ε

Еm

Dm

∂Dm

∂Dm

дDm

/дЕm

=

dH2 = δidεj – DmdЕm

150

= - emi

ε

dDm

=

∂ε j

∂ε j

+

∂Em

dEm

ε

Dn=ε mnEm+eni

ε mn

εi

δi

εj

dε j

=

∂ε j

∂δi +

∂ε j

dDm

дεj

/дδi = -

H1 = V – εjδi

εi = SijDδj +

SijD

gmiDn

∂δi

∂Dm

дεi/дDm =

D

Е

∂D

m

∂E

m

дЕ / дD =

dH = - ε dδ + Е dD

дЕm/дδi= - gmi

Em= βmnDn -

m

m

dEm

=

∂δi

+

dDm

δ m

m

1

j i m m

∂δi

∂Dm

β mn

gmj δj

εj

δi

dδi

=

∂δi

dε j +

∂δi

dDm

дδi

/ дεj

=

A= v

δi = CijD εi -

∂ε j

∂Dm

D

дδi/дDm = дЕm/дεi

hnjDn

Cij

= - hmi

Dm

Еm

∂Em

∂Em

дЕm / дDm =

dA = δidεj + DmdЕm

ε

dEm

=

∂ε j

dε j

+

dDm

ε

Em= β mnDn-

∂Dm

β mn

hmi εi

εj

δi

dδ

=

∂δi

∂ε

+

∂δi

dB

дδi

/ дεj

=

dv= δidεj + HmdBm

δi = Cijβεi -

j

∂ε j

j

∂Bm

m

Cijβ

дδi/дBm=дHm/дεi

£njBn

Bm

Hm

dH m =

∂H m

dε j

+

∂H m

dBm

дHm

/дBm

=

= - £mi

Hm= 1/µSmn Bn

∂ε j

∂Bm

S

- £mi εi

1/µ mn

Из певого уравнения системы можно записать

δ xx = C E .	(4.4.45)
ε xx
11

Подставим (4.4.44) и (4.4.45) в первое уравнение системы (4.4.43)

δ xx		=	C11E + e112	= C D .	(4.4.46)
			ε ε
ε				11
	xx	11

Отсюда CD11>CE11, т.е. модуль упругости измерений при постоянном поле, меньше, чем модуль упругости, измеренный при постоянной индукции.

Теперь допустим, что δxx = 0. Из уравнения (4.4.43) находим

ε		=	e2	E	x		(4.4.47)
	xx		11			.
			C E
				11

Подставим (4.4.47) во второе уравнение системы (4.4.43)

D			ε ε	+ e2	= ε δ .
	x	=	11	11
E			C E		11
	x
				11

Перепишем уравнения (4.4.46) и (4.4.48) следующим образом:

			1 + e2
C11D =			11			C11E	,
			C Eε ε
			11 11
	1 + e2
ε11δ	=		11		ε11ε .
			E δ
	C11ε11

(4.4.48)

(4.4.49)

Если систему (4.4.49) разрешить по отношению к множителю в скобках и приравнять левые части полученных уравнений, тогда

		C Dε ε					= C Eε δ .						(4.4.50)
			11	11					11	11
Обозначим выражение
	e2					e2				2
11							11
			=						= K11 .				(4.4.51)
	C Eε ε				C Eε δ
11		11				11		11
С учетом выражения (4.4.51) уравнение (4.4.49) перепишем в виде
			C D			= C E (1 + K 2					),
				11				11		11			(4.4.52)
			ε δ = ε ε (1 + K 2 ).									,
			11					11		11
								151

где К11 - коэффициент электромеханической связи. Первый индекс при коэффициент электромеханической связи указывает на направление распространения энергии, второй соответствует той деформации, при которой эта энергия накопилась.

И, наконец, для прямого пьезоэффекта можно записать:

Pxx = e11 εxx + e12 εyy + e13 εzz + e14 εyz + e15 εxz + e16 εxy,

Pyy = e21 εxx + e22 εyy + e23 εzz + e24 εyz + e25 εxz + e26 εxy,

(4.4.53)

Pzz = e31 εxx + e32 εyy + e33 εzz + e34 εyz + e35 εxz + e36 εx.;

Или в другой форме

- Pxx = d11 δxx + d12 δyy + d13 δzz + d14 δzy + d15 δzx + d16 δxy,

- Pyy = d21 δxx + d22 δyy + d23 δzz + d24 δzy + d25 δzx + d26 δxy,

(4.4.54)

- Pzz = d31 δxx + d32 δyy + d33 δzz + d34 δzy + d35 δzx + d26 δxy.

Подобным образом могут быть записаны для обратного пьезоэффекта:

-δxx = e11 Еx + e21 Еy + e31 Еz,

-δyy = e12 Еx + e22 Еy + e32 Еz,

-δzz = e13 Еx + e23 Еy + e33 Еz,

- δzy = e14 Еx + e24 Еy + e34 Еz,

(4.4.55)

-δzx = e15 Еx + e25 Еy + e35 Еz,

-δxy = e16 Еx + e26 Еy + e36 Еz.

Уравнения для деформации имеют вид

εxx = d11 Еx + d21 Еy + d31 Еz,

εyy = d12 Еx + d22 Еy + d32 Еz,

εzz = d13 Еx + d23 Еy + d33 Еz,

ε yz = d14 Еx + d24 Еy + d34 Еz,

(4.4.56)

εxz = d15 Еx + d25 Еy + d35 Еz,

εxy = d16 Еx + d26 Еy + d36 Еz.

152

Составим матрицу для пьезомодулей уравнения (4.4.55)

e11 e12 e13 e14 e15 e16,

e21 e22 e23 e24 e25 e26, ,

(4.4.57)

e31 e32 e33 e34 e35 e36.

где строки - это направление поля, столбцы - деформации. Пьезоэлектрические уравнения позволяют описать работу

преобразователей в режимах приема и излучения. Результаты приведенных исследований представляют интерес для изучения колебательных систем, имеющих форму различных геометрических тел таких как стержни, пластины, кольца.

4.5. Колебания стержня в электрическом поле, параллельном его толщине. Продольный пьезоэффект

Колебания, обусловленные деформацией растяжение-сжатие (продольные), имеют простую зависимость с постоянными кристалла. Рассмотрим пьезоэлектрический стержень (рис.4.5.1,а), толщина которого выбирается вдоль оси Х, длина - вдоль оси Z, ширина вдоль оси Y. Если на поверхности, перпендикулярной оси X нанести электроды, то единственной компонентой поля, отличной от нуля, будет Еx. При этом

Еy = Еz = 0,

(4.5.1)

поскольку к другим поверхностям электрическое напряжение не подводится. Электроды являются эквипотенциальными поверхностям, а поэтому в качестве электрических граничных условий примем постоянство поля Е. В свою очередь, эти граничные условия определяют выбор независимых переменных. В данном случае первой независимой переменной является Е.

Предположим, что длина стержня много больше, чем два других поперечных размера, а поэтому для плоской волны, распространяющейся вдоль оси X характерно постоянство деформаций. Тогда в качестве второй независимой переменной примем ε.

153

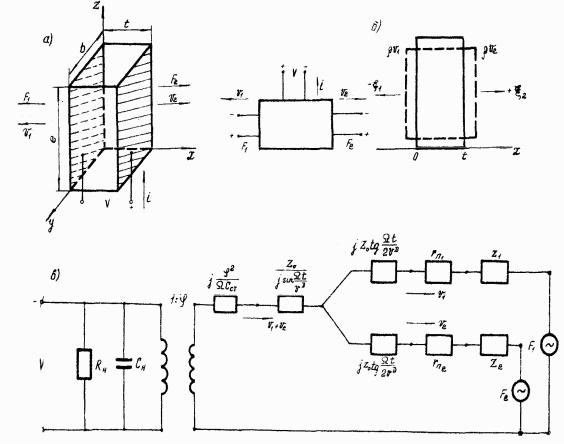
Рис.4.5.1. Схема стержня в электрическом поле, параллельном его

толщине:

а – к общей постановке задачи; б – с учетом граничных условий; в – электромеханическая схема

При указанных граничных условиях уравнения пьезоэффекта можно записать следующим образом:

E
δ xx = C11ε xx − e11Ex						,	(4.5.2)
D = ε ε			+ e ε
	E	x		xx	.
x 11			11

В стержне выделим элементарный объем с ребрами dx, dy, dz. Согласно закону Ньютона для такого объема можно составить уравнение движения:

ρdxdydz ∂2ξ = F ,

(4.5.3)

dt2 x

где ρ - плотность; ξ - смещение вдоль оси X; Fx - компоненты сил, действующих на элементарный объем вдоль оси X. Равнодействующая сил, действующих на элементарный объем, может быть получена из соотношений

154

F =	¶δ xx	+	¶δ yx	+	¶δ zx	.	(4.5.4)
x	¶x		¶y		¶z

В данном случае рассматривается элементарный объем, в котором волна распространяется вдоль оси Х. Тогда уравнение движения можно представить в виде

ρ × ¶2ξ = ¶δ xx . ¶t 2 ¶x

Продифференцируем уравнения (4.5.2) и получим

	¶δ xx		E ¶ε xx						¶Ex
			= C11				- e11				,
	¶x				¶x				¶x
	¶Dx			¶Ex				¶ε11
		= ε ε				+ e				.
	¶x				¶x			¶x
			11				11

Так как внутри элементарного объема dv D = 0, т.е.

∂Dx = 0 ,

¶x

то из уравнения (4.5.6) находим

∂Ex = - e11 × ∂ε xx .

¶x ε11ε ¶x

Подставим выражение (4.5.8) в первое уравнение системы (4.5.6):

(4.5.5)

(4.5.6)

(4.5.7)

(4.5.8)

¶δ xx

2

¶ε xx

¶ε xx

2

= C11E

¶ε xx

+

e11

×

=

C11E

+

e11

.

¶x

ε11ε

¶x ε11ε

¶x

¶x

Выражение в квадратных скобках обозначим как C11D и учтем, что

¶ε xx = ¶2ξ , ¶x ¶x2

(4.5.9)

(4.5.10)

так как ε xx	=	∂ξ . Тогда уравнение движения для рассматриваемого случая
		¶x
с учетом (4.5.5) и (4.5.9) запишется в виде
		¶2ξ	C D	¶2ξ
		¶t 2 =	11	× ¶x2 .	(4.5.11)
			ρ

Из уравнения (4.5.11) скорость продольной волны может быть определена как

155

V D =	C11D	.	(4.5.12)
	ρ

Решение уравнения (4.5.11) будем искать в виде стоячей волны:

ξ =

A sin

Ω

x + A cos

Ω

x

e jΩt ,

(4.5.13)

1

V

D

2

V

D

где

Ω

= K . Множитель

e jΩt

отбросим, так как нас интересуют только

V D

амплитудные значения переменных величин. Определим произвольные постоянные А1 и A2. Предположим, что стержень находится в среде и граничные условия можно представить в виде схемы, приведенной на рис. 4.5.1,б или следующим образом:

при х = 0

F1

ξ

х

=0

= −ξ ; δ

xx

x=0

= −V Z −

,

1

1 1

Scm

(4.5.14)

при х = t

,

ξ

= ξ

δ

= −V Z

−

F2

х

=t

;

xx

x=0

2

.

2

2

S

cm

где V1 = jΩ ξi –

колебательная

скорость;

Z1

= ρ1V1Scm; Z2 = ρ2V2Scm –

механическое сопротивление; Scm – площадь стержня.

Для определения произвольных коэффициентов из выражения (4.5.13) воспользуемся граничными условиями:

- ξ1 = A2

ξ2

= A1 sin

Ω

t − ξ1 cos

Ω

t .

(4.5.15)

D

D

V

V

Из второго уравнения (4.5.15) определим

ξ

+ ξ cos

Ω

t

A =

2

1

V D

.

(4.5.16)

sin

Ω

t

V D

Тогда общее решение уравнения движения примет вид

156

ξ

+ ξ cos

Ω

t

Ω

Ω

ξ =

2

1

V

D

sin

x − ξ1 cos

x .

(4.5.17)

sin

Ω

V D

V D

t

V D

Воспользуемся уравнениями для пьезоэффекта (4.5.2), с учетом граничных условий для напряжений (4.5.14)

- V1 Z1	- F1	= C E	εxx Scm – e 11Ex Scm,,
		11
- V2 Z2	– F 2	= C E	εxx Scm – e 11Ex Scm..	(4.5.18)
		11
Из уравнения (4.5.8)	определим Ex с учетом того, что F1			и F2 – силы

давления, созданные на поверхности стержня падающей на него акустической волной:

E

x

= −

e11

∫

∂ε xx

dx = −

e11ε xx

+ const .

(4.5.19)

ε ε

∂x

ε ε

11

11

t

Потенциал между

обкладками

стержня

−∫ Ex dx = V .

Таким образом,

0

можно определить постоянную интегрирования:

t

∂ξ − const dx = V .

−∫

e11

(4.5.20)

ε

0 ε11

∂x

Отсюда

−

e11

(ξ + ξ

2

) + t const = V .

(4.5.21)

ε ε

1

11

Тогда

const =

V

+

e11

(ξ + ξ

) .

ε ε t

2

t

1

11

(4.5.22)

Возвращаясь к уравнению (4.5.19) и подставляя значение произвольной постоянной, можно записать уравнение для напряженности электрического поля:

E

x x=0

= −

e11ε xx

+

V

+ e

ε ε t (ξ + ξ

) =

V

−

e11

ε

−1 t (ξ + ξ

)

.

(4.5.23)

ε

2

ε

xx

2

11

11 1

1

x=t

ε11

t

t ε11

157

Подставив (4.5.23)

V1Z1 - F1 = C11Eε xx Scm

			e2
	= Scmε xx C11E	+	11
			ε11ε

в (4.5.18), найдем

V

e

ε xx -1 t (ξ1

+ ξ2 )

- Scme11 ×

-

11

=

ε11ε

t

(4.5.24)

e S

e2

S

cm

(ξ1

+ ξ2 )

x=0 -

11

V -

11

cm

x=t .

ε

t

ε11t

Подставим уравнение (4.5.23) во второе уравнение (4.5.18) и получим

-V Z

2

- F = C Eε

S

cm

- S

cm

e E

x

=

2

2

11 xx

11

e2

e S

e2

S

(4.5.25)

= ε xx Scm

C11E +

11

x=0 -

11

cm

V

-

11

cm

(ξ1

+ ξ2 )

x=t .

ε

ε

ε11

e2

t

ε11t

S

cm

= ϕ , тогда

Введем обозначение

11

t

e112 Scm2 t

=

t

×

e112 Scm2

= ϕ 2C ,

ε

ε S

ε ε S

t

t2

cm

11

cm

11

cm

=

ε ε S

cm

(стержня) при

где

C

11

–

емкость

плоского

конденсатора

cm

t

отсутствии деформации. Так как смещение ξ =

V1

; ξ

=

V2

и

jW

jW

1

2

2

C11E +

e11

= C11D , то уравнение (4.5.24) может быть переписано в виде

ε11ε

-V1Z1 - F1 = C11Dε xx Scm

-ϕV -

ϕ

2

V1

+

V2

.

Ccm

jW

jW

Или

ϕ

2

C11D Scmε xx

x=0 + j

(V1 +V2 ) + V1Z1 + F1

= ϕV ,

CcmW

(4.5.26)

ϕ 2

D

C11 Scmε xx

x=t + j

(V1 + V2 ) +V2Z2 + F2

=

ϕV .

CcmW

Из уравнения (4.5.17) определим

ξ + ξ

cos

W

t

¶ξ

W

2

W

W

=

1

V

D

+ ξ1 sin

cos

x

x

.

W

¶x V D

V D

V D

sin V D t

158

Отсюда

Ω

ξ

2

Ω

ε

=

+ ξ ctg

t =

xx

x=0

D

Ω

D

V

1

V

sin V D t

ξ

+ ξ ctg

Ω

t sin

Ω

t + ξ

− ξ

Ω

2

1

V

D

V

D

1

1

=

=

(4.5.27)

V

D

Ω

sin V D t

V + V

Ω

=

1

+

1

2

jV tg

t

,

D

Ω

D

V

1

2V

sin V D t

где VD– скорость распространения волны. Аналогичным образом можно получить

ε

= −

1

V + V

− jV tg

Ω

(4.5.28)

j

1

2

t .

xx

x=t

D

Ω

D

V

1

2V

sin V D t

Если учесть, что Z0 = VDβScm, то из первого выражения системы (4.5.26)

можно получить

Z

0

ϕ 2

Ω

(4.5.29)

− j

Ω

(V1

+ V2 ) + j ΩCcm (V1 + V2 ) + jV1Z0tg 2V D t + V1Z1 + F1 =

ϕV

sin V D t

Из второго уравнения (4.5.26) с учетом (4.5.28) имеем

− j

Z

(V + V

) + j

ϕ 2

(V + V

) + jV Z

tg

D

t + V Z

+ F = ϕV (4.5.30)

Ω

ΩCcm

1

2

1

2

2 0

2V D

2

2

2

sin V D t

Ток, протекающий через стержень, определяется из уравнения

i = j Ω ScmDx

(4.5.31)

или

i = j Ω СcmV + φ(V1 + V2).

(4.5.32)

Уравнения (4.5.29), (4.5.30) и (4.5.32) позволяют построить

электромеханическую схему стержня (рис.4.5.1,в).

159