Лабораторная работа № 3 «Решение уравнений и систем»

Цель работы:С помощью средствMathCadнаучиться находить графическое, аналитическое, численное решения уравнений. Исследовать на разрешимость системы уравнений.

Рекомендуемая литература: [1-5, 10].

Задание:

1. Найти все корни уравнения n-ой степени: графически, численно и аналитически.

2. Сделать проверку полученного решения.

3. Найти численное и графическое решение трансцендентного уравнения.

4. Сделать проверку полученного решения.

5. Исследовать систему уравнений на разрешимость. Построить график.

6. Решить систему уравнений.

7. Сделать проверку полученного решения.

Таблица № 3.1: Варианты для лабораторной работы «Решение уравнений и систем»

№ вар.	Уравнение второй степени	Трансцендентное уравнение
1	2	3
1	2x^2-5x-3=0	e^-x=cos(x)
2	3x^2-8x+5=0	x=tg(x)
3	5x^2+9x+4=0	sin^2(x)=e^2x
1	2	3
4	36x^2-12x+1=0
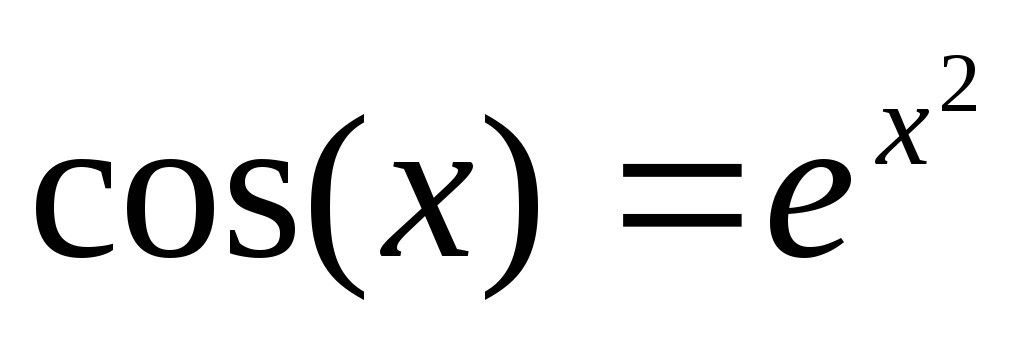
5	3x^2-3x+1=0	tg^2(x)-e^sin(x)=0
6	x^2+9x-22=0
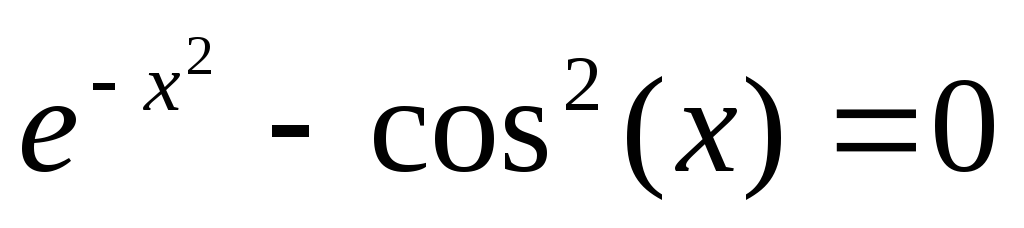
7	7x^2-11x-6=0	tg(x)-8ln(x)=0
8	x^2-12x+32=0
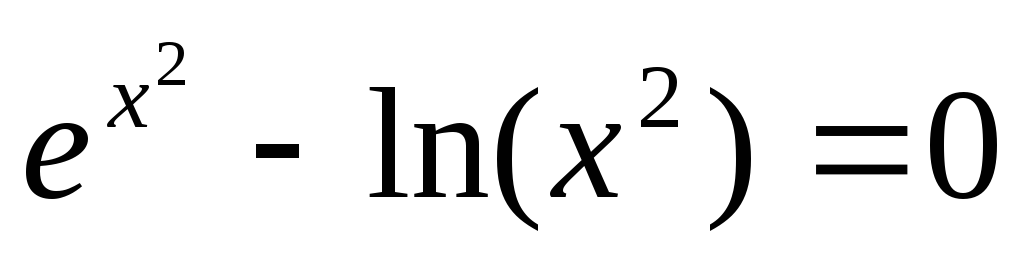
9	3x^2-10x+3=0	ln(x)=e^-x
10	x^2-8x-84=0
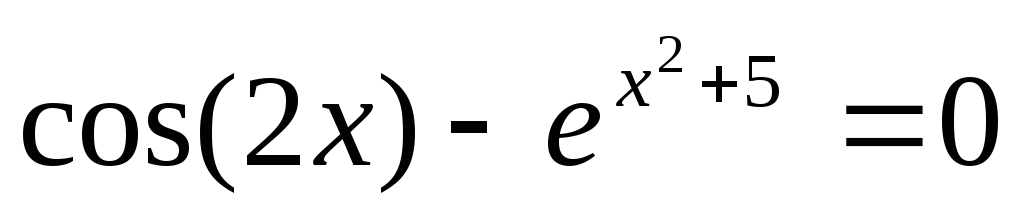
11	16x^2+8x+1=0
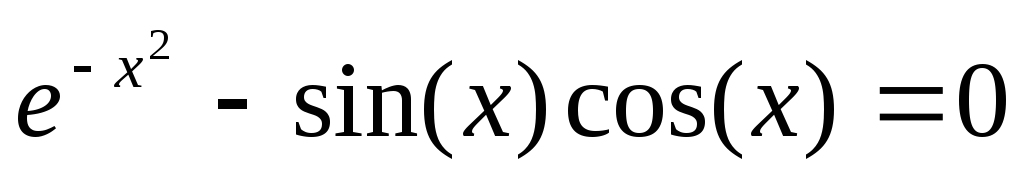
12	x^2+14x+33=0
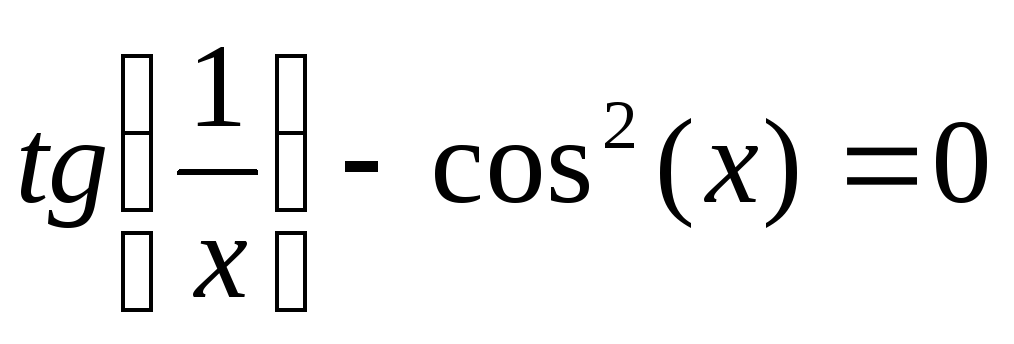
13	5x^2+26x-24=0	tg^2(x)-e^cos(x)=0
14	x^2-34x+289=0	x^2=cos(x)
15	10x^2-9x+2=0	x^3+1=tg(x)
16	x^2+48x+11=0	ln(x)=cos(2x)
17	7x^2-56x+20=0
18	4x^2+x-8=0
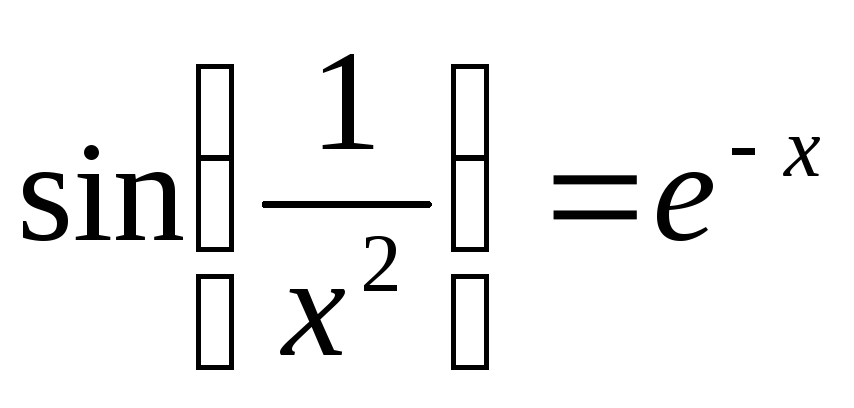
19	2x^2-5x+3=0
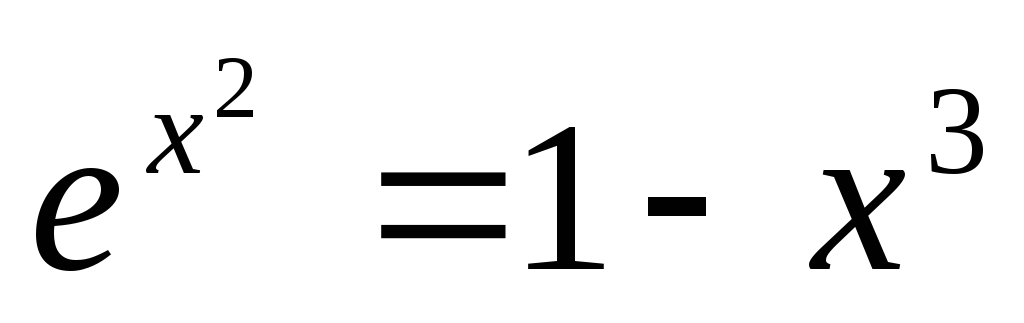
20	5x^2+2x-3=0	x^2+1=cos(x^2)
21	2x^2-5x-7=0
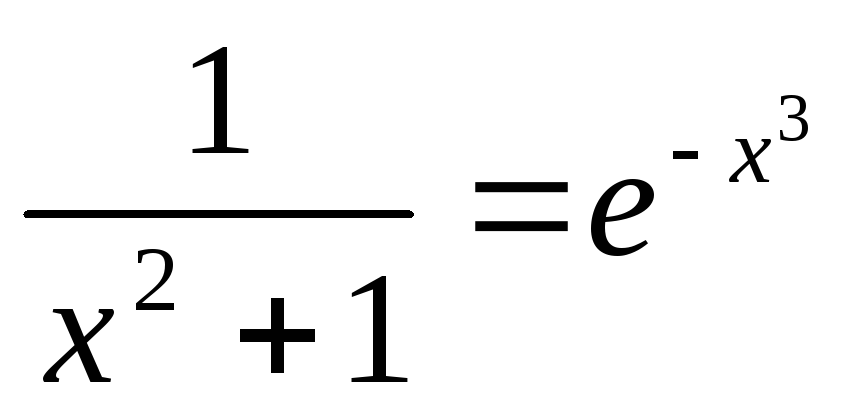
22	x^2-11x+20=0
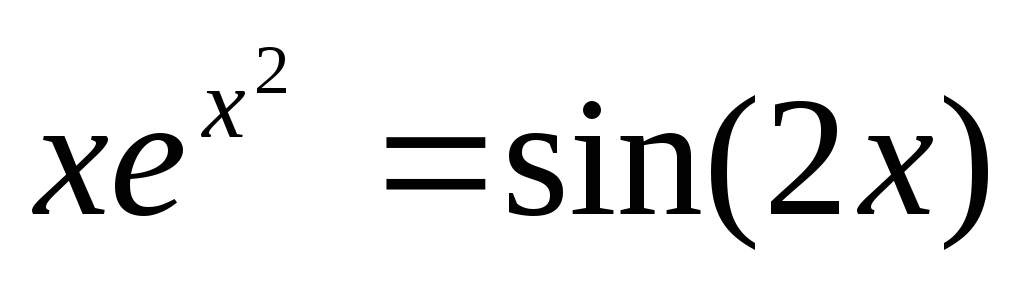
23	-x^2+6x-5=0
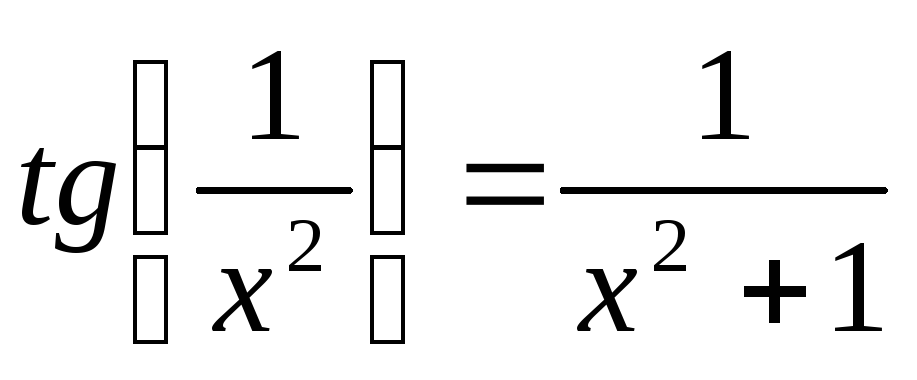
24	-x^2-5x+6=0	x^3+1=sin(x^3)
1	2	3
25	7x^2-10x-8=0
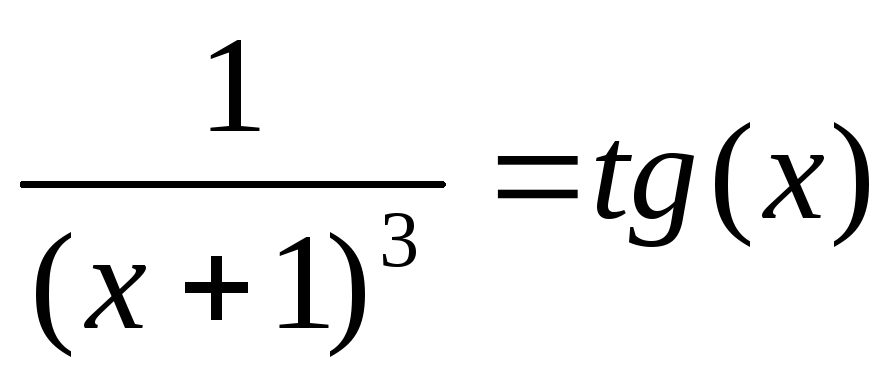
26	x^2+9x-28=0
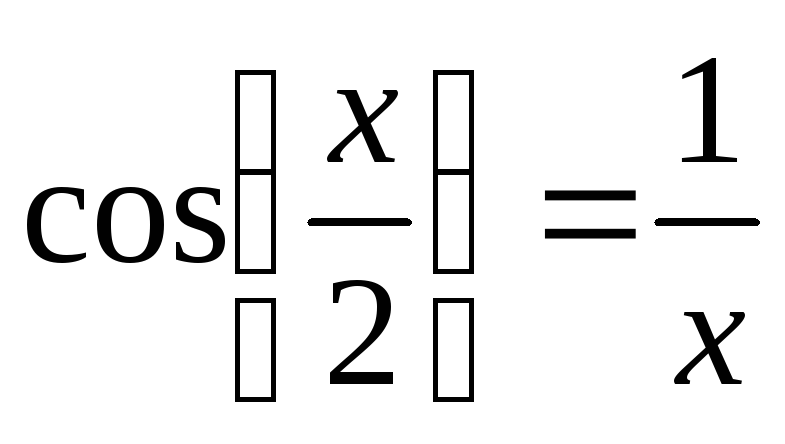
27	x^2-3x+1=0
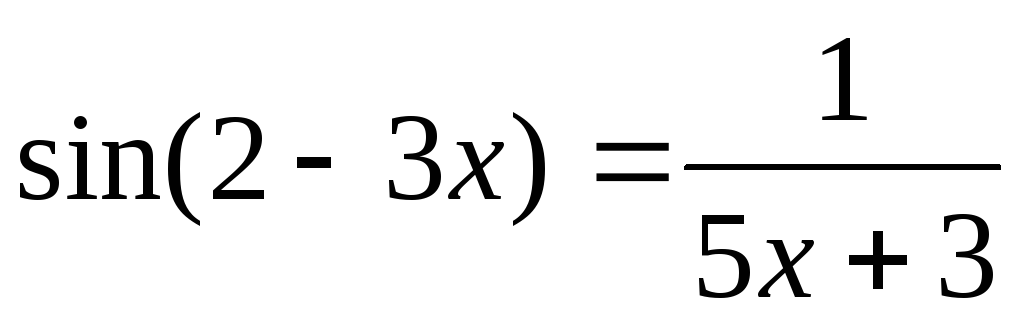
28	2x^2+3x-1=0
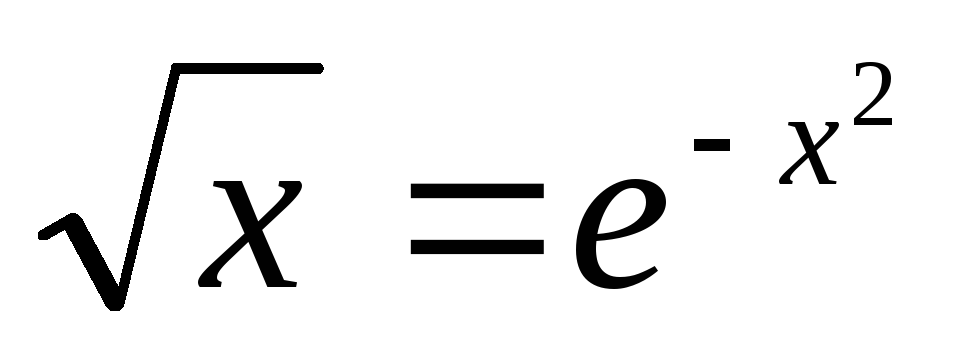
29	5x^2-15x-31=0	ln(3+x^2)=e^-x
30	7x^2-4x-23=0	x^2+1-6=cos(2x)

Таблица № 3.2: Варианты для лабораторной работы «Решение уравнений и систем»

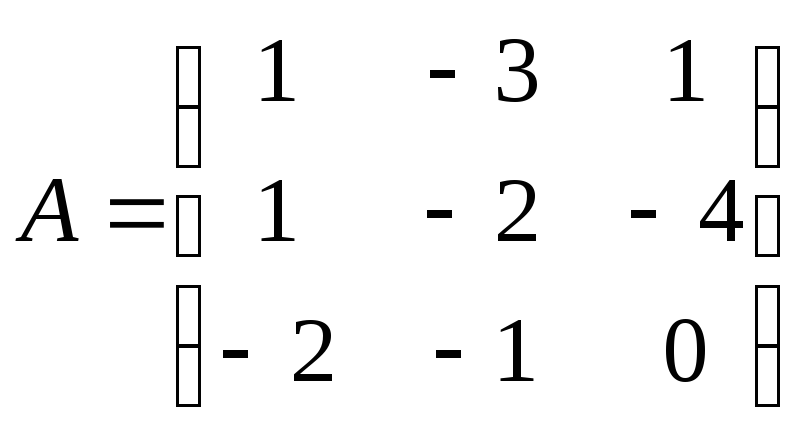
№ вар.	Матрица системы	Вектор правой части
1	2	3
1
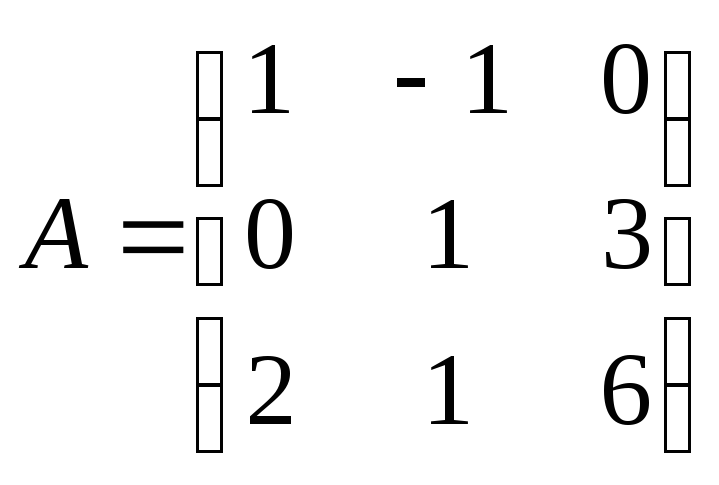
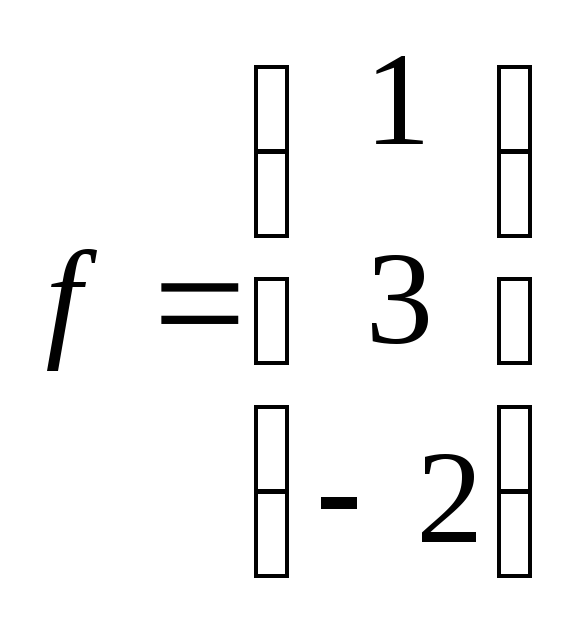
2
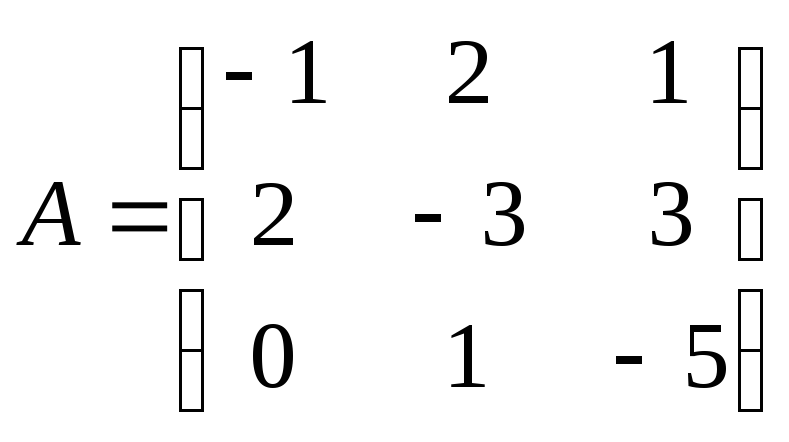
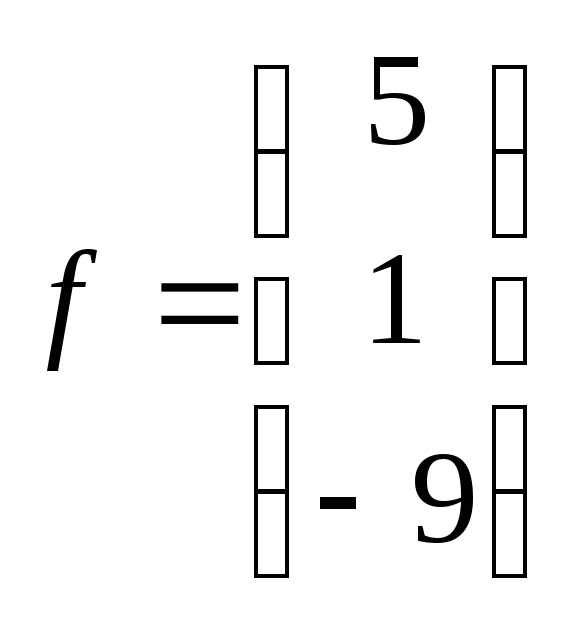
3
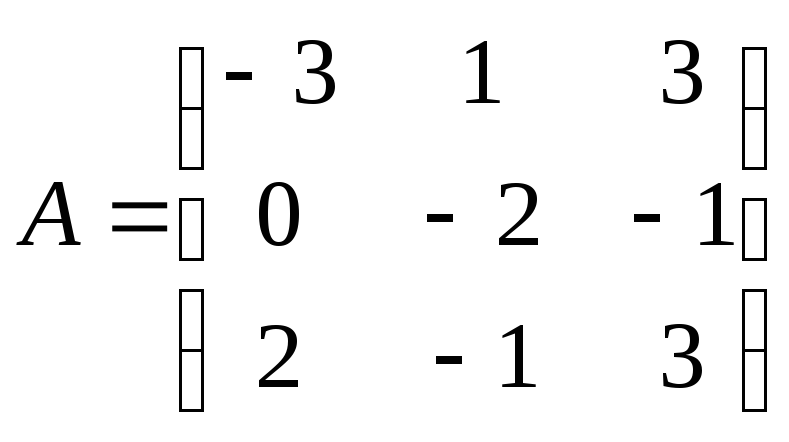
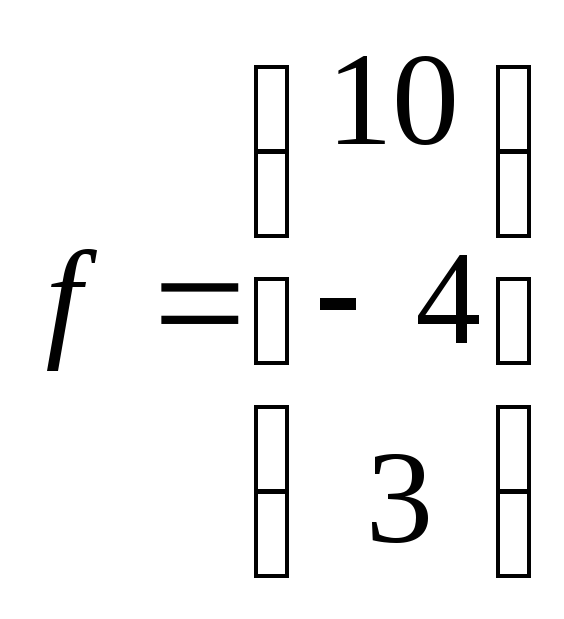
1	2	3
4
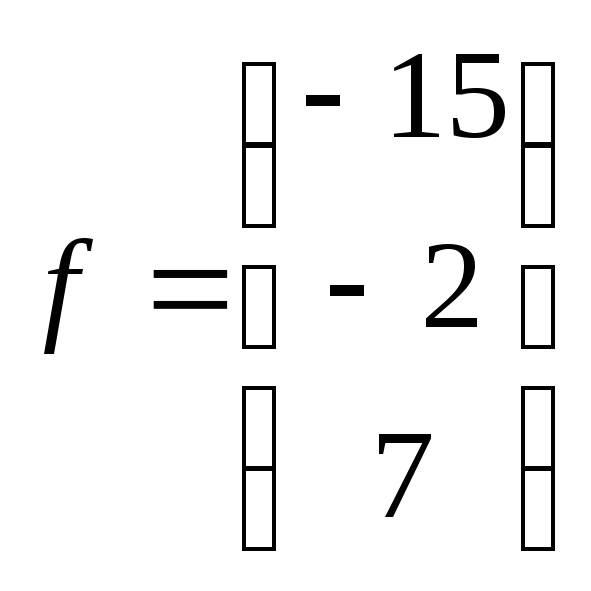
5
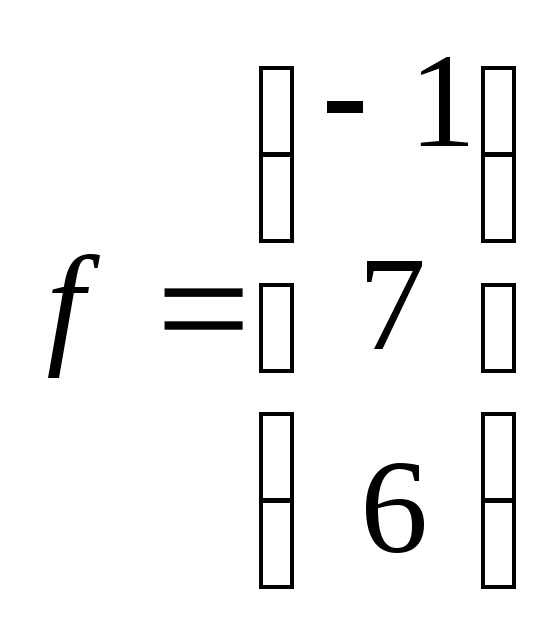
6
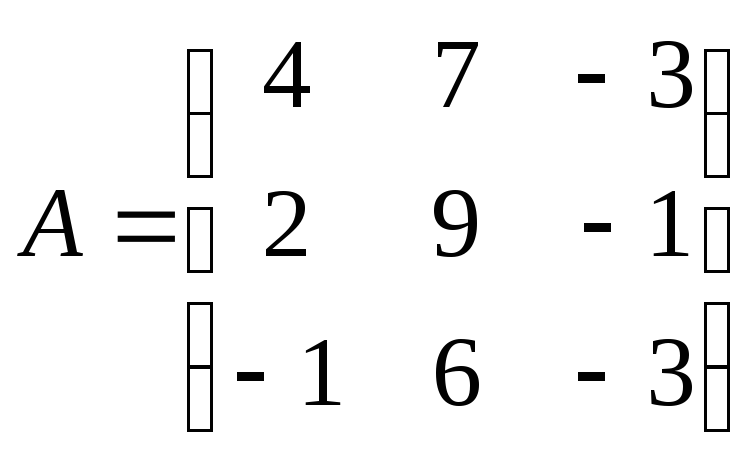
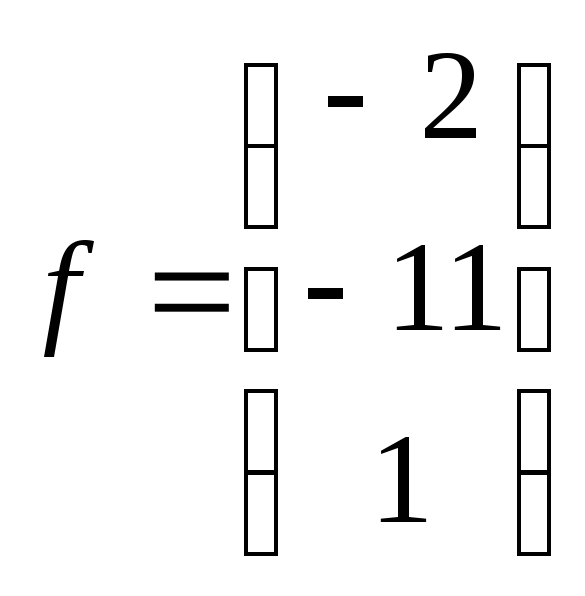
7
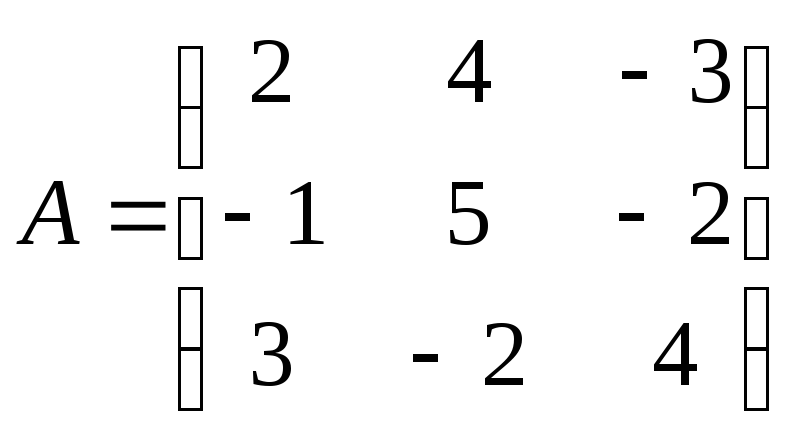
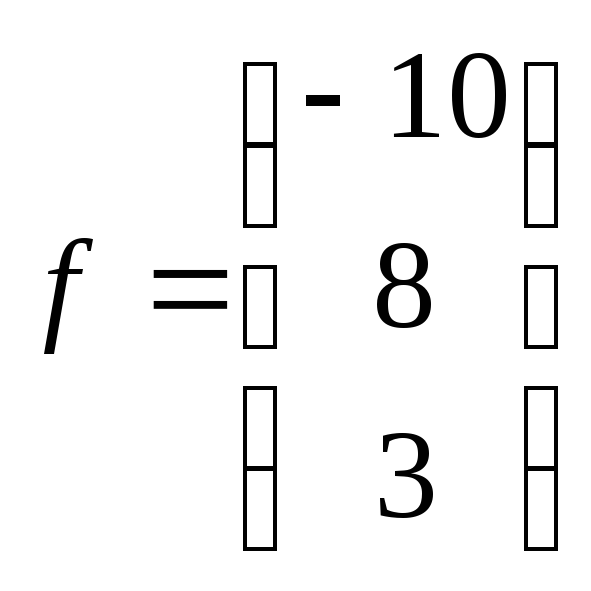
8
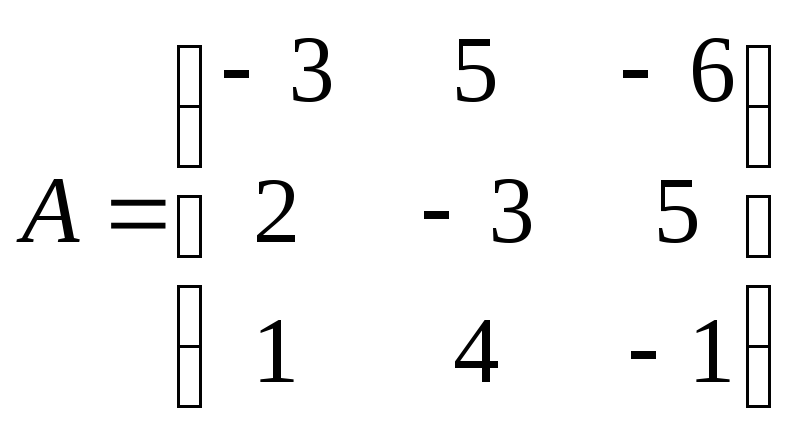
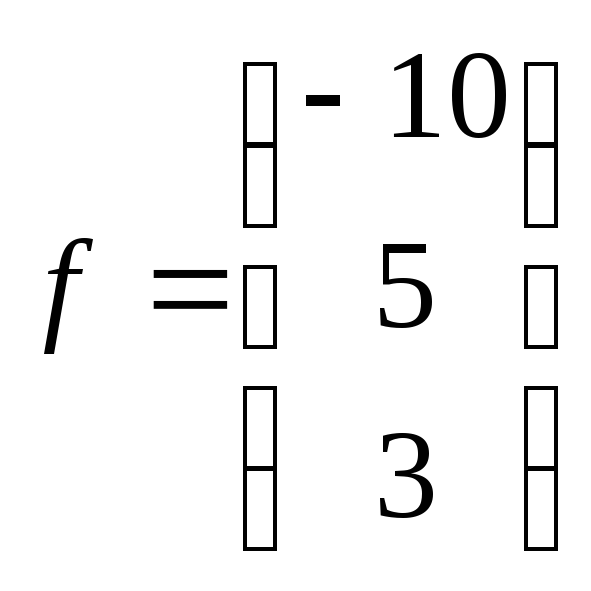
9
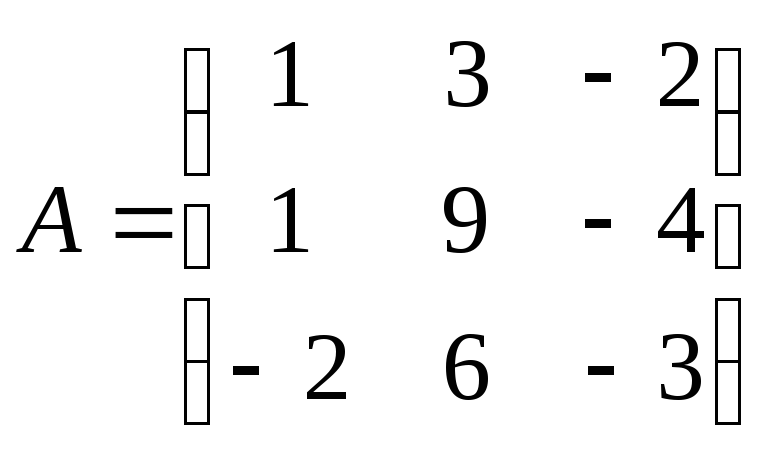
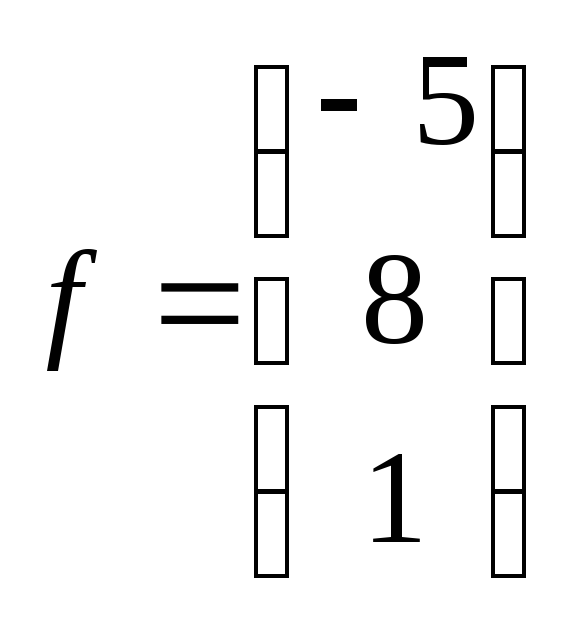
10
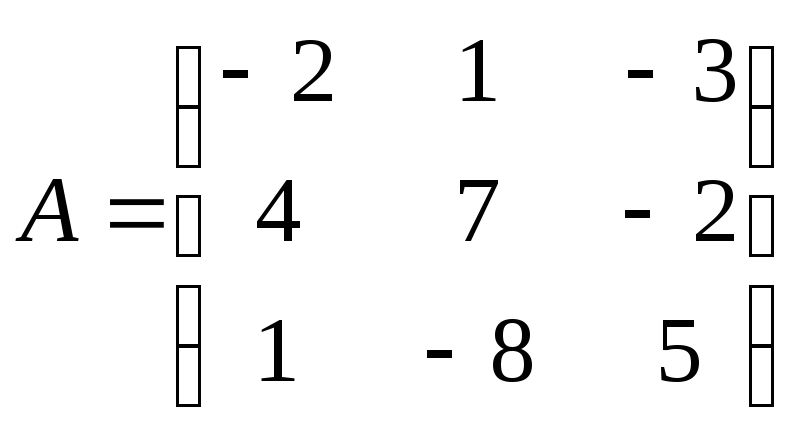
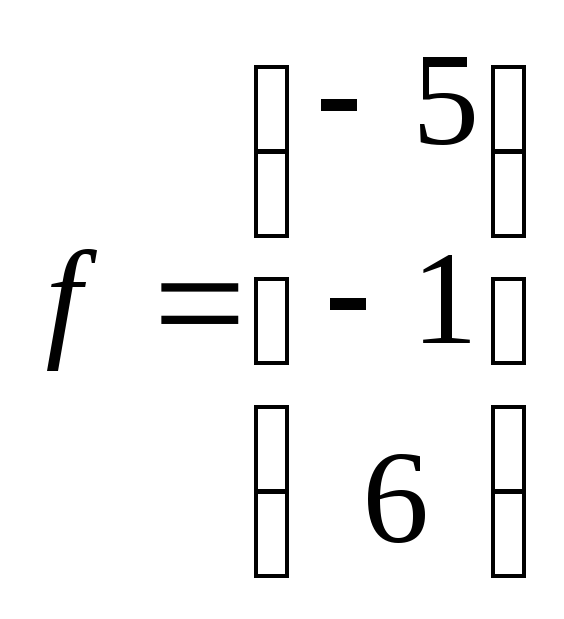
11
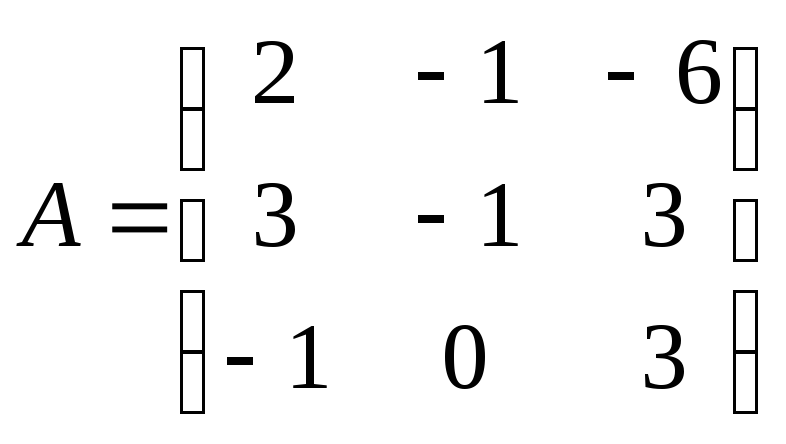
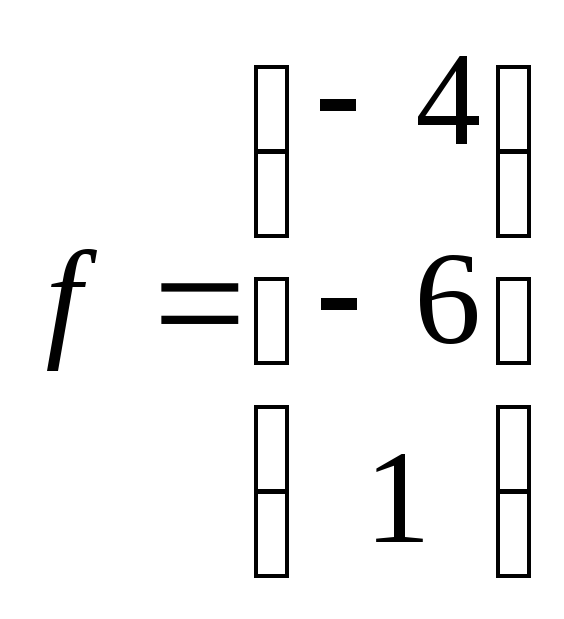
1	2	3
12
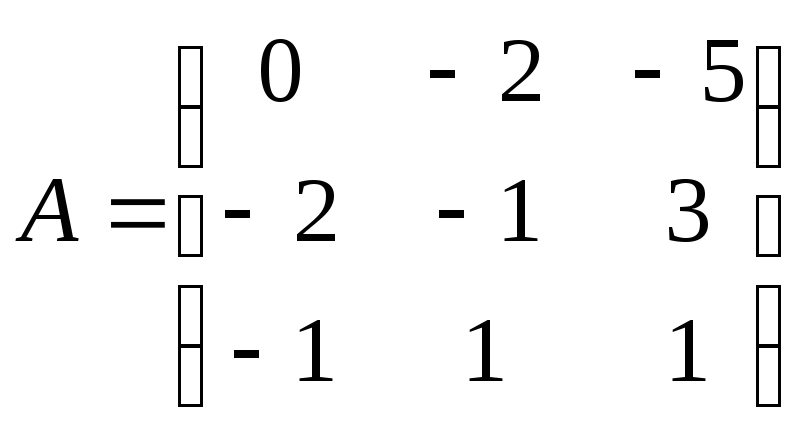
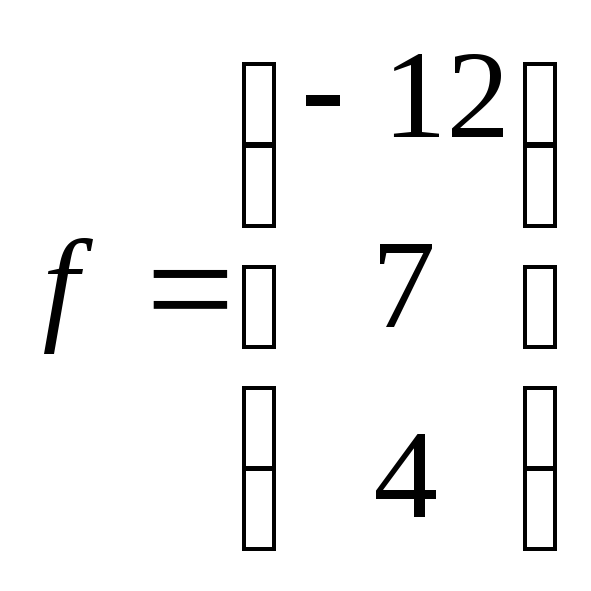
13
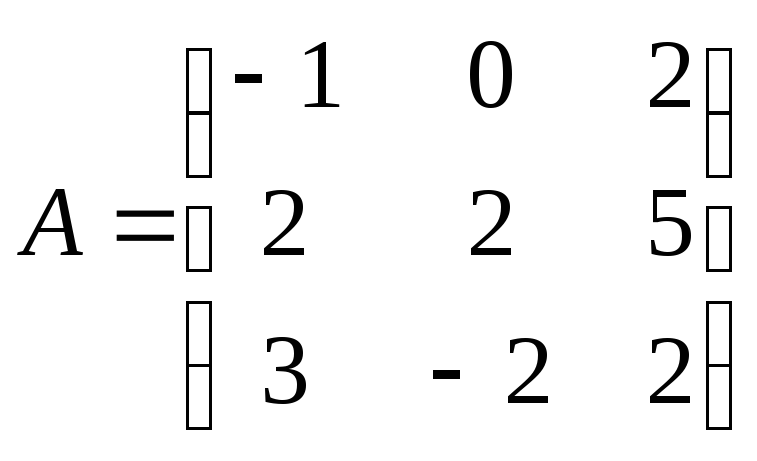
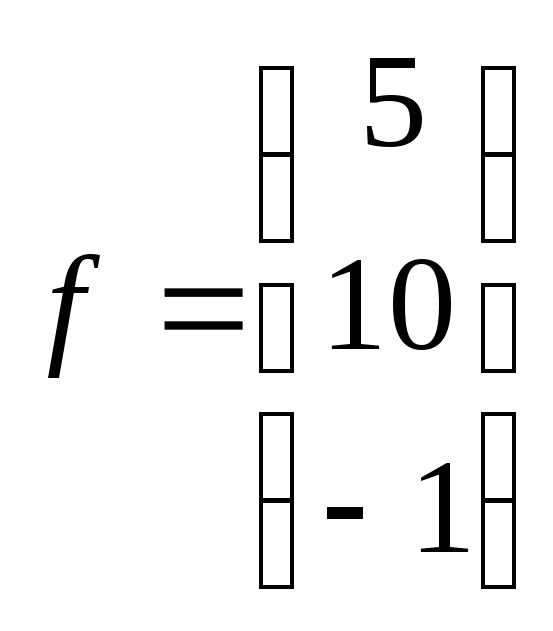
14
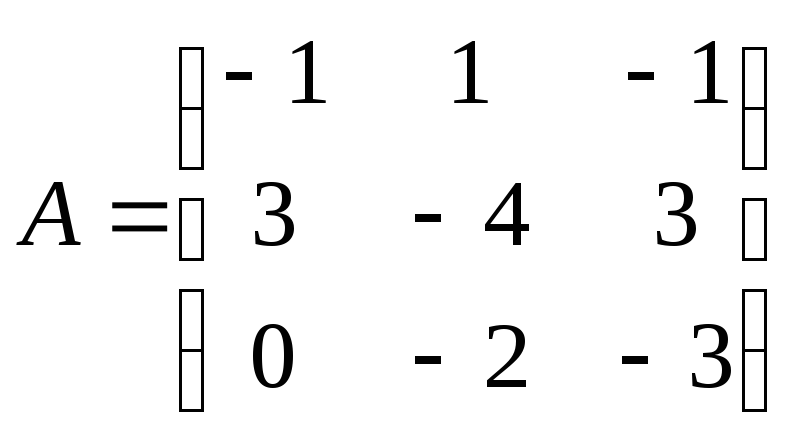
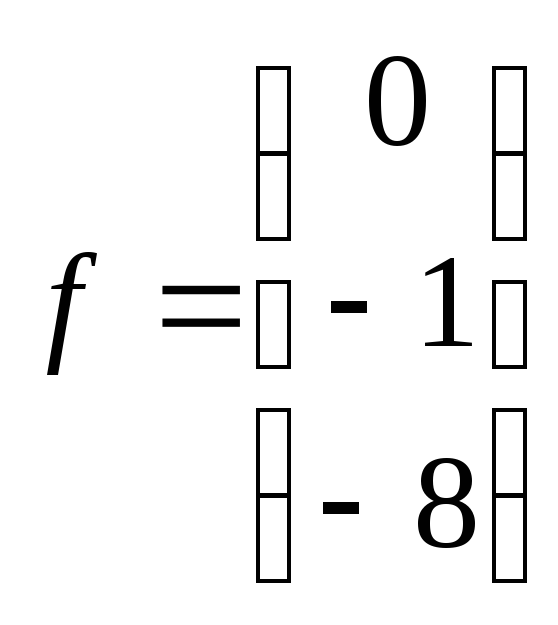
15
16
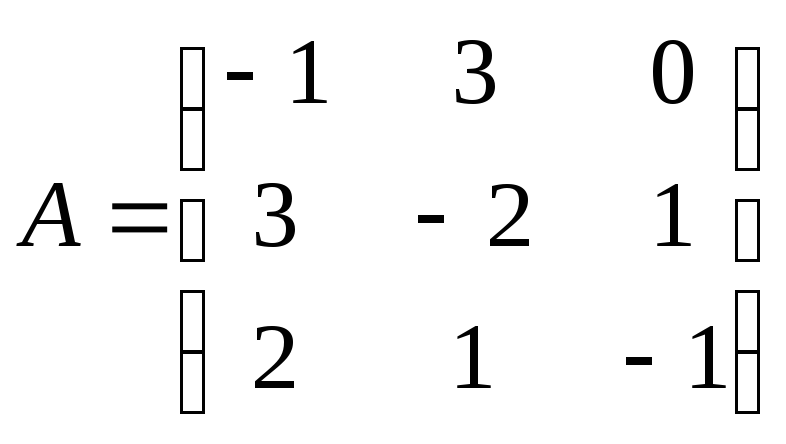
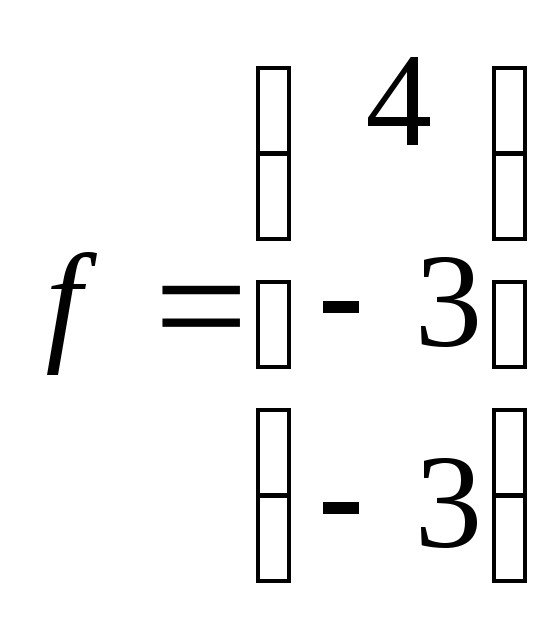
17
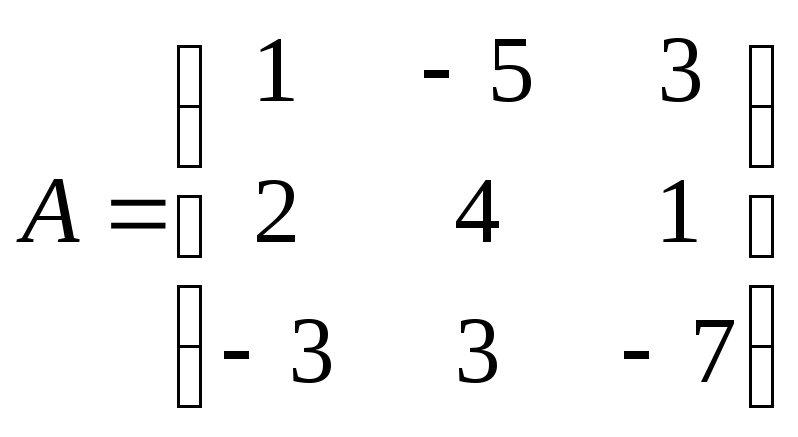
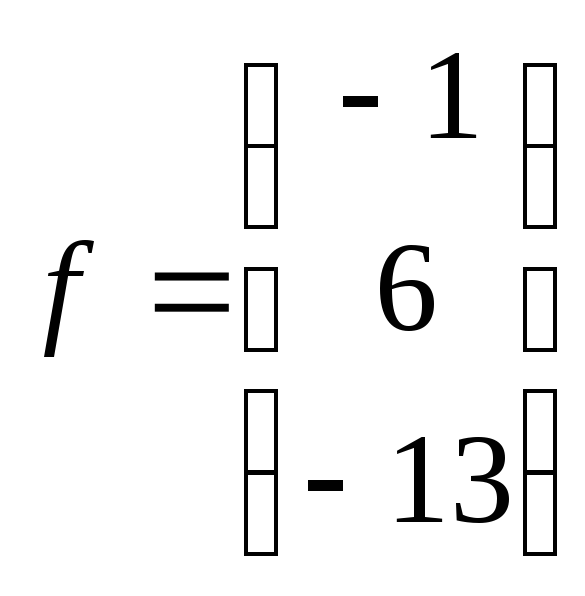
18
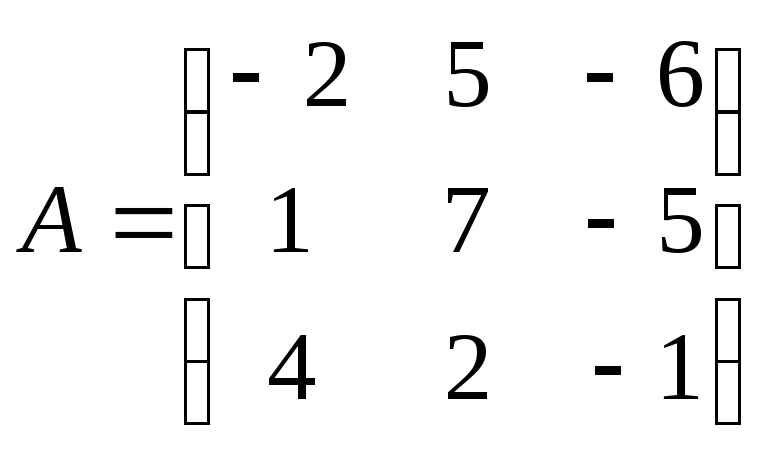
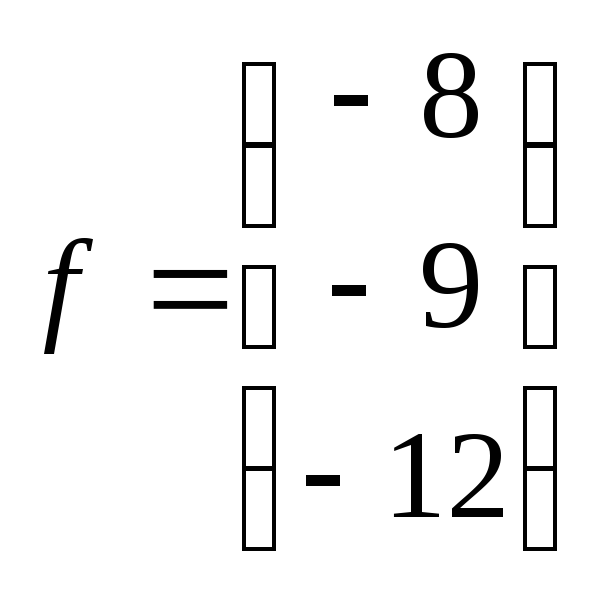
19
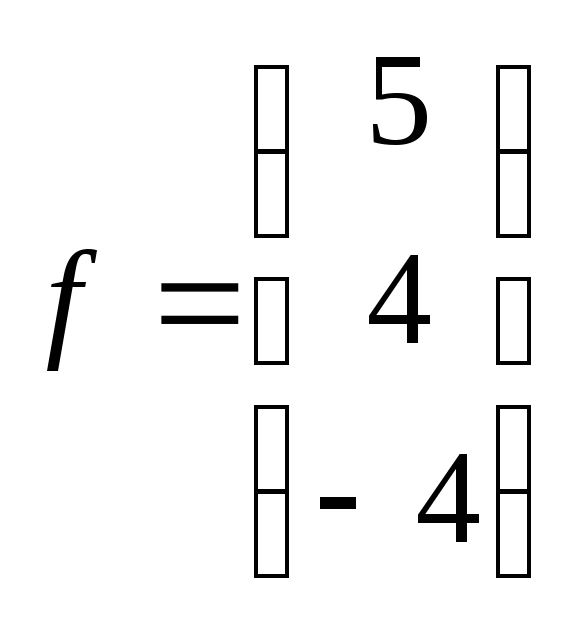
1	2	3
20
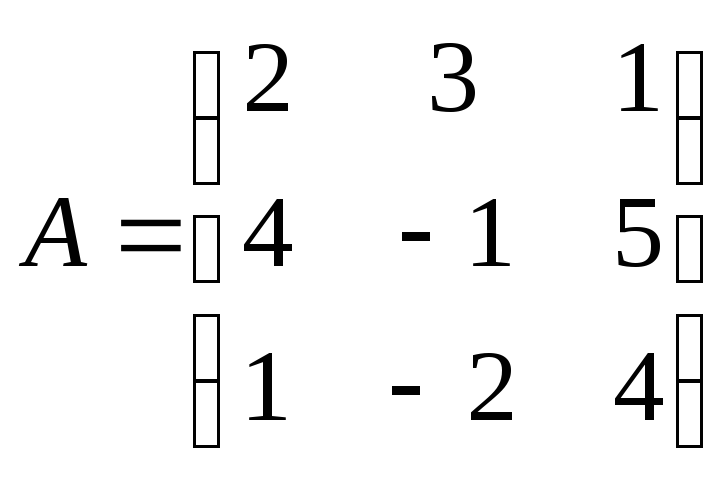
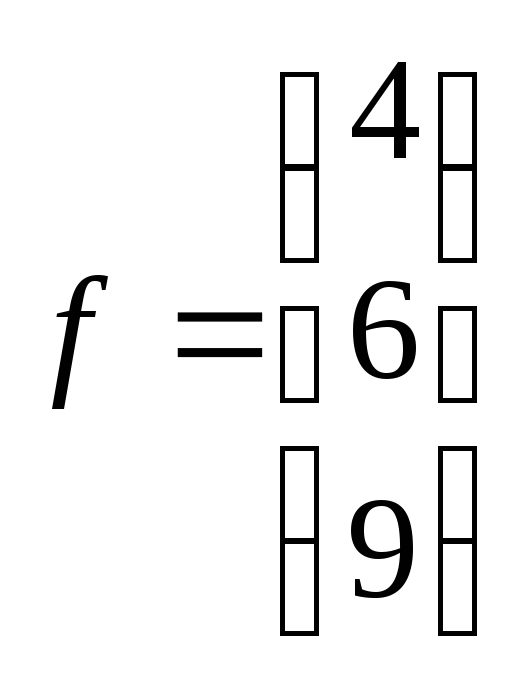
21
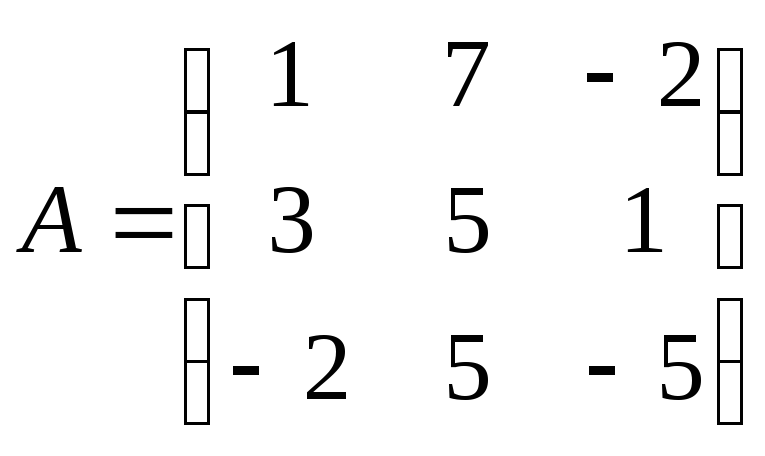
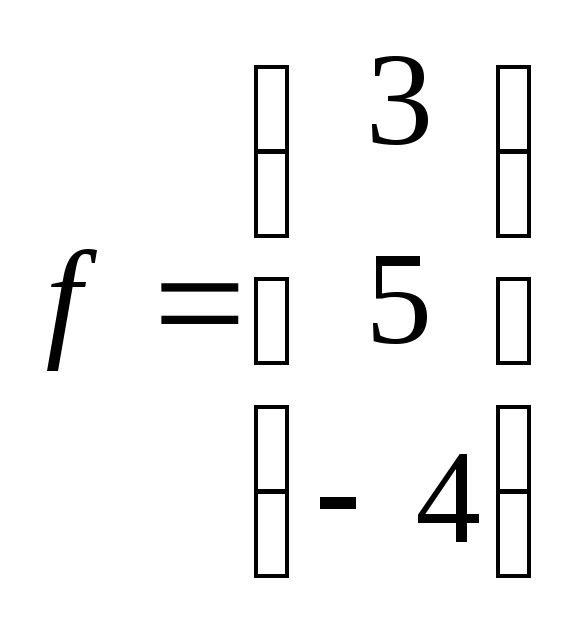
22
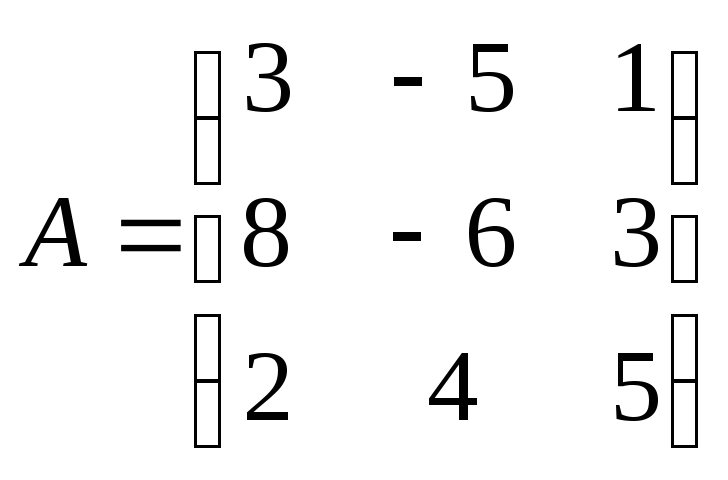
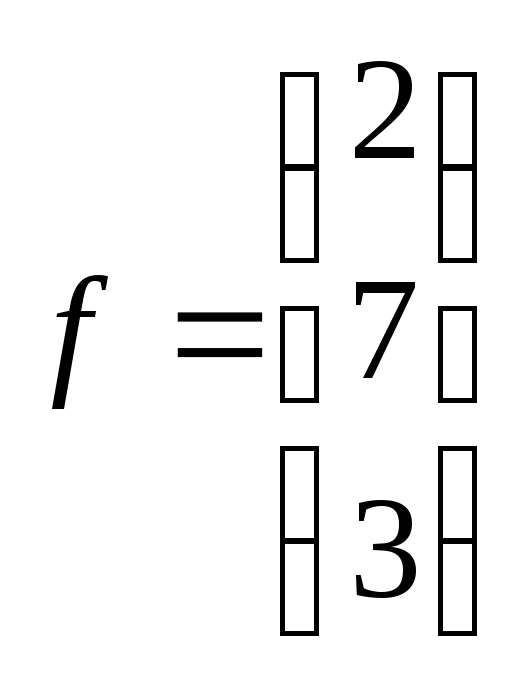
23
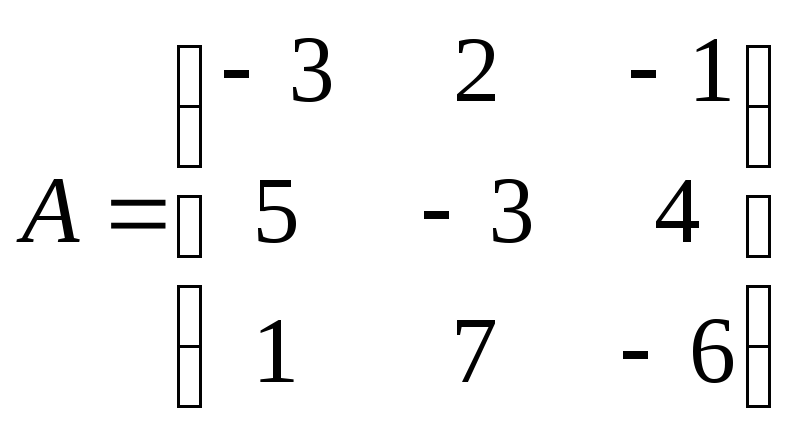
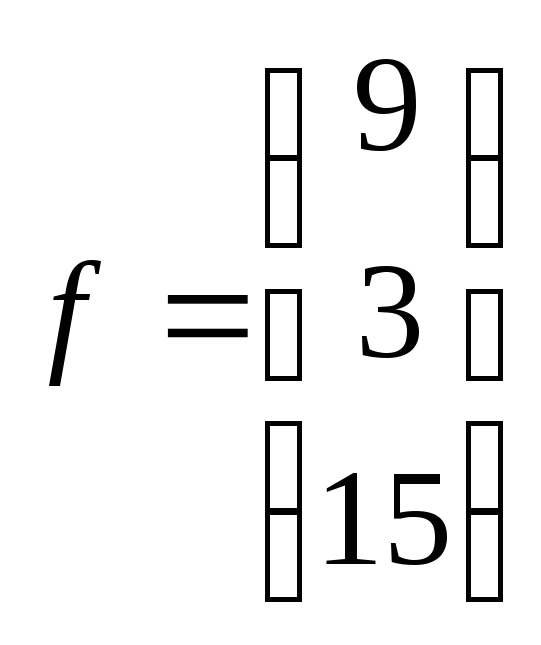
24
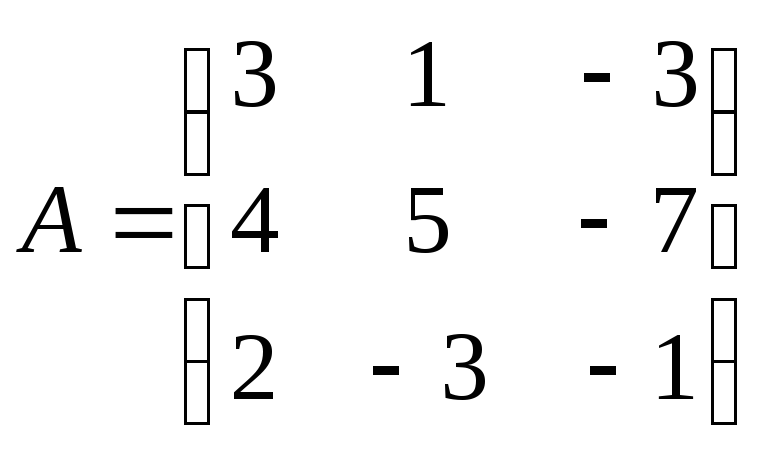
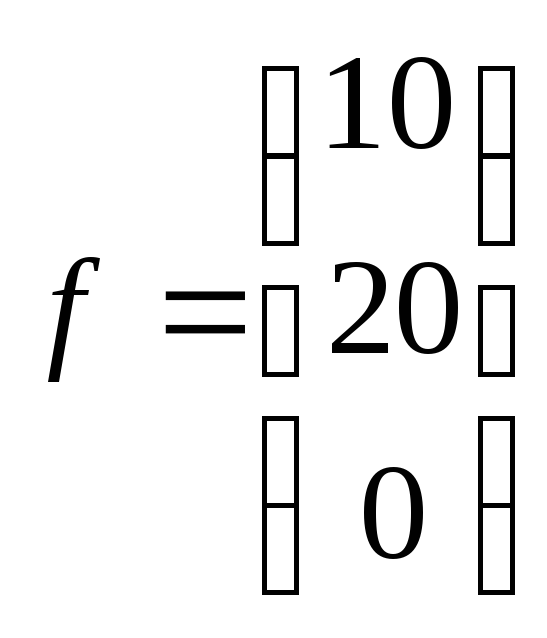
25
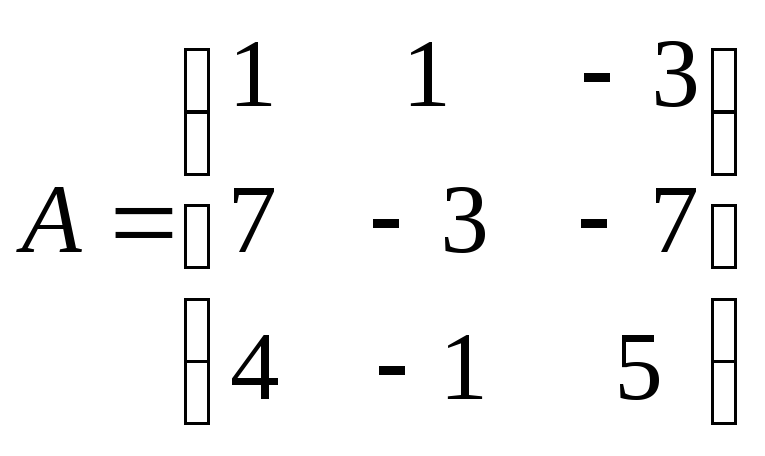
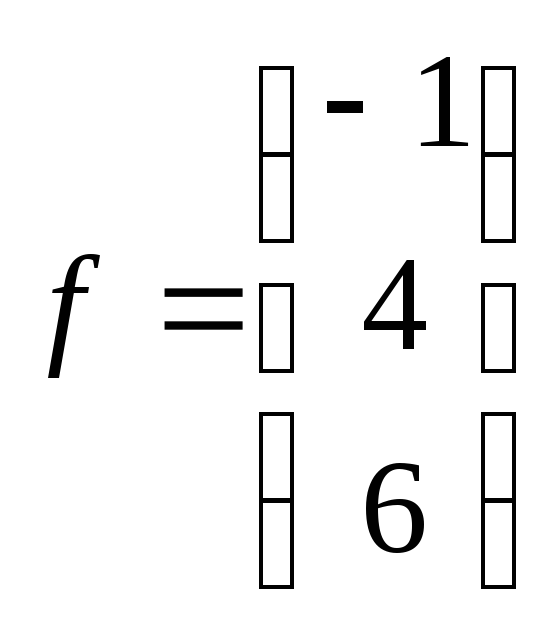
26
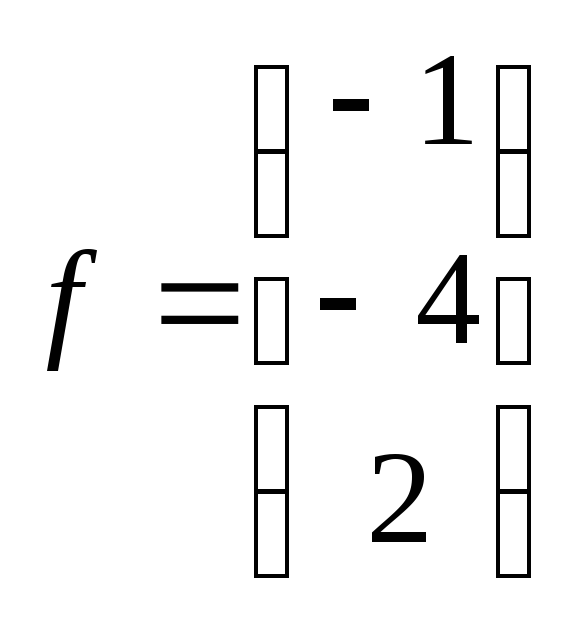
27
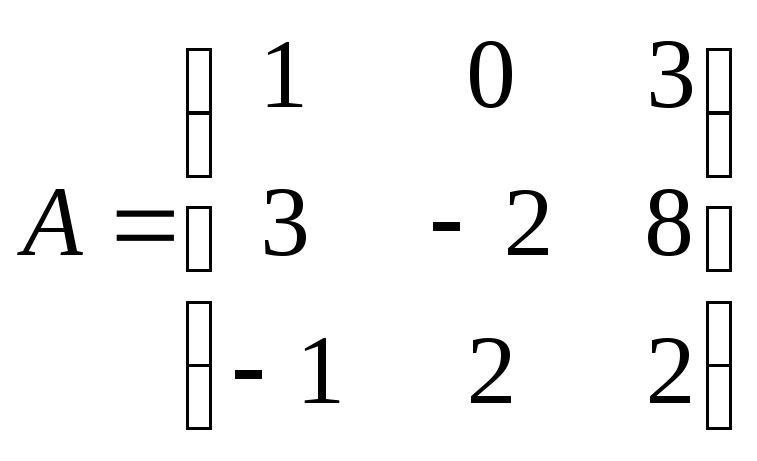
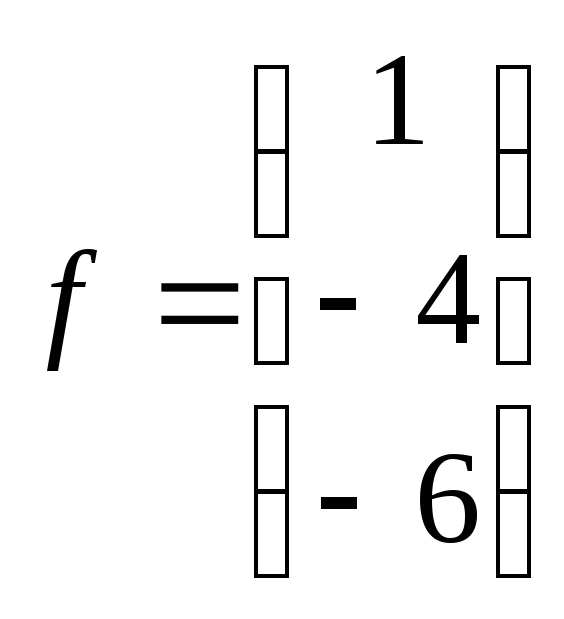
1	2	3
28
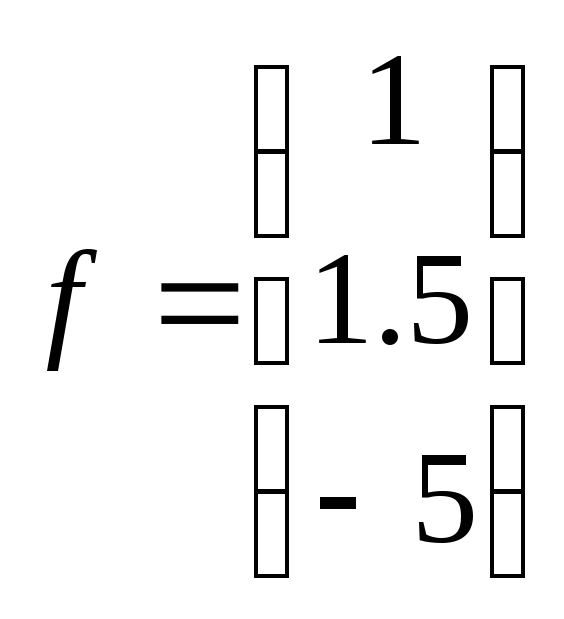
29
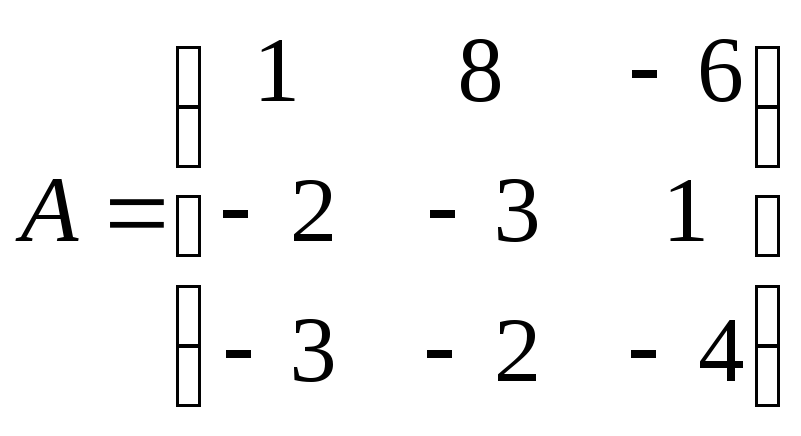
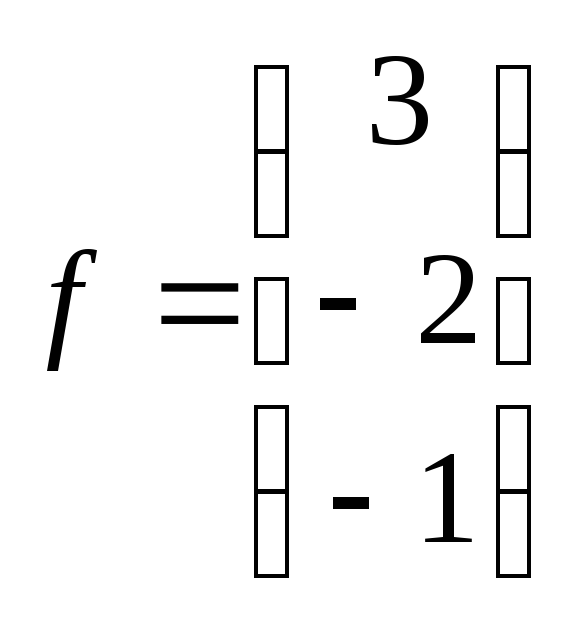
30

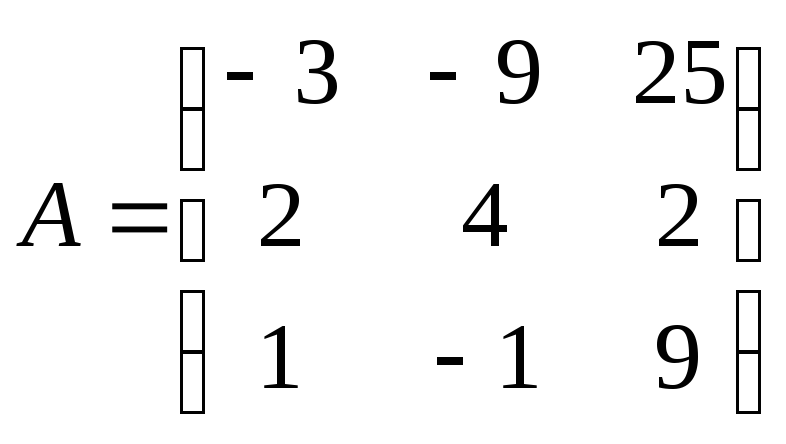
Пример выполнения задания:

Задание:

Уравнение n-ой степени	Трансцендентное уравнение
6x^3-25x^2-11x+60=0	e^2x+cos(3x)
Матрица системы	Вектор правой части

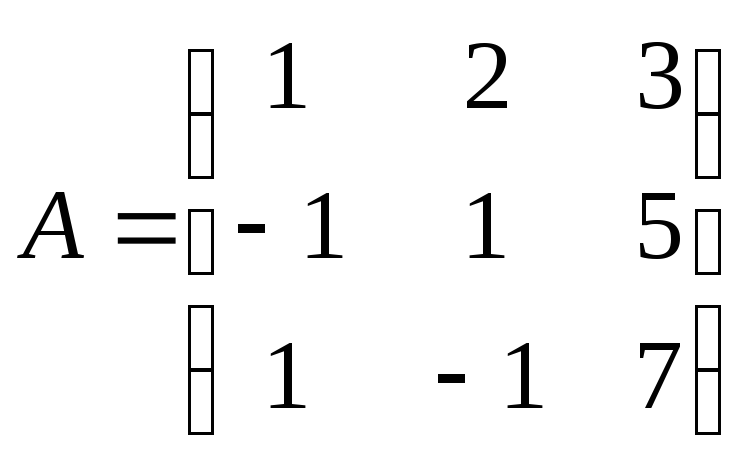
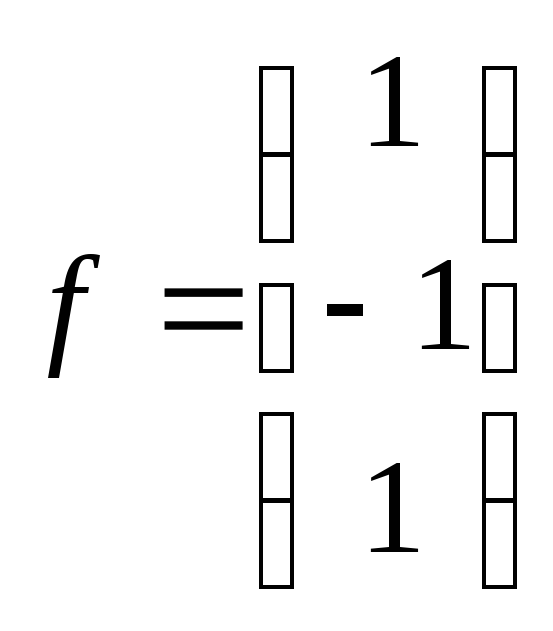
1. Найдем решение кубического уравнения. Для этого запишем его коэффициенты в следующем виде:

.

Определим полином

.

Найдем решение уравнения y(x)=0графически. Для этого построим график так, как это было описано в Лабораторной работе № 2, но для нашего графика мы не указываем границы по осиY(эти границыMathCadпроставляет сам). В результате получаем:

.

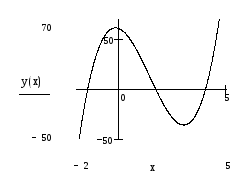
Мы видим, что наши корни лежат в интервалах: [-2; -1],[1; 2], [3; 4].

Получим корни уравнения y(x)=0аналитически. Для этого вMathCadпредназначена функцияsolveна панели инструментов «Символы». Имеем:

.

Можно убедиться, что наша оценка корней по графику была верной.

Для нахождения корней уравнений n-ой степени имеется специальная функцияpolyroots, в качестве параметра которой задается вектор коэффициентов:

.

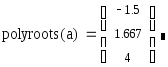В MathCadимеется функцияroot, которая позволяет находить корень из заданного интервала для любых уравнений. В частности для уравненийn-ой степени имеется два способа использования этой функции.

Примечание: В данной функции реализован метод Ньютона для нахождения корней уравнения, поэтому необходимо задавать начальное значение x, с которого и начинается поиск корня.

Первый способ.Задаем начальное значениеx:

.

Вызываем функцию:

,

где y(x)– заданная левая часть уравненияy(x)=0;x– приближенное значение аргумента;(–2)– левый край интервала, которому принадлежит искомый корень;(–1)– правый край интервала.

Для просмотра полученного значения достаточно набрать X11=, получим:

.

Оставшиеся два корня ищутся аналогично:

.

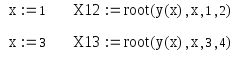В результате получим:

.

Второй способ.Задаем начальное значениеx:=-1и вызываем функцию:

.

Здесь интервалы не указываем, и функция ищет ближайший, к заданному значению, корень

.

Для нахождения второго корня задаем значение x:=1и исключаем из функции уже найденный корень:

.

Получили значение:

.

Третий корень ищем по аналогии:

.

2. Выполним проверку полученного решения:

.

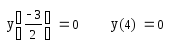
Мы видим, что корень из интервала [1; 2]более точно найден функциейsolve.

3. Трансцендентные уравнения можно решать графически, разбив уравнения на два более простых. Например, наше уравнение, заданное в виде

,

разобьем на два:

.

Построим графики этих уравнений

.

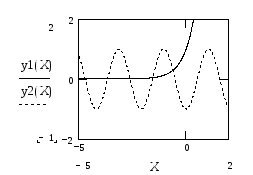
По графику видно, что все корни уравнения лежат в интервале (-;0).Найдем несколько корней при помощи функцииroot(интервалы можно подобрать по графику):

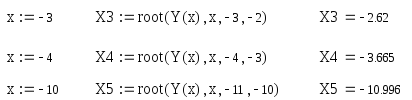
4. Выполним проверку полученного решения:

.

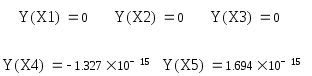Можно увидеть, что корни находятся с достаточно хорошей точностью, но с удалением от точки 0точность начинает ухудшаться.

5. Зададим систему уравнений матрицей Аи вектором правых частейf:

.

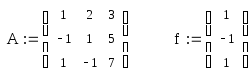Проведем исследование данной системы на разрешимость, для этого вычислим определитель матрицы А:

.

Так как определитель матрицы не равен нулю, следовательно, наша система разрешима и имеет единственное решение.

Получим данное решение графически. Для этого построим каждую плоскость отдельно. В MathCadплоскости задаются так

.

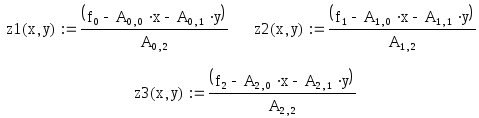Графическое представление этих плоскостей имеет вид

.

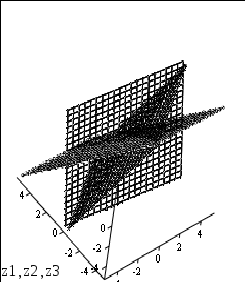Видно, что в пересечении мы получим одну общую точку для всех плоскостей, которая и будет решением данной системы.

6. Решим систему уравнений матричным методом. Для этого найдем обратную матрицу:

.

Теперь можно найти решение системы:

.

Вектор неизвестных имеет вид

.

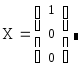7. Сделаем проверку:

.
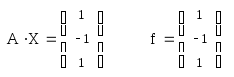