Лабораторная работа № 5 «Методы решения дифференциальных уравнений»

Цель работы:Познакомить читателя со встроенными возможностями пакетаMathCadдля решения дифференциальных уравнений (ДУ).

Рекомендуемая литература: [1-4, 6, 8-10].

Задание:

1. По заданной правой части ДУ первого порядка с разделяющимися переменными построить решение при помощи встроенных функций MathCad.

2. Построить разностную схему для ДУ из пункта 1.

3. Сравнить полученные в пунктах 1 и 2 решения.

4. Найти общее решение линейного неоднородного ДУ первого порядка.

5. Сделать проверку найденного в пункте 4 решения.

6. Найти решение неоднородного ДУ второго порядка с заданными начальными условиями.

Таблица № 5.1: Варианты лабораторной работы № 5 «Методы решения дифференциальных уравнений».

№	ДУ с разделяющи- мися переменными	Неоднородное ДУ первого порядка
1	2	3
1	y(0)=0.5 x[0; ]	y(0)=1
1	2	3
2	y(0)=3 x[0; ]	y(0)=1
3	y(0)=0.2 x[0; ]	y(0)=1
4	y(0)=1.5 x[0; ]	y(0)=1
5	y(0)=1.5 x[0; ]	y(0)=1
6	y(0)=0.5 x[0; ]	y(0)=1
7	y(0)=0.45 x[0; ]	y(0)=1
8	y(0)=0 x[0; 1]	y(0)=1
9	y(0)=0.25 x[0; ]	y(0)=1
10	y(0)=-1 x[0; 1]	y(0)=1
1	2	3
11	y(0)=1.5 x[0; ]	y(0)=1
12	y(0)=-1 x[0; 1]	y(0)=1
13	y(0)=0.35 x[0; ]	y(/2)=0
14	y(0)=-2 x[0; 1]	y(/2)=3
15	y(0)=0.15 x[0; ]	y(3)=1
16	y(0)=-1.5 x[0; 1]	y(2)=0
17	y(0)=0.45 x[0; ]	y(-2)=5
18	y(0)=-1 x[0; 1]	y()=1
1	2	3
19	y(0)=-0.5 x[0; ]	y(e)=0
20	y(0)=1.5 x[0; 1]	y(0)=4
21	y(0)=2.5 x[0; /2e]	y(0)=3
22	y(0)=1 x[0; 1]	y(1)=e
23	y(0)=1.5 x[0; ]	y(1)=e
24	y(0)=-1.5 x[0; 1]	y(0)=2
25	y(0)=0.5 x[0; ]	y(/2)=1
26	y(0)=-3 x[0; 1]	y(1)=1
1	2	3
27	y(0)=1 x[0; ]	y(3)=1
28	y(0)=-5 x[0; 1]	y(0)=3
29	y(0)=1 x[0; ]	y(0)=1
30	y(0)=2 x[0; 1]	y(1)=2

Таблица № 5.2: Варианты лабораторной работы № 5 «Методы решения дифференциальных уравнений».

№ вар.	Неоднородное ДУ второго порядка
1	2
1	y(0)=3 y’(0)=1/2
2	y(0)=-3 y’(0)=-1/5
1	2
3	y(0)=3 y’(0)=4/3
4	y(0)=0 y’(0)=3/4
5	y(0)=3 y’(0)=9
6	y(0)=1/4 y’(0)=0
7	y(0)=1 y’(0)=1
8	y(0)=1 y’(0)=3
9	y(0)=0 y’(0)=0
10	y(0)=-1 y’(0)=-3/2
11	y(0)=2/3 y’(0)=2
1	2
12	y(0)=2 y’(0)=3
13	y(0)=3 y’(0)=5
14	y(0)=1 y’(0)=4
15	y(0)=10 y’(0)=6
16	y(0)=3 y’(0)=4/3
17	y(0)=3 y’(0)=8
18	y(0)=-12 y’(0)=16
19	y(0)=2 y’(0)=6
20	y(0)=2/25 y’(0)=3/5
1	2
21	y(0)=3 y’(0)=1
22	y(0)=1 y’(0)=1/2
23	y(0)=1/3 y’(0)=1/2
24	y(0)=1 y’(0)=1
25	y(0)=1 y’(0)=2
26	y(0)=0 y’(0)=1
27	y(0)=1/2 y’(0)=0
28	y(0)=3 y’(0)=2
29	y(0)=1 y’(0)=1
30	y(0)=1 y’(0)=1/2

Пример выполнения задания:

Задание:

ДУ с разделяющимися переменными	Неоднородное ДУ первого порядка
y(0)=1 x[0; 2]	y(0)=1
Неоднородное ДУ второго порядка
y(0)=-8 y’(0)=3

1. ДУ первого порядка с разделяющимися переменными можно представить как:

,

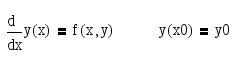где y(x)– неизвестная функция, а функцияf(x,y)– представляет собой неоднородную часть ДУ, которая здесь допускает представлениеf(x,y)=g(x)*h(y).

Для решения данного ДУ нужно задать правую часть f(x,y), начальные условия и интервал измененияx на котором следует найти решение,

.

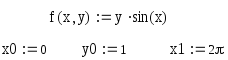Далее записывается блок решения ДУ, который начинается командным словом Given и формируется при помощи панели инструментов «Булево»:

,

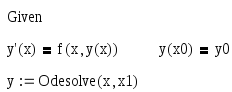где Odesolve(x,x1) – встроенная функция пользователя, которая формирует решение ДУ, заданного командным блокомGiven.x– переменная дифференцирования,x1– конечное значение интервала интегрирования.

2. Для записи разностной схемы ДУ необходимо задать количество итераций N, итерационный параметрiи шаг по переменной интегрированияdx:

.

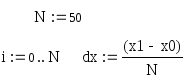Наберем вектор значений переменной интегрирования и начальное значение искомого решения y1:

.

Запишем разностную схему:

,

где вид правой части f(x,y)был задан выше.

Получаем, что разностное решение имеет вид:

.

3. Сравним два полученных выше решения графически:

.

Из графика следует, что при уменьшении параметра Nточность полученного в пункте 2 решения будет ухудшаться, а при увеличенииN– улучшаться.

4. Найдем решение неоднородного ДУ первого порядка, для этого запишем его в общем виде: y’=a(x)*y+b(x)и применим к нему готовую математическую формулу, которую можно найти в любой книге, посвященной решению обыкновенных ДУ [6]

, (2)

где С– константа интегрирования.

Заметим, что у нас и, запишем формулу (2) вMathCad:

.

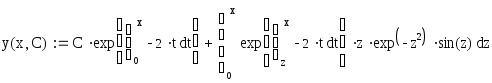Получим следующий результат:

.

Подставим начальное условие:

.

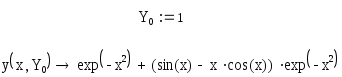Для графика полученного решения необходимо задать интервал изменения переменной xи шаг ее изменения:

.

Теперь можно построить график:

.

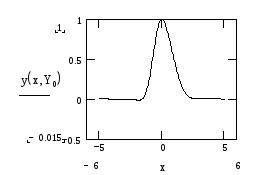
5. Сделаем проверку полученного в пункте 4 решения. Для этого подставим полученную функцию в исходное уравнение и воспользуемся символьной функцией simplify:

.

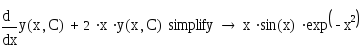Как мы можем убедиться, что полученный результат полностью совпадает с исходной правой частью.

6. Для решения неоднородного ДУ второго порядка, как и пункте 1, используется блок начинающийся с командного слова Given и встроенная функция пользователяOdesolve:

,

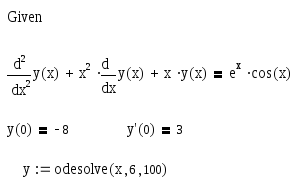где x– аргумент функции,6– конечное значение аргумента,100– количество шагов.

Для графического представления зададим x следующим образом

.

Тогда график y(x)примет вид

.