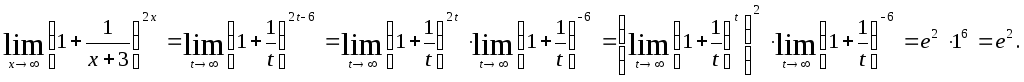Элементы аналитической геометрии

Пример. Даны координаты вершин пирамиды

.

Найти:

1) длину ребра А₁А₂;

2. угол между ребрами А₁А₂ и А₁А₄;

3. уравнения прямой А₁А_2;

4. уравнение плоскости А₁А₂А₃;

1) Найдем координаты вектора :

.

Длину вектора А₁А₂ найдем по формуле:

.

2) Вектор уже найден. Найдем вектор:

.

Скалярное произведение векторов инайдем по формуле:

.

Косинус угла между векторамиинайдем по формуле:

, .

3) Составим уравнения прямой А₁А₂, где . Воспользуемся уравнениями прямой, проходящей через две точки и:.

Принимая за точки исоответственнои, получим: .

Таким образом, — уравнения прямой.

4) Составим уравнение плоскости :

Пусть точка принадлежит плоскости. Рассмотрим векторыи найдем их координаты:

,,.

Так как данные вектора компланарны, то их смешанное произведение. Поэтому

Сократив на (26), получим уравнение . Это и есть уравнение плоскости.

Пример. Даны вершины треугольника :. Найти:

а) уравнения сторон треугольника;

б) систему неравенств, областью решений которой является множество точек, лежащих внутри и на границе треугольника.

Сделаем чертеж (рис.1)

а) Составим уравнения сторон треугольника . Воспользуемся уравнением:.

Так как точки принадлежат прямойАС, то

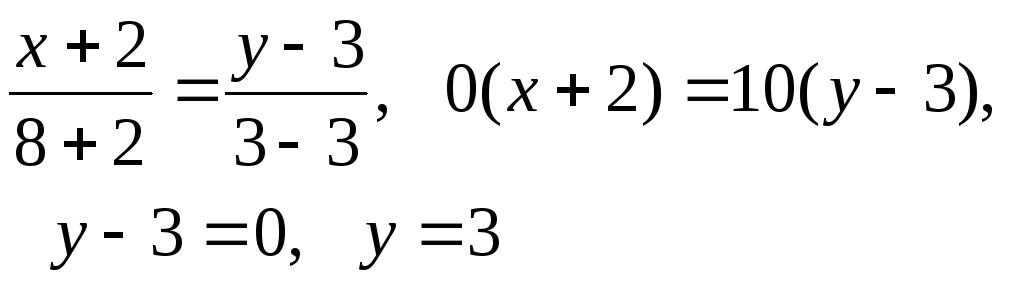
и — уравнение прямойАС.

Так как точки принадлежат прямойВС, то

, и

—уравнение прямой ВС.

Аналогично найдем уравнение прямой АВ: 7х+3у+5=0

б) Рассмотрим уравнение . Этому уравнению удовлетворяют точки, лежащие на прямойАВ. Начало координат, т.е. точка О(0,0) лежит внутри треугольника АВС и координаты точки О(0,0) удовлетворяют неравенству , так как. Поэтому и координаты всех точек, лежащих с той же стороны от прямойАВ, что и точка О, будут удовлетворять неравенству .

Уравнению удовлетворяют точки, лежащие на прямойАС. Координаты точки О(0,0) удовлетворяют неравенству , так как 03. Следовательно и все точки, лежащие с той же стороны от прямой АС, что и точка О будут удовлетворять неравенству .

Уравнению удовлетворяют координаты точек, лежащих на прямойВС. Координаты точки О(0,0) удовлетворяют неравенству , так как. Поэтому координаты всех точек, лежащих с той же стороны от прямой ВС, что и точка О(0,0), будут удовлетворять неравенству .

Таким образом, координаты точек, лежащих как внутри треугольника АВС, так и на его границах будут удовлетворять системе неравенств:

Линии второго порядка

Если центр окружности, эллипса, гиперболы или вершина параболы находятся в точке ,то соответствующие уравнения этих кривых будут иметь вид:

—окружность;

—гипербола;

—эллипс;

или — параболы.

Пример. Привести к каноническому виду уравнение линии второго порядка и построить эту линию .

Преобразуем уравнение, выделяя полные квадраты с переменными и:

,

,

,

,

—это уравнение гиперболы с центром в точке , действительная полуосьа=4, мнимая полуось (рис. 2).

Примеры решения заданий контрольной работы № 2 Пределы

Рассмотрим наиболее важные для практики пределы:

1. Если функция определена в точкеx = x₀, то ; 2.;

3. ; 4.– первый замечательный предел;

5.– второй замечательный предел ();

6. ; 7. .

Примеры. Найти пределы функций.

1. при а) х₀=3; б) х₀=.

2. ; 3..

Решение:

1. а) .

Подстановка предельного значения аргумента х₀=3 приводит к неопределенности вида .

Для раскрытия получившейся неопределенности найдем корни числителя: х₁=3 и х₂=; и корни знаменателя:х₁=3 и х₂=. Тогда применяя формулу

ах²+ bх+с=а(х-х₁)(х-х₂), получим:

2х²-5х-3==(х-3)(2х+1);

3х²-4х-15==(х-3)(3х+5).

После преобразования числителя и знаменателя, и сокращения дроби на (х–3) (до перехода к пределу), повторяем непосредственную подстановку предельного значения.

.

б) .

При х получаем неопределенность . Для раскрытия неопределенности разделим многочлены числителя и знаменателя на старшую степень аргумента, т. е. нах².

2. .

При вычислении пределов от тригонометрических функций обычно применяется первый замечательный предел: .

3.=.

Для того, чтобы применить второй замечательный предел, воспользуемся подстановкой t=х+3. Тогда x=t–3, 2x=2t–6 и, если , то и.

Таким образом,