
- •Содержание рабочей программы
- •Рекомендуемая литература
- •Правила выполнения и оформления контрольных работ
- •9. Теоретический материал и методические указания к выполнению контрольных заданий приведены в работе [10] - му № 2312.
- •5.11. 5.12.
- •Задания на контрольную работу № 2 Введение в математический анализ
- •8.1. 8.2. 8.3
- •Примеры решения заданий контрольной работы № 1 Матрицы и определители
- •Системы линейных уравнений
- •Метод обратной матрицы
- •Метод Жордана-Гаусса последовательного исключения переменных
- •Элементы аналитической геометрии
- •Линии второго порядка
- •Примеры решения заданий контрольной работы № 2 Пределы
- •Непрерывность функции
- •Производная фунции и её геометрический смысл
- •Правило Лопиталя
- •Исследование функций и построение графиков
Непрерывность функции
Определение.
Функция
![]() называетсянепрерывной
в точке х =
х0
, если она в этой точке определена и
называетсянепрерывной
в точке х =
х0
, если она в этой точке определена и
 .
.
Пример. Исследовать на непрерывность функцию
 .
.
Построим график этой функции (рис. 3).

Данная функция состоит из трех аналитических выражений, каждое из которых непрерывно в своей области. Поэтому функция может иметь разрывы только в местах перехода от одного аналитического выражения к другому, т.е. в точках х=0 и х=1.
Исследуем эти точки:
а) х=0:
![]() ;
;
![]() ;
;![]() .
.
Так как предел
функции при
![]() слева, равен пределу функции при
слева, равен пределу функции при![]() справа и равен значению функции прих=0,
то в этой точке функция непрерывна.
справа и равен значению функции прих=0,
то в этой точке функция непрерывна.
б) х=1:
![]() ;
;
![]() .
.
Так как предел
слева не равен пределу справа, то в точке
х=1
функция имеет разрыв 1-го рода, со скачком
![]() .
.
Производная фунции и её геометрический смысл
Пусть c=const, u=u(x), v=v(x) некоторые дифференцируемые функции, тогда справедливы следующие правила дифференцирования:
1.
![]() ;4.
;4.
![]() ; (2.1)
; (2.1)
2.
![]() ;
5.
;
5.
![]() (2.2)
(2.2)
3.
![]() ;
6.
;
6.![]() ;
;
если
![]() — сложная функция аргумента х
и
— сложная функция аргумента х
и
![]() или
или
![]() .
.
На основании определения производной и правил дифференцирования составлена таблица производных основных элементарных функций.
|
1. |
2. |
|
3. |
4. |
|
5. |
6. |
|
7. |
8. |
|
9. |
10. |
|
11. |
12. |
|
13. |
|
B приведенной таблице основных формул дифференцирования функций, переменная u может быть как независимой переменной, так и некоторой функцией от другой переменной.
Примеры. Найти дифференциалы функций:
1.
![]() ;
2.
;
2.![]() ;
3.
;
3.![]() ;
;
4.
![]() .
.
Решение.
1.
![]() .
.
Найдем производную данной функции:

Так как дифференциал
функции
![]() ,
получим:
,
получим:
![]() .
.
2.
![]() .
.
Найдем производную данной функции:

Следовательно,
![]() .
.
3.
![]() .
.
Найдем производную данной функции. Применяем формулу (2.1) производной произведения двух функций,

Следовательно,
![]() .
.
4.
![]() .
.
Найдем производную данной функции. Применяем формулу (2.2) производной частного двух функций,

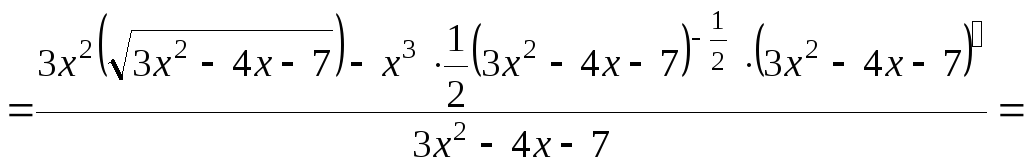

 .
.
Следовательно,
![]() .
.
Пример.
Составить уравнение касательной и
нормали к кривой
![]() в точке
в точке![]() .
.
Найдем значение
функции в точке x0,
![]() ;
производную функции
;
производную функции![]() и значение производной в точкеx0,
и значение производной в точкеx0,
![]() :
:
![]() ;
;
![]() ;
;![]() .
.
Так как уравнение
касательной, проходящей через т.![]() ,
имеет вид
,
имеет вид
![]() ,
получим:
,
получим:
![]() ;
;
![]() или
или![]() .
.
Уравнение нормали,
проходящей через т.![]() ,
имеет вид
,
имеет вид
![]() .
.
Для рассматриваемого случая получим:

![]() ;
;
![]() или
или![]() .
.
Сделаем чертеж (рис. 4).
Уравнение
данной линии запишем в виде
![]() или
или![]() .
Это парабола с вершиной в точке (2, 1) и
осью симметрии, параллельной осиОУ.
.
Это парабола с вершиной в точке (2, 1) и
осью симметрии, параллельной осиОУ.
Правило Лопиталя
Пусть функции
![]() и
и![]() определены, непрерывны и дифференцируемы
в некоторой окрестности точкиx0,
за исключением, может быть, самой точки
x0.
Причем в указанной окрестности производная
функции
определены, непрерывны и дифференцируемы
в некоторой окрестности точкиx0,
за исключением, может быть, самой точки
x0.
Причем в указанной окрестности производная
функции
![]() не равна нулю. Тогда, если
не равна нулю. Тогда, если и
и ,
или
,
или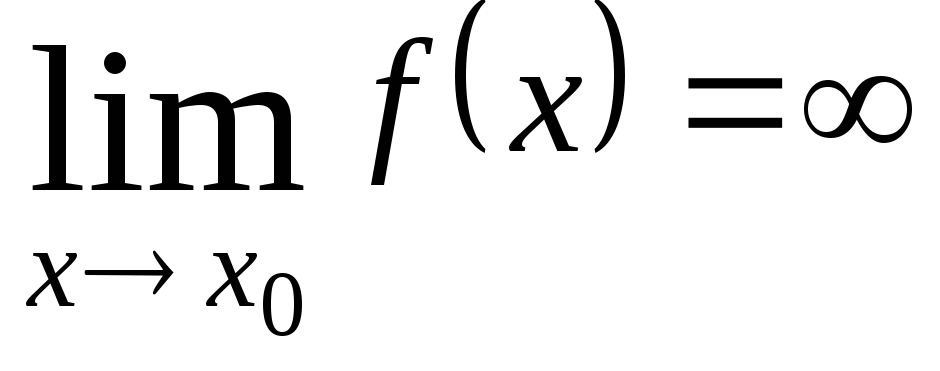 и
и ,
то предел отношения этих функций
представляет собой неопределенность
вида
,
то предел отношения этих функций
представляет собой неопределенность
вида![]() или
или![]() .
Если при этом существует предел отношения
производных данных функций и он равен
некоторому числуk,
то этому же числу равен предел отношения
самих функций. Это можно записать так:
.
Если при этом существует предел отношения
производных данных функций и он равен
некоторому числуk,
то этому же числу равен предел отношения
самих функций. Это можно записать так:
 .
.
При этом x0 может быть как конечным числом, так и бесконечностью.
Примеры. Найти
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() .
.
Решение.
1)
 .
.
 .
.
3)
![]()
 (напомним, что
(напомним, что
![]() ).
).
