Алгоритм симплекс-метода

Решение задачи ЛП симплекс-методом можно разбить на 3 шага.

1. Выбор начального базисного плана.

2. Проверка его на оптимальность. Если план оптимальный — задача решена. В противном случае —

3. Переход к новому базису.

Повторяя действия со второго шага, за конечное число шагов мы либо придем к оптимальному решению, либо убедимся в его отсутствии. Это означает конечность процедуры симплекс-метода.

I шаг. Выбор начального плана.

Пусть задача ЛП задана в канонической форме. Т.е. система ограничений состоит только из уравнений, правые части которых неотрицательны (т.е. ); и в каждом из них есть базисная переменная, т.е. переменная, которая с коэффициентом +1 содержится в одном уравнении и отсутствует во всех остальных; функция цели максимизируется.

Эти базисные переменные канонической задачи составят естественный начальный базисный план Х₁ при . Таким образом, начальный план задачи (1) содержится во втором столбце первой симплекс-таблицы (табл.1.), .

II шаг. Проверка плана на оптимальность.

Проверка плана на оптимальность заключается в анализе коэффициентов индексной строки (кроме d₀). Возможны 3 случая:

1. Все элементы индексной строки неотрицательны. Тогда записанный в этой таблице план Х₁ является оптимальным, = d₀ (см. табл. 1).

2. Среди элементов индексной строки есть отрицательные, но в столбце над ними нет ни одного положительного элемента. В этом случае целевая функция F не ограничена сверху на области планов и оптимального решения задачи не существует.

3. Среди элементов индексной строки есть отрицательные, и в столбцах над ними есть хотя бы один положительный элемент. Это означает, что целевая функция на плане Х₁ не достигла максимального значения и план может быть улучшен. Переходим к III шагу.

III шаг. Построение нового плана.

Каждый новый план отличается от предыдущего одной из базисных переменных. Переход к новому плану осуществляется преобразованиями Жордана-Гаусса, на каждом шаге которых один из базисных столбцов выводится из базиса и заменяется другим, небазисным. Алгоритм перехода к новому плану заключается в следующем.

1. Среди отрицательных элементов индексной строки выбираем наибольший по абсолютной величине (если таких несколько, можно взять любой из них). Соответствующий ему столбец называется ключевым столбцом, выделяем его. Переменная, соответствующая ключевому столбцу, войдет в новый базис, т.к. ключевой столбец переходит в число базисных.

2. Среди элементов ключевого столбца находим ключевой элемент. Для этого составляем отношения свободных членов к положительным элементам ключевого столбца; среди всех отношений выбираем минимальное. Знаменатель этого минимального отношения принимаем за ключевой элемент. Содержащая ключевой элемент строка соответствует переменной, которая выводится из базиса.

3. Все элементы строки, в которой находится ключевой элемент, делятся на значение ключевого элемента. Полученная строка называется ключевой строкой и записывается в новую таблицу на соответствующее место. Ключевую строку выделяем.

4. Остальные элементы новой таблицы (включая элементы индексной строки) находятся по правилу двух перпендикуляров: «прежнее значение элемента минус произведение чисел, стоящих на концах перпендикуляров, опущенных из этого элемента на ключевой столбец и ключевую строку».

Поясним сказанное на примере задачи (1).

Пусть в табл.1. отрицательный элемент d₂<0 индексной строки соответствует столбцу х₂. Тогда столбец х₂ является ключевым и пусть элемент a₂₂ — ключевой элемент, выделим их. Переменная х₄ выходит их базиса, ее место займет переменная х₂. Вторая строка плана будет ключевой, вычислим ее элементы и выделим.

Остальные элементы пересчитываются по правилу двух перпендикуляров, их значения приведены в таблице 2. Отметим, что элементы новой таблицы под ключевым столбцом равны 0, за исключением элемента в ключевой строке, который всегда равен 1, поскольку ключевой столбец становится базисным.

Таблица 2.

баз.	своб.	х1	х2	х3	х4
х3	b1	a11	a12	1	0
х4	b2	a21	a22	0	1
	d0	d1	d2	0	0
х3	b1- a12	A11- a12	0	1	- a12
х2			1	0
	d0–d2	d1–d2	0	0	–d2

В первую очередь целесообразно пересчитывать индексную строку, т.к. в случае оптимальности плана достаточно ограничиться вычислением элементов только второго столбца.

Пример 1. Составить математическую модель и найти решение следующей задачи.

Предприятие выпускает продукцию двух видов — I и II, используя для этого два вида сырья — S₁ и S₂. Количество сырья, необходимое для выпуска единицы продукции, запасы сырья и прибыль от продажи единицы продукции заданы в таблице. Необходимо составить план производства, при котором прибыль от продажи будет максимальной, при условии, что продукции II вида можно произвести не более 6 единиц.

Сырье	Расход сырья на ед. прод. вида		Запасы сырья
	I	II
S1	3	4	18
S2	1	4	14
Прибыль от продажи ед.прод.	1	2

Обозначим количество выпускаемой продукции I и II вида через х₁ и х₂ соответственно.

Первые два неравенства выражают ограничение объемов выпуска продукции наличными запасами сырья S₁ и S₂, третье неравенство соответствует ограничению количества продукции II вида. Функция цели — суммарная выручка от продажи продукции —максимизируется. Задача содержит две переменные и может быть решена графически, однако разберем на данном примере решение симплекс –методом.

Запишем задачу в каноническом виде. Правые части ограничений неотрицательны, знаки неравенств типа «», поэтому вводим в левые части неравенств дополнительные неотрицательные переменные со знаком «+» и получаем систему уравнений, в каждом из которых есть базисная переменная. , задача записана в каноническом виде.

Внесем данные в симплекс-таблицу (табл.3).

Таблица 3.

	0	0	1	2	0	0	0
	баз.	св.
0		18	3	4	1	0	0
0		14	1	4	0	1	0
0		6	0	1	0	0	1
		0	-1	-2	0	0	0	План X1
		4	2	0	1	-1	0
	х2	14/4	1/4	1	0	1/4	0
		5/2	-1/4	0	0	-1/4	1
	F	7	-1/2	0	0	1/2	0	План X2
	х1	2	1	0	1/2	-1/2	0
	х2	3
		3
	F	8	0	0	1/4	1/4	0	План X3

Базисными переменными в первом уравнении является переменная х₃ , во втором уравнении — переменная х₄, в третьем — переменная х₅.

Для вычисления элементов индексной строки припишем слева и сверху таблицы коэффициенты при соответствующих переменных целевой функции: коэффициент при х₁ равен 1, при х₂ равен 2, остальные переменные не содержатся в целевой функции, следовательно, коэффициенты при них равны 0. Найдем элементы индексной строки по формулам (2).

Поскольку в индексной строке есть отрицательные элементы (d₀ не рассматриваем), план X₁ не оптимален, следовательно, необходим переход к новому базису.

Наибольшим по модулю среди отрицательных элементов индексной строки является элемент –2, записанный в столбце . Это ключевой столбец, выделяем его. Ключевой столбец указывает переменную, вводимую в новый базис.

Найдем ключевой элемент. Для этого определим минимальное среди отношений свободных коэффициентов системы к положительным элементам ключевого столбца, . Знаменатель этого отношения есть ключевой элемент. Он находится во второй строке, которая становится ключевой, и указывает переменную, выходящую из базиса. Элементы ключевой строки плана X₂ получаются делением всех элементов второй строки плана X₁ на ключевой элемент, равный 4; в новой таблице второй строке соответствует переменная .

Остальные элементы нового плана X₂ находятся по правилу двух перпендикуляров. Заполнение новой таблицы рациональнее начинать с индексной строки, поскольку если все ее элементы окажутся неотрицательными, то план оптимален, и для остальных переменных достаточно будет вычислить лишь значения столбца свободных членов.

Индексная строка: ; ; 0 (т.к. соответствует базисному столбцу); ; ; . План не оптимален, считаем дальше.

Строка : ; ;0 (т.к. соответствует базисному столбцу); ; ; .

Строка : ; ; 0 (т.к. соответствует базисному столбцу); ; ; .

В таблице получены план X₂ и целевая функция . План X₂ может быть улучшен, т.к. в индексной строке есть отрицательный элемент –1/2. Он находится в первом столбце, следовательно, это новый ключевой столбец. Переменная входит в базис нового плана. Считаем отношения свободных членов к положительным элементам ключевого столбца и выбираем наименьшее: , знаменатель этой дроби определяет ключевой элемент, равный 2. Он стоит в первой строке, следовательно, эта строка становится ключевой, переменная выходит из базиса. Ключевая строка плана X₃ получается делением всех элементов первой строки плана X₂ на ключевой элемент, равный 2.

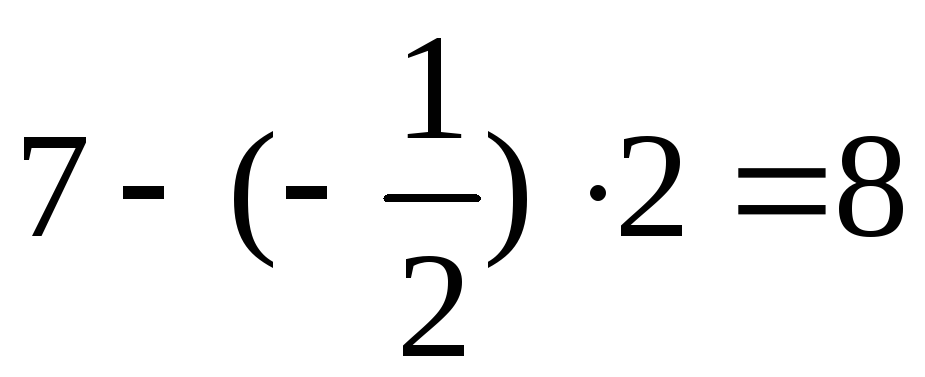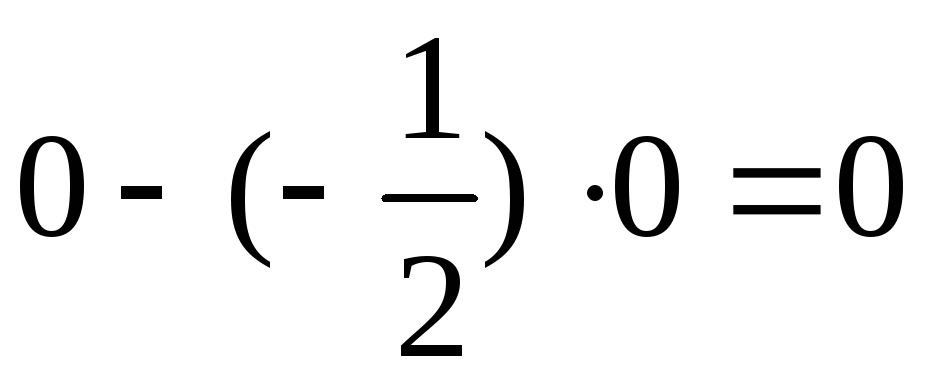Индексная строка: ; 0; ; ; ; . Поскольку в индексной строке нет отрицательных элементов, план X₃ оптимален и для него достаточно вычислить только значения базисных переменных.

По правилу двух перпендикуляров:

, .

В плане X₃ базисными переменными являются х_1, х₂, , остальные переменные — свободные, в базисном плане их полагают равными 0.

Выписываем оптимальный план задачи:

, .

Исходная задача содержала только две переменных, следовательно, окончательно, X^*(x₁,x₂)=(2;3). Отброшенная переменная означает «резерв» выпуска изделий II вида.

Предлагаем самостоятельно решить эту задачу графически и проверить себя по известному уже ответу.

Пример 2. Решить задачу ЛП:

Это общая задача, правые части ограничений неотрицательны. Сведем задачу к основной.

Первое ограничение уже дано в виде уравнения, в левую часть второго ограничения-неравенства для записи его в виде уравнения введем дополнительную переменную . В первом уравнении базисной переменной является х₃, во втором — переменная х_4. В исходной задаче целевая функция минимизируется. Поэтому введем функцию , для которой будем искать максимум: .

Получаем каноническую задачу:

Внесем условия в симплекс-таблицу (табл.4). Базисными являются переменные и .

Для заполнения индексной строки слева и сверху таблицы выпишем коэффициенты при переменных, входящих в целевую функцию, по формулам (2) вычислим элементы индексной строки:

Таблица 4.

		0	3	-1		-1		0
	Баз.	св.
-1		8	2		3		1	0
0		1	5		-2		0	1
	W	-8	-5		-2		0	0
		38/5	0		19/5		1	-2/5
	х1	1/5	1		-2/5		0	1/5
	W	-7	0		-4		0	1
	х2	2	0		1		5/19	-2/19
		1
	W	1	0		0		20/19	11/19

Начальный план не оптимален, т.к. среди элементов индексной строки есть отрицательные. Среди них наибольшим по модулю является элемент –5. Он стоит в столбце , следовательно, это ключевой столбец, переменнаявойдет в базис плана . Ключевой элемент равен знаменателю минимального из отношений: , т.е. 5. Ключевой элемент находится во второй строке. Следовательно, переменная уходит из базиса. Делим все элементы второй строки на 5 и получаем ключевую строку плана X₂ .

Остальные элементы плана X₂ находим по правилу двух перпендикуляров.

Индексная строка: ; 0;; 0; . План X₂ не оптимален, т.к. есть отрицательный элемент d₂ = –4.

Строка : ; 0; ; ; .

Отрицательный элемент d₂ = –4 индексной строки находится в столбце , следовательно, это ключевой столбец. Переменная войдет в базис нового плана. Из элементов ключевого столбца положителен только элемент, стоящий в первой строке и равный , он и будет ключевым, переменная выходит из базиса.

Разделим первую строку плана X₂ на и получим ключевую строку плана X₃. Вычислим элементы индексной строки: ;; 0; , . Поскольку в индексной строке нет отрицательных элементов, план X₃ оптимален и для него достаточно вычислить только значения базисных переменных.

По правилу двух перпендикуляров: .

В последней симплекс-таблице (табл.4) находится оптимальный план и . Исходная задача содержала две переменные, поэтому отбросим значения дополнительных переменных:,–W(X^*)=–1.

Окончательный ответ: , –1. 

Решение задачи линейного программирования

с искусственным базисом М-методом

Если среди уравнений-ограничений основной задачи ЛП есть такие, в которых отсутствует переменная, входящая в уравнения один раз с коэффициентом 1, то на первом шаге алгоритма симплекс-метода — построении начального плана — неизвестно, каким образом выбрать базис. В этом случае используют так называемый М-метод — метод искусственного базиса.

В уравнения, не содержащие базисной переменной, добавляют со знаком «+» неотрицательные переменные , называемые искусственными. Они образуют искусственный базис; чтобы отличать их от прочих переменных, сверху ставят значок «». Из целевой функции вычитают сумму искусственных переменных, умноженных на сколь угодно большое положительное число М, т.е. рассматривают Такая задача носит название М-задачи.

Справедлива следующая теорема.

1. Если в оптимальном решении М-задачи все искусственные переменные равны 0, то соответствующие значения остальных переменных дают оптимальное решение исходной задачи;

2. если в оптимальном решении М-задачи хотя бы одна искусственная переменная отлична от 0, то исходная задача планов не имеет;

3. если М-задача не имеет решения, то и исходная задача решения не имеет.

При решении задачи симплекс-методом для целевой функции отводят две строки: в первой записывают слагаемые , во второй — содержащие искусственные переменные . Преобразования совершаются с двумя строками, признак оптимальности сначала проверяется по второй строке. По ней же определяется переменная, подлежащая включению в базис. Процесс жордановых преобразований продолжают до тех пор, пока все искусственные переменные не будут выведены из базиса. По мере исключения искусственных переменных соответствующие им столбцы можно опускать, т.к. они в базис не возвращаются.

Согласно сформулированной теореме, если элементы второй индексной строки окажутся равными нулю, то исходная задача имеет решение. М-строку опускают и дальше решают обычную задачу с использованием первой строки целевой функции.

Пример 3. Составить математическую модель и найти решение следующей задачи.

Отдел технического контроля производит закупку нового оборудования — приборов трех типов, предполагая разместить их на площади 24 м². Каждый прибор первого типа занимает 2м², приборы второго и третьего типов — 1 и 3 м² соответственно. Эксплуатационные расходы составляют по 1 ден.ед. для оборудования первого и третьего типов, 4 ден.ед.— для второго типа. За смену приборы каждого типа способны проверить 2, 1 и 3 партии деталей соответственно.

Составить план закупки оборудования, позволяющий максимизировать количество проверенных за смену деталей, при условии, что необходимость в оборудовании первого и второго видов составляет не менее 6 единиц, а эксплуатационные расходы не должны превышать 20 ден.ед.

Обозначим количества оборудования первого, второго и третьего видов переменными соответственно. Тогда математическую модель задачи можно представить в виде:

где первое неравенство соответствует ограничению по эксплуатационным расходам, второе — по площади, третье — по количеству закупленного оборудования первого и второго типов. Функция прибыли максимизируется.

Запишем неравенства системы ограничений в виде уравнений. Правые части неравенств неотрицательны, в левые части введем дополнительные неотрицательные переменные: со знаком «+» в неравенства типа «» и со знаком «–» в неравенство типа «».

Система ограничений примет вид:

В первом уравнении базисной переменной является , во втором — переменная, а в третьем уравнении базисная переменная отсутствует ( входит со знаком «–»). Поэтому в третье уравнение вводим искусственную переменную, которая и будет являться базисной.

Решаем М-задачу:

^.

.

Внесем данные в симплекс-таблицу (табл.5). Базисными являются переменные , , .

Слева и сверху таблицы выпишем коэффициенты при переменных целевой функции. Для целевой функции отведем две строки таблицы: в первую строку запишем слагаемые без множителя М, во вторую строку будем записывать слагаемые с М, который вынесем в качестве общего множителя строки. Вычислим элементы индексной строки по формулам (4.2): d₀=. В первую строку записываем 0, во вторую — (–6). Далее: d₁=. Первое слагаемое вносим в первую, второе — во вторую индексную строку. Остальные элементы индексной строки вычисляются аналогично:

Анализируя вторую индексную строку, видим, что начальный план не оптимален. Выбираем в качестве ключевого, например, столбец . Ключевой элемент равен 1 и расположен в строке с искусственной базисной переменной , значит, она выходит из базиса.

Таблица 5.

		0	1	1		4	0	0	0	‑M
	Баз.	св.
0		20	1	4		1	1	0	0	0
0		24	2	1		3	0	1	0	0
-М		6	1	1		0	0	0	-1	1
		0	-1	-1		-4	0	0	0	0
	M	-6	-1	-1		0	0	0	1	0
		14	0	3		1	1	0	1
		12	0	-1		3	0	1	2
	х1	6	1	1		0	0	0	-1
		6	0	0		-4	0	0	-1
	M	0	0	0		0	0	0	0
		10	0	10/3		0	1	‑1/3	1/3
	x3	4	0	‑1/3		1	0	1/3	2/3
		6	1	1		0	0	0	-1
		22	0	‑4/3		0	0	4/3	5/3
	х2	3	0	1		0	2/10	‑1/10	1/10
	x3	5
		3
		26	0		0	0	4/10	6/5	9/5

Элементы второй симплекс-таблицы находятся обычными преобразованиями, элементы каждой из двух индексных строк находятся по правилу двух перпендикуляров. Базис во второй симплекс-таблице не содержит искусственной переменной, поэтому из дальнейшего рассмотрения столбец исключаем. Вторая индексная строка содержит нулевые элементы, ее также исключаем. Об оптимальности плана судим по первой индексной строке. Она содержит отрицательные элементы, следовательно, план Х₂ не оптимален, переходим к плану .

План оптимален, . Отбрасывая дополнительные переменные, получим окончательный ответ: X^*=(3;3;5) и .

Пример 4. Cоставить математическую модель и найти решение задачи.

При кормлении животных используются три вида корма А, В и С, в каждом из которых содержатся питательные вещества в количестве 2, 6, 7 г/кг и в количестве 2, 4, 5 г/кг соответственно. Стоимость 1 кг кормов А, В и С составляет 1, 3 и 2 ден.ед. Составить суточный рацион кормления животных, при котором расходы будут минимальны, если ежедневно они должны потреблять 10 кг пищи, получая при этом не менее 28 г питательного вещества и не более 36 г вещества .

Составим математическую модель задачи. Обозначим количество кормов вида А, В и С неизвестными (кг). Тогда математически условие задачи можно записать в виде:

Это общая форма задачи ЛП, запишем ее в виде основной формы. Правые части неравенств и уравнения в системе ограничений неотрицательны, в левые части неравенств введем дополнительные неотрицательные переменные: со знаком «+» в неравенство типа «» и со знаком «–» в неравенство типа «». Минимизацию функции заменим максимизацией функции .

Исходная задача примет вид:

В первом уравнении базисная переменная отсутствует, введем в левую часть искусственную неотрицательную переменную, которая будет базисной. Второе уравнение содержит базисную переменную . В третьем уравнении базисной переменной нет, введем в левую часть искусственную неотрицательную переменную . Поскольку задача с искусственным базисом, из целевой функции вычитаем .

Таким образом приходим к М-задаче:

Внесем данные в симплекс-таблицу. Для функции отведем две строки таблицы. В первую будем вписывать коэффициенты целевой функции, не содержащие число М, во вторую — со множителем М, который вынесем в качестве общего множителя строки.

Отрицательные элементы второй индексной строки свидетельствуют о том, что план не оптимален (каждой симплекс-таблице соответствует свой план, указание которого в самой таблице в дальнейшем опускаем). Ключевым столбцом является столбец . Ключевой элемент равен 7 и расположен в строке с искусственной базисной переменной , значит, она выходит из базиса.

Элементы второй симплекс-таблицы находятся обычными преобразованиями, элементы каждой из двух индексных строк находятся по правилу перпендикуляров. Базис во второй симплекс-таблице не содержит искусственной переменной, поэтому из дальнейшего рассмотрения столбец исключаем. Об оптимальности плана судим по второй индексной строке. Она содержит отрицательные элементы, следовательно, план Х₂ не оптимален. Ключевой столбец плана Х₂ соответствует столбцу , ключевой элемент находится в строке , следовательно, искусственная переменная из базиса уходит, и соответствующий ей столбец из рассмотрения исключаем. Переходим к плану .

Вторая индексная строка плана , нулевая, об оптимальности плана судим по первой индексной строке, все элементы которой оказались неотрицательны. Следовательно, план оптимален (табл. 6).

План оптимален, , . Окончательное решение исходной задачи: X^*=(42/5;0;8/5), F(X^*)=58/5.

Таблица 6.

		0	-1	-3	-2	0	0	-М	‑M
	Баз.	св.
-М		28	2	6	7	-1	0	1	0
0		36	2	4	5	0	1	0	0
-М		10	1	1	1	0	0	0	1
	W	0	1	3	2	0	0	0	0
	M	-38	-3	-7	-8	1	0	0	0
		4	2/7	6/7	1	-1/7	0	1/7	0
		16	4/7	-2/7	0	5/7	1		0
		6	5/7	1/7	0	1/7	0		1
	W	-8	3/7	9/7	0	2/7	0		0
	M	-6	-5/7	-1/7	0	-1/7	0		0
	x3	8/5
		56/5
		42/5	1	1/5	0	1/5	0
	W	-58/5	0	6/5	0	1/5	0
	M	0	0	0	0	0	0

При кормлении животных необходимо использовать корма вида А и С составит в количестве 42/5 и 8/5 кг, корм вида В вводить в рацион нецелесообразно. При этом минимальная стоимость суточного рациона составит 58/5 денежных единиц.