2.12. Понятие двойственности для симметричных задач линейного программирования

Рассмотрим понятие двойственности на примере задачи о рациональном использовании сырья.

Пусть на некотором предприятии решили рационально использовать отходы основного производства. В плановый период появились отходы m-видов в объемах единиц (. Из этих отходов, учитывая специфику предприятия, можно наладить производствоn-видов неосновной продукции.

Обозначим через норму расходов сырьяi-вида на единицу j-ой продукции. - цена единицыj- продукции. Неизвестные величины задачи: - объемы выпускаj-продукции, обеспечивающие предприятию максимальную выручку.

Математическая модель задачи:

, (1)

при ограничениях

(),

, ().

Предположим с самого начала, при изучении вопроса об использовании отходов основного производства на предприятии, появилась возможность реализации их некоторой организации. Необходимо установить цены на эти отходы. Обозначим цены через . Цены должны быть установлены исходя из двух основных условий: 1) общую стоимость сырья покупающая сторона стремится минимизировать; 2) предприятие согласно уступить свою продукции только по таким ценам, при которых оно получит за них выручку не меньшую той, что оно могло бы получить организовав собственное производство.

Математическая модель полученной задачи:

(2)

Переменные называются двойственными оценками (теневые цены).

Задачи (1) и (2) называются парой взаимодвойственных задач. Так как они написаны в симметричной форме их называют парой взаимодвойственных симметричных задач.

, при (), ()

при () ()

Сравнивая прямую и двойственную задачи можно установить следующие взаимосвязи:

1. Если прямая задача на максимум, то двойственная на минимум.

2. Коэффициенты целевой функции прямой задачи являются свободными членами ограничений двойственной задачи.

3. Свободные члены ограничений прямой задачи, являются коэффициентами целевой функции двойственной задачи.

4. Матрицы ограничений прямой и двойственной задачи являются транспонируемыми друг к другу.

5. Если прямая задача на максимум то ее система ограничений представляется в неравенства типа . Двойственная задача решается на минимум и знак.

6. Число ограничений прямой задачи равно числу переменных двойственной, а число ограничений двойственной равно числу переменных прямой.

7. Все переменные в обоих задачах не отрицательны.

Пример: Составить симметричную двойственную задачу:

при

Решение:

Исходная задача на максимум, значит двойственная – на минимум. Свободные члены системы ограничений исходной задачи равны 2 и 5. Значит коэффициенты в целевой функции двойственной задачи будут 2 и 5. Коэффициенты в целевой функции прямой задачи – 27, 10, 15, 28. Следовательно эти значения будут свободными членами в системе ограничений двойственной задачи. Таким образом, транспонируя матрицу А, получим:

при

Блок 3

3.1. Несимметричные двойственные задачи

Пуст ЗЛП задана в каноническом виде:

при

(),

().

Переведем данную задачу в симметричную форму:

Прямая задача на максимум, значит неравенства должны быть ≤. Умножим второе неравенство на (-1). Получим:

Составим двойственную задачу для полученной симметричной. Для этого введем двойственные переменные и. Получим:

при ограничениях:

Преобразуем систему ограничений следующим образом:

Обозначим y разность . иположительны, но их разность может быть как положительна, так и отрицательна.

В результате получим двойственную задачу вида:

при

Подводя итоги вышеизложенному, опишем прямую и двойственную задачу для ЗЛП в общем случае:

при (), (), (), –любого знака ().

при (), (), (), –любого знака ().

Таким образом, двойственная задача со смешанными ограничениями составляется с соблюдением следующих дополнительных правил:

1. Если на переменную прямой задачи наложено условие неотрицательности, тоj-тое условие системы ограничений двойственной задачи в виде неравенств и наоборот.

2. Если на переменную прямой задачи не наложено условие неотрицательности, тоj-тое ограничение двойственной задачи записывается в виде строго равенства.

3. Если в прямой задачи имеются ограничения равенства, то на соответствующие переменные двойственной задачи не налагается условие неотрицительности.

Задача двойственная двойственной будет совпадать с исходной. Поэтому безразлично которую задачу можно принять за прямую, которую за двойственную. Следует говорить о паре взаимно двойственных задач.

Рассмотри пару двойственных задач.

Теорема 1: (об основном неравенстве двойственности) Для любых допустимых планов X=иY=прямой и двойственной задачи линейного программирования справедливо неравенство:

.

Экономическое содержание основного неравенства двойственности состоит в том, что для любого допустимого плана производства Х и любого вектора оценок ресурсов Y общая созданная стоимость не превосходит суммарной оценки ресурсов.

Теорема 2: (критерий оптимальности Канторовича) Если для некоторых допустимых планов ипары двойственных задач выполняется равенствоz()=f(), тоиявляются оптимальными планами соответствующих задач.

Экономическое содержание теоремы состоит в том, что план производства Х и вектор оценок ресурсов Y является оптимальным, если цена всей произведенной продукции и суммарная оценка ресурсов совпадают.

Теорема 3: (малая теорема двойственности) Для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование допустимого плана для каждой из них.

Теорема 4: Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций равны: z()=f(). Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых планов, то система ограничений другой – противоречива.

Между переменными двойственных задач можно установить соответствие, сопоставляя свободным переменным одной задачи базисные переменные другой. Опорному оптимальному плану исходной задачи соответствует опорный оптимальный план двойственной, который оказывается записанным с противоположными знаками в индексной строке последней симплексной таблицы.

Пример 1: Решить исходную задачу линейного программирования, исходя из решения двойственной:

при

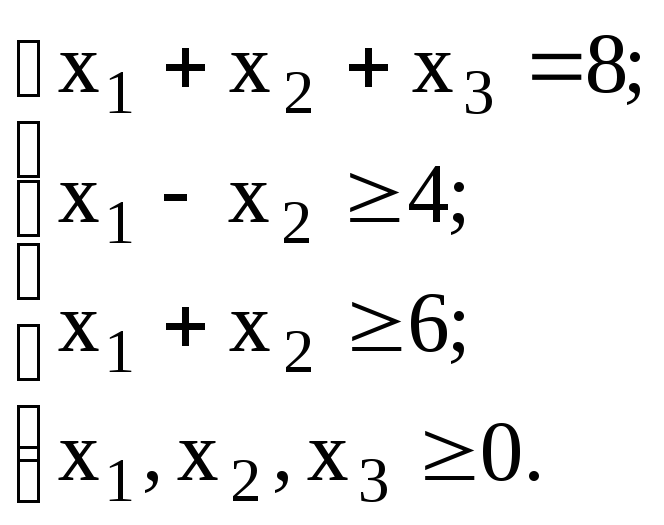
Решение.

Преобразуем систему ограничений следующим образом:

Составим двойственную задачу для данной:

при

Решим полученную задачу симплексным методом. Преобразуем систему ограничений следующим образом:

Для полученной М-задачи составим симплексную таблицу.

БП	СБ	А
			8	-4	-6	0	0	0	M	M	M
	M	1	1	-1	-1	-1	0	0	1	0	0
	M	1	1	1	-1	0	-1	0	0	1	0
	M	2	1	0	0	0	0	-1	0	0	1
M		4	3	0	0	-1	-1	-1	0	0	0
св. член		0	-8	4	6	0	0	0	0	0	0
	8	1	1	-1	-1	-1	0	0		0	0
	M	0	0	2	0	1	-1	0		1	0
	M	1	0	1	1	1	0	-1		0	1
M		1	0	3	1	2	-1	-1		0	0
св. член		8	0	-4	-2	-8	0	0		0	0
	8	1	1	0	-1	-1/2	-1/2	0			0
	-4	0	0	1	0	1/2	-1/2	0			0
	M	1	0	0	1	1/2	1/2	-1			1
M		1	0	0	1	1/2	1/2	-1			0
св. член		8	0	0	-2	-6	2	0			0
	8	2	1	0	0	0	0	-1
	-4	0	0	1	0	1/2	-1/2	0
	-6	1	0	0	1	1/2	1/2	-1
		10	0	0	0	-5	-1	-2

Полученный план оптимальный.

f=10 в (2, 0, 1, 0, 0, 0, 0)

Найдем решение прямой задачи.

Z=10 в (5, 1, 2)