3.10. Задача выпуклого программирования

Определение 1: Функция f(x), определенная на выпуклом множестве Х, называется выпуклой, если для любых точек ииз этого множества и любогосправедливо неравенство:

.

Если в этом соотношении при и любыхиХ (≠) имеет место строгое неравенство, тоf(x) называется строго выпуклой.

Определение 2: Функция f(x), определенная на выпуклом множестве Х, называется вогнутой, если для любых точек ииз этого множества и любогосправедливо неравенство:

.

Если в этом соотношении при и любыхиХ (≠) имеет место строгое неравенство, тоf(x) называется строго вогнутой.

Определение 3: Задача математического программирования

при ограничениях

(),

().

в которой либо целевая функция, либо ограничения, либо то и другое нелинейны, называется нелинейной.

Класс задач нелинейного математического программирования очень велик. Общих универсальных методов нет. Однако, есть задачи нелинейного программирования, для которых есть методы решения. Один из таких типов задач являются задачи выпуклого программирования.

В теории выпуклого программирования в качестве основной обычно рассматривается задача минимизации выпуклой функции n переменных при ограничениях(), (), где функции предполагаются выпуклыми.

Если иявляются вогнутыми, то имеем задачу максимизациипри ограничениях(), ().

3.11. Метод множителей Лагранжа

Метод множителей Лагранжа является классическим методом решения задач математического программирования (в частности выпуклого).

Рассмотрим классическую задачу оптимизации

при ограничениях

().

От основной задачи выпуклого программирования в данной постановке задача отличается тем, что в системе ограничений нет неравенств и нет ограничения неотрицательности для переменных.

Классический подход к решению данной задачи дает систему уравнений (необходимые условия), которым должна удовлетворять точка , доставляющая функциилокальный экстремум на множестве точек, удовлетворяющих системе ограничений (для задачи выпуклого программирования найденная точка будет и глобальным экстремум).

Предположим, что в точке функцияимеет локальный условный экстремум и ранг матрицы

равен m. Тогда необходимые условия запишутся в виде:

(),

(),

где

есть функция Лагранжа, – множители Лагранжа.

Алгоритм решения задачи методом множителей Лагранжа:

1. Составить функцию Лагранжа.

2. Найти частные производные функции Лагранжа по всем переменным и приравнять их к нулю. Получим систему изn+m уравнений с n+m неизвестными. Решив полученную систему, вычислим стационарные токи функции Лагранжа.

3. Из стационарных точек, взятых без 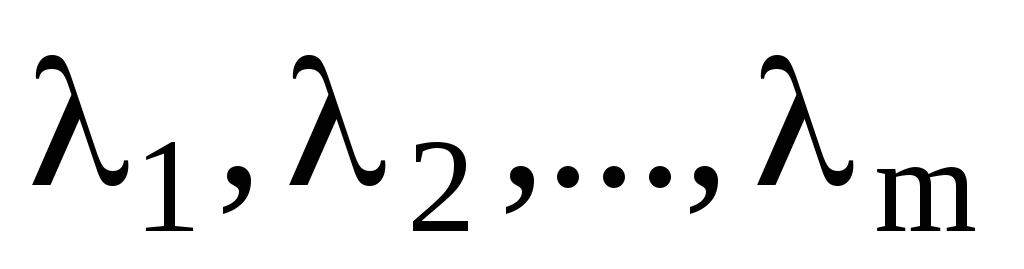, выбрать точки, в которых функция имеет условный локальный экстремумы при наличии ограничений.

Пример: Решить задачу математического программирования, используя метод множителей Лагранжа.

при

,

Решение:

Будем решать задачу без учета неотрицательности переменных.

1. Составим функцию Лагранжа.

2. Найдем ее частные производные по .

Приравняв производные к нулю, получим систему:

Решим ее:

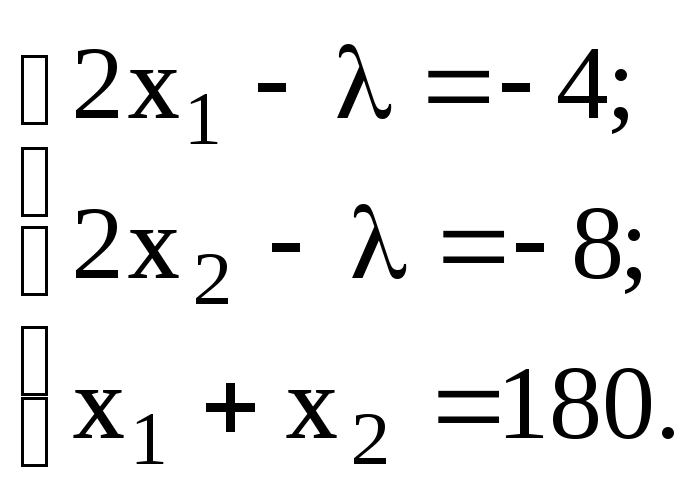
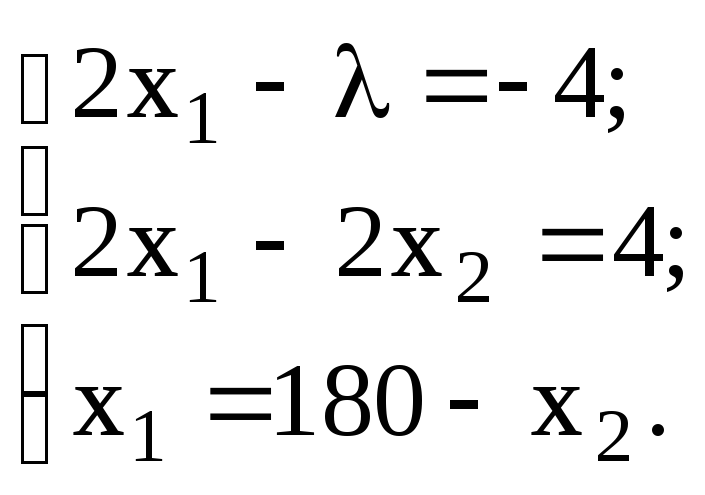
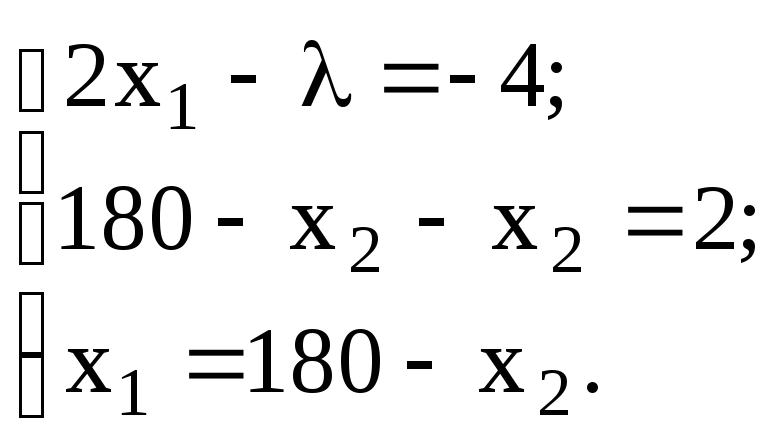
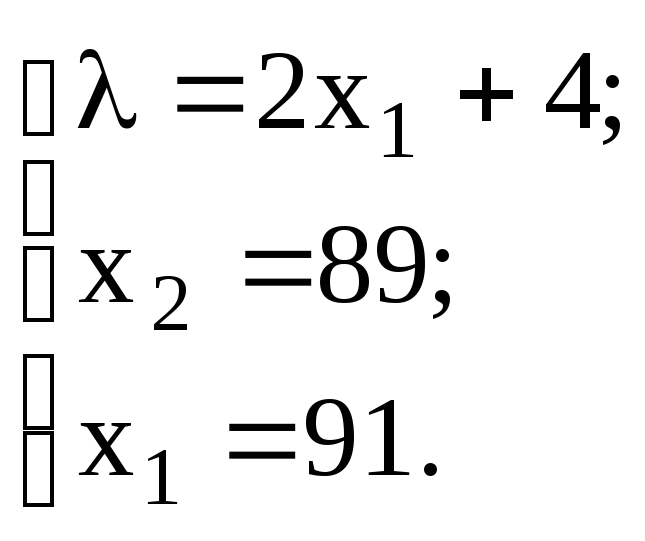
Получена стационарная точка (91, 89). С помощью вторых производных легко доказать, что в полученной точке функция достигает условный локальный экстремум. Данная точка является точкой минимума функции.

Ответ: Z=17278.