Окончание табл. 2.1
9	(3; 5)	(11; 1)	(6; 5)
10	(3; –4)	(12; –6)	(8; –4)
11	(4; –3)	(12; –5)	(7; –3)
12	(5; –1)	(14; –3)	(8; –1)
13	(–5; 0)	(4; –2)	(2; 0)
14	(–4; 1)	(5; –2)	(3; 1)
15	(–3; 2)	(6; –2)	(2; 2)
16	(–2; 4)	(7; 0)	(5; 4)
17	(–3; 3)	(6; –1)	(4; 3)
18	(–3; 0)	(6; –2)	(2; 0)
19	(–2; 5)	(7; 1)	(4; 5)
20	(–1; 1)	(8; –3)	(4; 1)
21	(–2; 4)	(7; 0)	(5; 4)
22	(1; 6)	(10; 2)	(7; 6)
23	(2; 4)	(10; 1)	(6; 4)
24	(2; 5)	(11; 3)	(7; 5)
25	(0; 4)	(9; 0)	(7; 4)
26	(1; 5)	(10; 2)	(3; 5)
27	(–4; 4)	(5; 1)	(2; 4)
28	(–4; 5)	(5; 1)	(3; 5)
29	(–3; 1)	(6; –3)	(3; 1)
30	(0; 6)	(9; 3)	(6; 6)

28

ТЕМА 3

КРИВЫЕ ВТОРОГО ПОРЯДКА

Линии на плоскости, которые описываются уравнениями вида

Ax2 + Bxy +Cy2 + Dx + Ey + F = 0 ,

(1.23)

где коэффициенты A, B,C не равны нулю одновременно ( A2 + B2 +C2 ≠ 0 ), на-

зываются линиями второго порядка.

К линиям второго порядка относятся окружность, эллипс, гипербола, па-

рабола.

Окружность – геометрическое место точек равноудаленных от одной точки, называемой центром окружности.

Каноническое уравнение окружности с центром в точке C(a,b) и радиусом, равным R имеет вид:

(x − a)2 + ( y −b)2 = R2 .

(1.24)

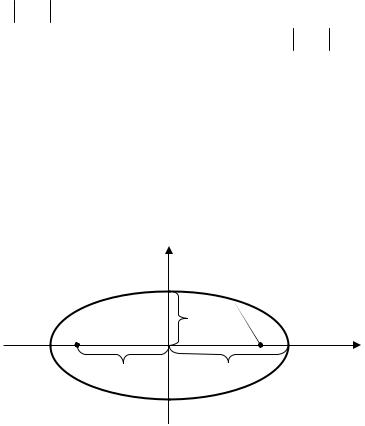
Эллипсом называется геометрическое место точек, сумма расстояний каждой из которых от двух данных точек F1 и F2 (фокусов) есть постоянная ве-

личина 2a , большая F1F2 .

Обозначим расстояние между фокусами 2c , т.е. F1F2 = 2c . Если фокусы

эллипса лежат на оси Ox так, что начало координат лежит в середине отрезка F1F2 . Тогда в выбранной системе координат точки F1 и F2 имеют соответст-

венно координаты (−c;0) и (c;0) и каноническое уравнение эллипса имеет вид

	х2	+	у2	=1,			(1.25)
	а2		b2
где b2 = a2 −c2 .
						у
						М(х; у)
					r1	b	r2
				F1	c	a	х
							F2

Рис. 1.10

29

Эллипс, заданный уравнением (1.25), симметричен относительно осей координат (рис.1.10). Отрезки длиной a и b называются соответственно большой

	и малой полуосями эллипса. Если a >b , то фокусы F1		и F2 находятся на оси
	Ox на расстоянии с = a2 −b2 от центра. Отношение	с	=ε <1 называется экс-
		а

центриситетом эллипса. Расстояния от произвольной точки M (x, y) эллипса до его фокусов (фокальные радиусы-векторы) определяются формулами

r1 = a −εx, r2 = a +εx .		(1.26)
Если a < b ,	то фокусы находятся на оси Oy	и имеют место равенства
с = b2 − a2 , ε = c	, r =b ±ε y .
b

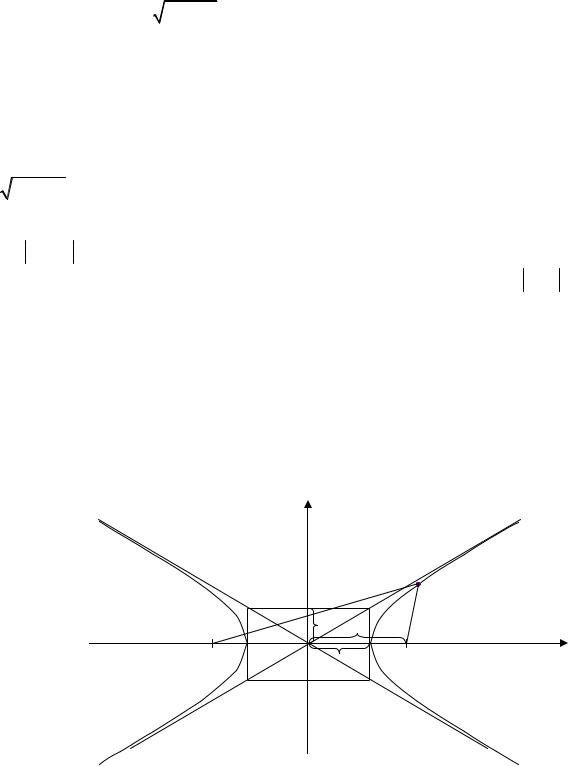
Гиперболой называется геометрическое место точек, для которых разность s1 − s2 расстояний s1 и s2 до двух заданных точек F1 и F2 , называемых

фокусами гиперболы, есть величина постоянная, равная 2a (0 < 2a < F1F2 = 2c) .

Если начало системы координат находится в середине отрезка и ось Ox направлена по прямой F1F2 , то точки F1 и F2 имеют соответственно координа-

ты (−c;0) и (c;0) . В этом случае каноническое уравнение гиперболы имеет вид

	х2	−	y2	=1	,	(1.27)
	a2		b2

где b2 = c2 − a2 .

y = − b x	y		y = b x
a			a
			M (x, y)
r1	b	c	r2	x
F1		a	F2

Рис. 1.11

30

Гипербола, заданная уравнением (1.27), симметрична относительно осей координат (рис. 1.11). Она пересекает ось Ox в точках A1(a,0) и A2 (−a,0) , на-

зываемых вершинами гиперболы и не пересекает ось Oy .

Отрезки a и b называются соответственно вещественной (действитель-

ной) и мнимой осями гиперболы. Параметр с =

a2 +b2 равен расстоянию от

центра до фокусов. Отношение

с

=ε >1 называется эксцентриситетом гипер-

а

болы. Прямые у = ± b

х называются асимптотами гиперболы. Расстояния от

a

произвольной точки

M (x, y) гиперболы до ее фокусов (фокальные радиусы-

векторы) определяются формулами:

r1 =

εx − a

,

r2 =

εx + a

.

(1.28)

Гипербола, у которой a =b ,

называется равносторонней, ее уравнение

x2 − y2 = a2 , а уравнение асимптот y = ±x .

Гиперболы

х2

−

y2

=1 и

у2

−

x2

=1 называют сопряженными.

a2

b2

b2

a2

Параболой называется геометрическое место точек на плоскости равноудаленных от заданной точки (фокуса параболы) и заданной прямой, называемой директрисой параболы.

Каноническое уравнение параболы

y2 = 2 px ,

если парабола симметрична относительно оси Ox (рис. 1.12) и

x2 = 2 py ,

если парабола симметрична относительно оси Oy .

	y
A		M
p	2 F (p	2 ;0)	x

Рис. 1.12

31