
матан 3 курс 2013 / практика / Невизначений інтеграл / практическое занятие № 3
.docМІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
ГОРЛІВСЬКИЙ ТЕХНІКУМ ДОНЕЦЬКОГО НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ
ПРАКТИЧНЕ ЗАНЯТТЯ № 3
з теми: «Інтегрування трансцендентних функцій.»
Модуль КЗН-02. ПР.О.03.07 Невизначений інтеграл.
Дисципліна: «Математичний аналіз»
|
Розглянуто та схвалено на засіданні циклової комісії інформаційних технологій та прикладної математики
протокол № ____ від _______20__ р.
Голова циклової комісії ПМ О.В. Велікодна
|
Розробив викладач Велікодна О. В.
|
ПЛАН ЗАНЯТТЯ
Дата: курс: ІІI
Викладач: Велікодна Ольга Володимирівна.
Тема: Інтегрування трансцендентних функцій.
Мета:
-
Дидактична: напрацювати вміння обчислювати первісну, застосовувати основні методи інтегрування, знаходити первісну раціональних функцій, трансцендентних та ірраціональних функцій.
-
Виховна: розвивати логічне мислення, усне мовлення студентів.
-
Методична: вдосконалювати методику проведення практичних занять з використанням технології проблемного та проектного навчання.
Тип: практичне заняття
Вид: практичне заняття – дослідження.
Методи та форми проведення заняття: практичні, дедуктивні, проблемно – пошукові, фронтальна, групова робота.
Наочні посібники: -
Роздавальний матеріал: тестові завдання до актуалізації знань, картки - завдання до самостійного виконання студентами.
Обчислювальні засоби: -
Література:
-
Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.
-
Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.
-
Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.
-
Марон А. И. Дифференциальное и интегральное исчисление функции одной переменной в примерах и задачах. – М.: Наука, 1973.
ХІД ЗАНЯТТЯ
-
Організаційна частина:
-
відсутні;
-
підготовка до заняття;
-
перевірка д/з.
-
Мотивація навчальної діяльності студентів: вивчити основний математичний апарат – невизначений інтеграл, що дає змогу розв’язувати прикладні задачі в різних галузях науки та техніки.
-
Актуалізація опорних знань: методи інтегрування трансцендентних функцій
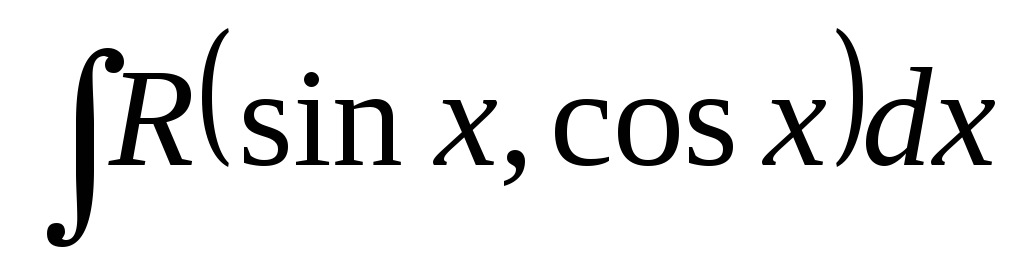 ,
,
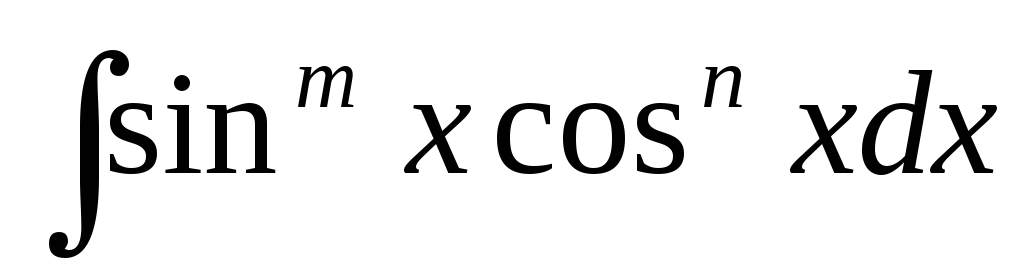 ,
,
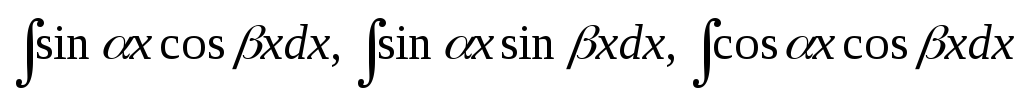 ,
,
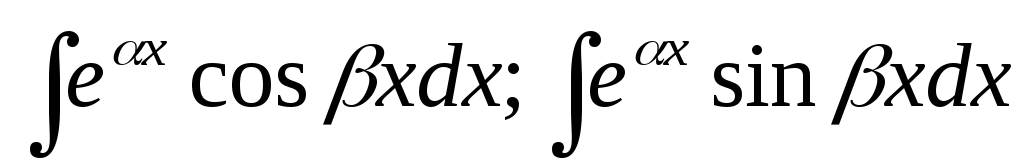 ,
,
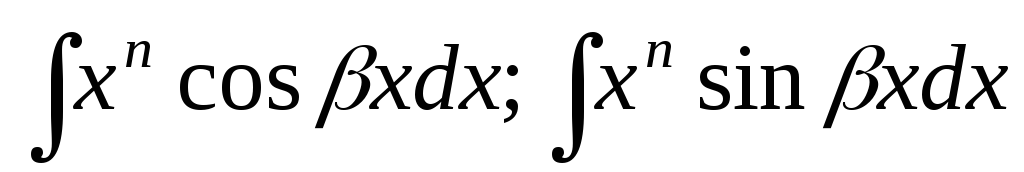 ,
,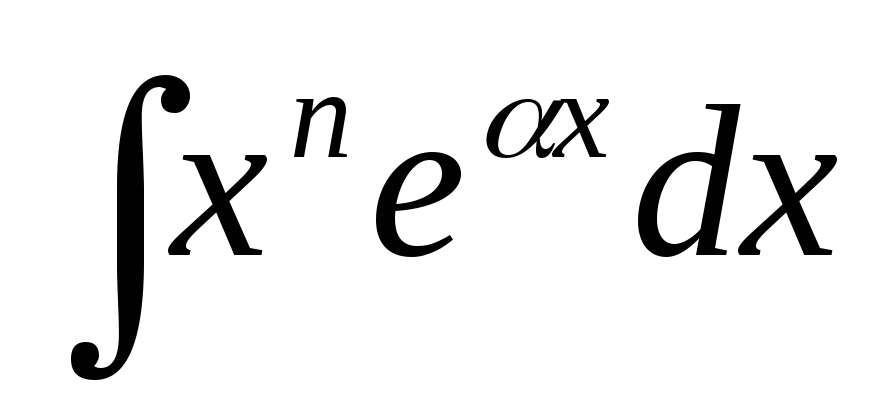 ,
,
 ;
;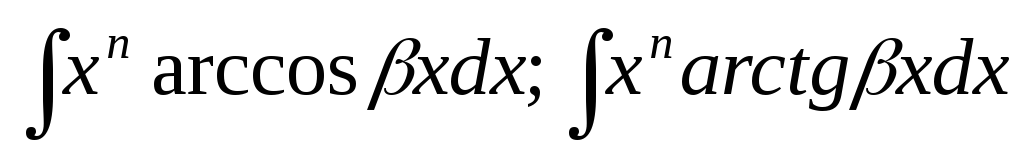 ;
;
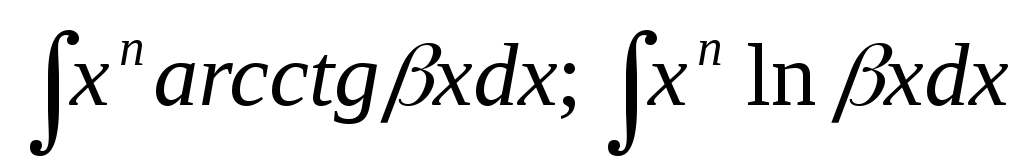 ,
,
-
Контроль за підготовкою студентів до практичного заняття:
-
Інструктаж щодо виконання практичної роботи.
-
Видача завдань для виконання роботи.
-
Виконання студентами практичної роботи.
-
Оформлення індивідуальних звітів виконаної роботи, захист практичної роботи.
-
Підведення підсумків. Оцінювання.
-
Домашнє завдання:
Конспект практичного заняття № 3.
Тема: «Інтегрування трансцендентних функцій.»
-
Інструктаж до виконання практичного завдання.
Методичні вказівки.
Інтеграли виду
![]() зводиться підстановкою
зводиться підстановкою
![]() до інтегралу від раціональної функції.
Користуючись формулами універсальної
підстановки, маємо:
до інтегралу від раціональної функції.
Користуючись формулами універсальної
підстановки, маємо:
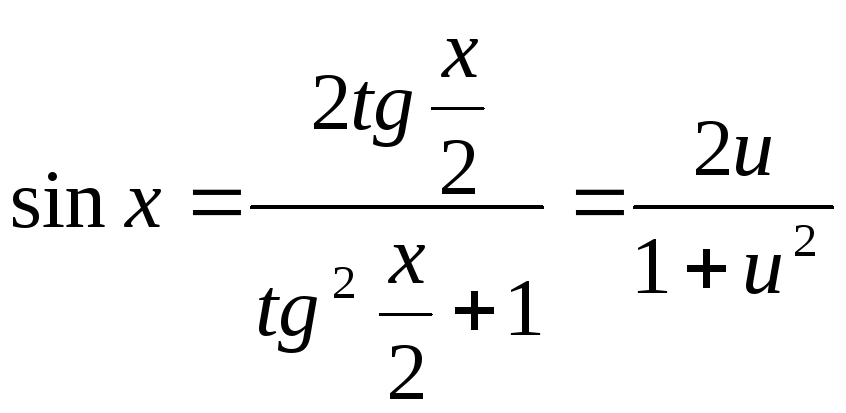 ,
,
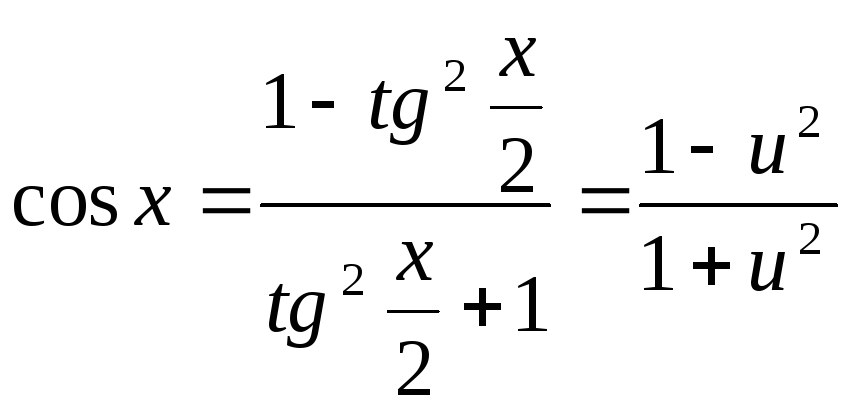 .
Тоді маємо:
.
Тоді маємо:
![]() .
Підставляючи отримані вирази в даний
інтеграл, маємо:
.
Підставляючи отримані вирази в даний
інтеграл, маємо:
![]() =
=
![]() ,
тобто отримали інтеграл від раціональної
функції. Також при обчисленні інтегралів
типу
,
тобто отримали інтеграл від раціональної
функції. Також при обчисленні інтегралів
типу
![]() часто доцільно використовувати
підстановки
часто доцільно використовувати
підстановки
![]() .
.
Інтеграли виду
![]() обчислюються в залежності від ступенів
n та m. Розглянемо можливі випадки.
обчислюються в залежності від ступенів
n та m. Розглянемо можливі випадки.
-
n та m – раціональні числа. Тоді підстановкою
 чи
чи
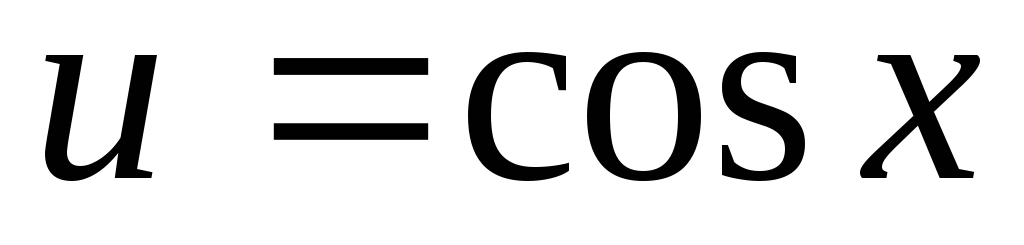 інтеграл
інтеграл
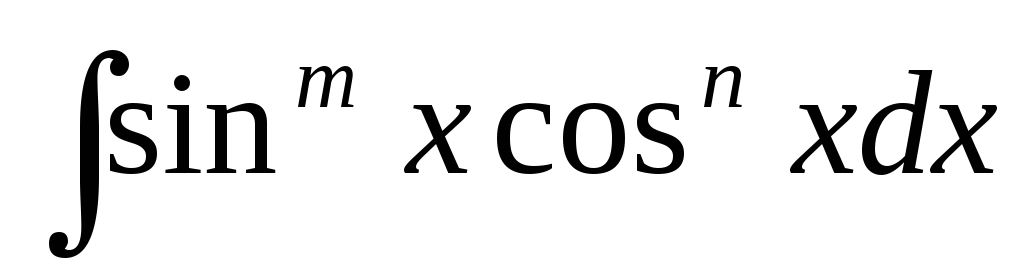 зводиться до виду інтеграла від
диференційного біному. Дійсно, якщо
зводиться до виду інтеграла від
диференційного біному. Дійсно, якщо
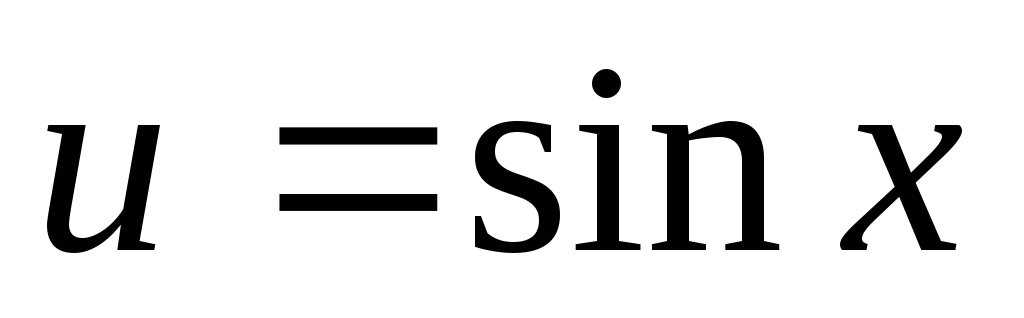 ,
то
,
то
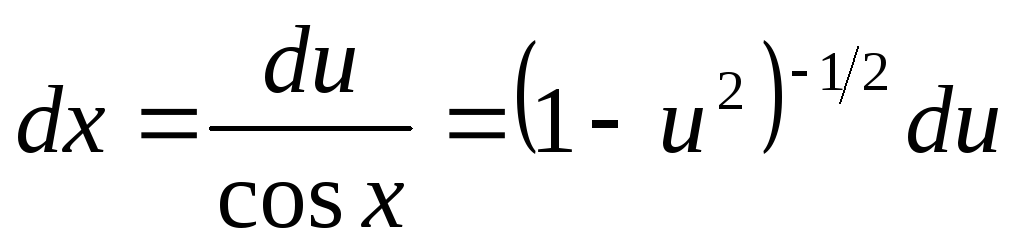 .
Тоді
.
Тоді
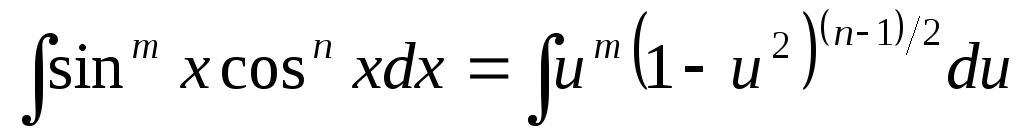 .
. -
якщо n та m – цілі числа, причому n – парне, m – непарне, то вводимо заміну
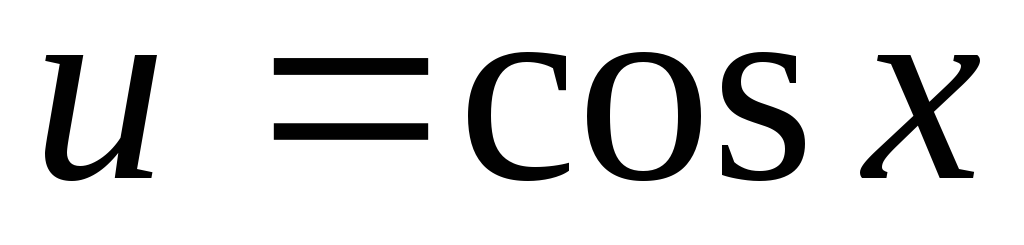 та використовуємо основну тригонометричну
тотожність
та використовуємо основну тригонометричну
тотожність
 .
Дійсно, маємо
.
Дійсно, маємо
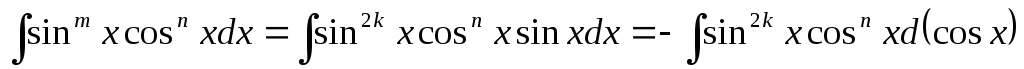 =
=
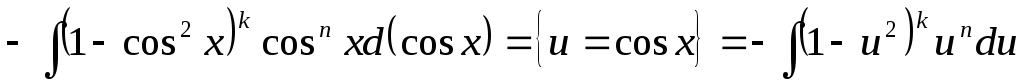 .
Таким чином, отримали інтеграл від
раціональної функції.
.
Таким чином, отримали інтеграл від
раціональної функції. -
якщо n та m – цілі числа, причому n – непарне, m –парне, то вводимо заміну
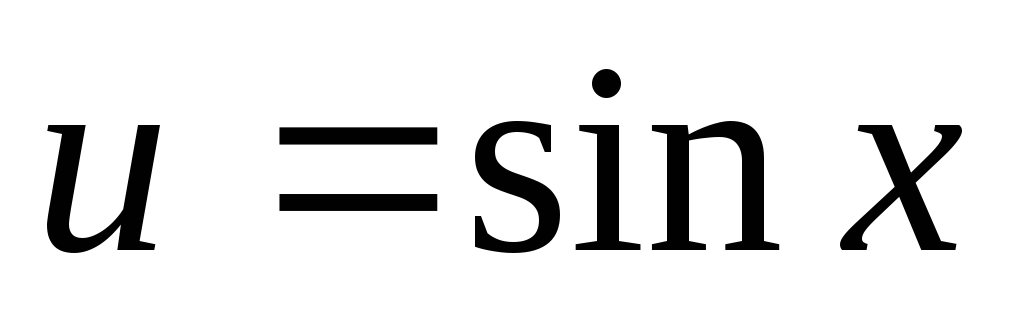 та використовуємо основну тригонометричну
тотожність
та використовуємо основну тригонометричну
тотожність
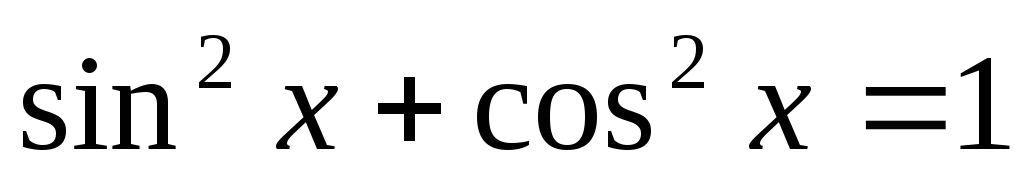 .
Дійсно, маємо
.
Дійсно, маємо
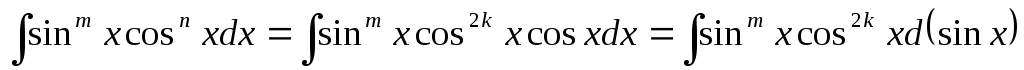 =
=
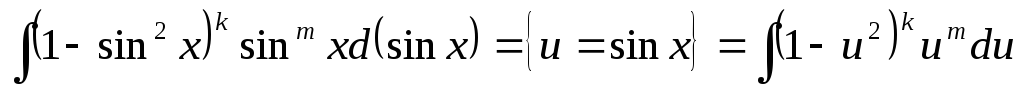 .
Таким чином, отримали інтеграл від
раціональної функції.
.
Таким чином, отримали інтеграл від
раціональної функції. -
якщо n та m – цілі числа, причому n – непарне, m –непарне, тобто n = 2k + 1, m = 2l + 1, то вводимо заміну
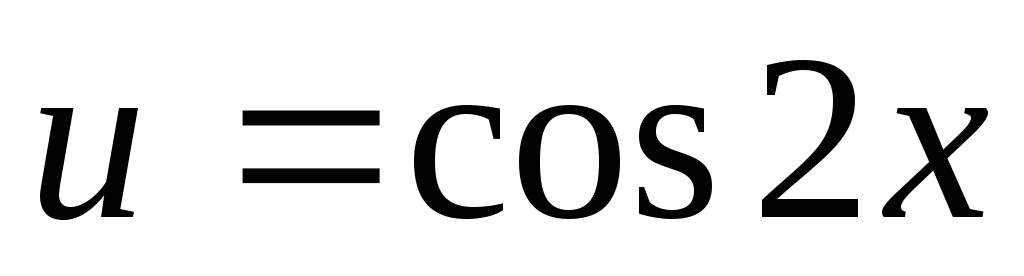 . Дійсно,
. Дійсно,
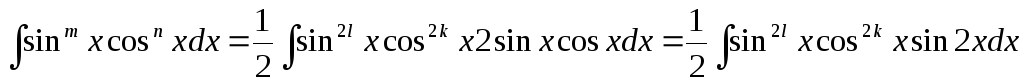 =
= Таким чином, отримали інтеграл від
раціональної функції(k та l можуть бути
від’ємними).
Таким чином, отримали інтеграл від
раціональної функції(k та l можуть бути
від’ємними). -
якщо n та m – цілі числа, причому n –парне, m –парне, тобто n = 2k, m = 2l, то вводимо заміну
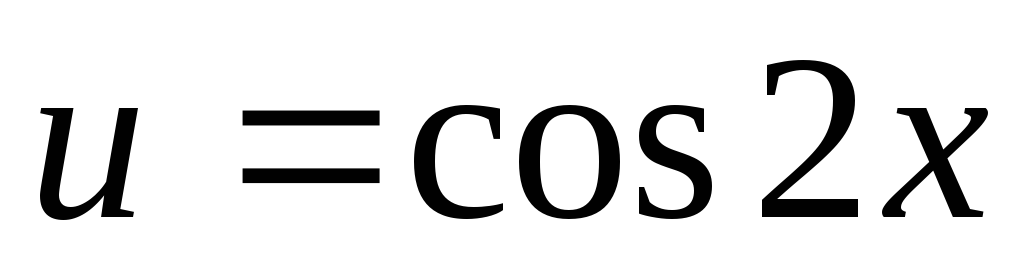 чи заміну
чи заміну
 ,
та користуємось формулами зниження
ступеня:
,
та користуємось формулами зниження
ступеня:
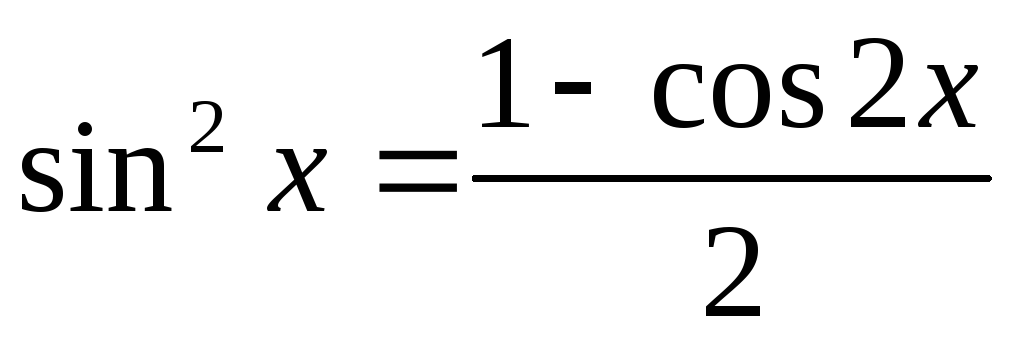 ,
,
 .
При цьому отримаємо інтеграл того ж
типу, але від функцій нижчого ступеня.
.
При цьому отримаємо інтеграл того ж
типу, але від функцій нижчого ступеня.
Інтеграли виду
![]() обчислюються, якщо їх підінтегральні
вирази спростити за формулами:
обчислюються, якщо їх підінтегральні
вирази спростити за формулами:
![]() ;
;
![]() ;
;
![]() .
.
Для обчислення інтегралів
![]() потрібно двічі про інтегрувати їх за
частинами – в результаті отримаємо для
них лінійне рівняння, з якого відразу
знайдуться інтеграли.
потрібно двічі про інтегрувати їх за
частинами – в результаті отримаємо для
них лінійне рівняння, з якого відразу
знайдуться інтеграли.
В інтегралах
![]() ;
;![]() після однократного інтегрування за
частинами отримаємо інтеграли того ж
типу, але з меншим показником ступеня.
після однократного інтегрування за
частинами отримаємо інтеграли того ж
типу, але з меншим показником ступеня.
В інтегралах
![]() ;
;![]() ;
;
![]() після однократного інтегрування за
частинами пропаде трансцендентна
функція, причому в інтегралах
після однократного інтегрування за
частинами пропаде трансцендентна
функція, причому в інтегралах
![]() ;
;![]() отримаємо інтеграл від ірраціональної
функції, що виражається через елементарні
функції, а в інтегралах
отримаємо інтеграл від ірраціональної
функції, що виражається через елементарні
функції, а в інтегралах
![]() ;
;![]() - інтеграл від раціональної функції, що
виражається через елементарні функції.
- інтеграл від раціональної функції, що
виражається через елементарні функції.
Приклади виконання практичного завдання.
-
Знайти інтеграл
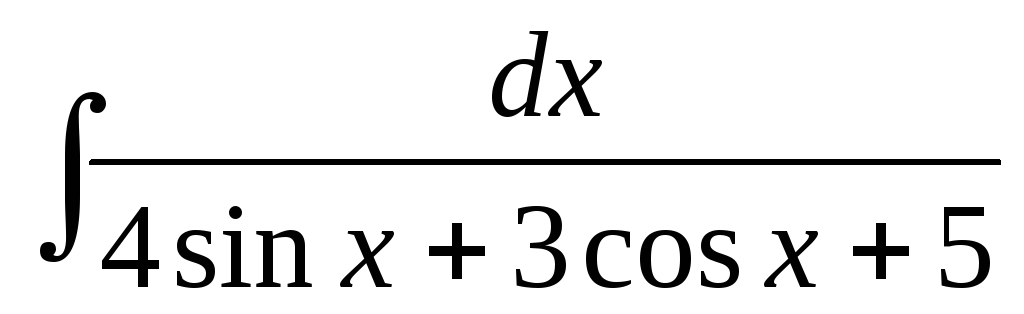 .
.
Підінтегральна
функція залежить раціонально від
тригонометричних функцій, тому
застосовуємо підстановку
![]() .
Тоді маємо:
.
Тоді маємо:
![]() ,
,
![]() ,
,
![]() .
.
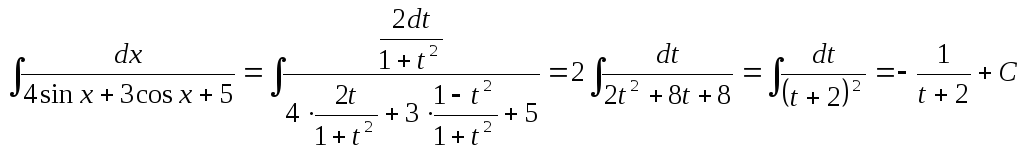 .
.
Звертаючись
до старої змінної, отримаємо:
 .
.
-
Знайти інтеграл
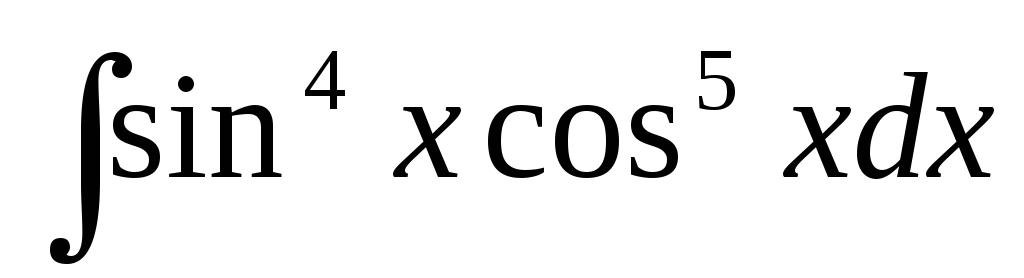 .
.
Застосовуємо
заміну:
![]() .
.
![]() =
=
=
![]()
![]() .
.
-
Знайти інтеграл
 .
.
![]() =
=
=
![]() =
=
=
=![]() =
=
=![]() .
.
-
Виконати практичне завдання.
Знайти інтеграл.
1.![]() 2.
2.![]()
3.![]() 4.
4.![]()
5.![]() 6.
6.![]()
7.![]() 8.
8.![]()
9.![]() 10.
10.![]()
11.![]() 12.
12.
![]()
13.![]() 14.
14.![]()
15.![]() 16.
16.![]()
17.![]() 18.
18.![]()
19.![]() 20.
20.![]()
21.![]() 22.
22.
23.![]() 24.
24.![]()
25.![]()
-
Домашнє завдання.
Б. П. Демидович. Сборник задач и упражнений по математическому анализу.
Стор. 193, №№1991 – 2010.
Стор. 195, №№2025 – 2027, 2034 – 2037.
