матан 3 курс 2013 / лекции / Функціональні послідовності і ряди / лекция № 24

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

ГОРЛІВСЬКИЙ ТЕХНІКУМ ДОНЕЦЬКОГО НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ

ЛЕКЦІЯ № 24

з теми: «Збіжність функціональних послідовностей і рядів. Рівномірна збіжність.»

Модуль КЗН-02.ПР.О.03.11 Функціональні послідовності і ряди

Дисципліна: «Математичний аналіз»

Розглянуто та схвалено на засіданні циклової комісії інформаційних технологій та прикладної математики. Протокол № ____ від _______20__ р. Голова циклової комісії ПМ Велікодна О. В.

Розробив викладач Велікодна О. В.

ПЛАН ЗАНЯТТЯ

Дата: курс: ІІІ

Викладач: Велікодна Ольга Володимирівна.

Тема: Збіжність функціональних послідовностей і рядів. Рівномірна збіжність.

Мета:

• Дидактична: розглянути поняття функціональної послідовності та функціонального ряду, ознайомитися з поняттями збіжності та рівномірної збіжності функціональних послідовностей та рядів.

• Виховна: виховувати професійно спрямовану особистість, здатну чітко та логічно висловлювати та доводити свої думки.

• Методична: вдосконалювати методику проведення лекції з використанням методики проектної технології.

Тип: лекція

Вид: лекція з використанням проектної технології.

Методи та форми проведення заняття: мовні, пояснювально-ілюстративні, проблемно-пошукові, наочні.

Науково-методичне забезпечення:

1. Кудрявцев Л.Д. Курс математического анализа: Учебник. Для студентов университетов и вузов. В 3 т. - М.: Высшая школа,1998.

2. Кудрявцев Л.Д. Сборник задач по математическому анализу: Учебник для вузов. В 3 т. - М.: Наука. Гл. ред. физ. - мат. лит.,1989.

3. Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для вузов. - М.: Наука. Гл. ред. физ. - мат. лит.,1975.

Між предметні зв’язки:

• Дисципліни, що забезпечують: елементарна математика

• Дисципліни, що забезпечуються: лінійна алгебра та аналітична геометрія, дискретна математика, диференціальні рівняння, рівняння математичної фізики, чисельні методи, методи оптимізації, теорія функцій комплексної змінної.

Обладнання: зошити, ручки, крейда, дошка.

ХІД ЗАНЯТТЯ

1. Організаційна частина:

1. відсутні;

2. підготовка до заняття;

3. перевірка д/з.

2. Актуалізація опорних знань: визначення числового ряду, часткових сум числового ряду, суми числового ряду, визначення збіжного та розбіжного числових рядів, необхідна умова збіжності числового ряду, властивості збіжного числового ряду, критерій Коші збіжності числового ряду, приклади збіжних та розбіжних числових рядів, достатні умови збіжності знакододатних числових рядів (ознаки збіжності інтегральна, зрівняння, Д’Аламбера, Коші), визначення знакозмінних числових рядів, визначення абсолютно збіжних та умовно збіжних числових рядів, ознаки збіжності для абсолютно збіжних числових рядів, ознака Лейбніца для знакочергуючого ряду, ознаки Абеля та Дирихлє для довільних числових рядів, Теорема Рімана про підсумовування умовно збіжних числових рядів. Визначення функції; основні елементарні функції та їх властивості.

3. Вивчення нового матеріалу:

• Тема лекції: Збіжність функціональних послідовностей і рядів. Рівномірна збіжність.

• Мотивація вивчення матеріалу: вивчити основні методи дослідження функціональних рядів для подальшого їх застосування як при розв’язанні математичних, так і прикладних задач.

• План вивчення нового матеріалу: надається в конспекті лекції.

4. Виклад нового матеріалу. Конспект лекції надається.

5. Закріплення нового матеріалу.

6. Підсумки заняття.

7. Домашнє завдання:

Конспект лекції № 24.

Тема: Збіжність функціональних послідовностей і рядів. Рівномірна збіжність.

План лекції № 24.

1. Збіжність функціональних послідовностей й рядів.

2. Рівномірна збіжність функціональних послідовностей та рядів.

Нехай на деякій множині Х будь-якої природи задана послідовність функцій , що приймають числові значення. Елементи множини Х будемо називати точками.

Визначення 1. Послідовність називається обмеженою на множині Х, якщо існує таке число c > 0, що для всіх n = 1, 2, .... та всіх точок виконується нерівність .

Визначення 2. Послідовність називається збіжною на множині Х, якщо при будь-якому фіксованому числова послідовність збігається.

Визначення 3. Якщо послідовність збігається на множині Х, то функція ƒ, визначена при кожному рівністю називається границею послідовності .

Нехай на множині Х задана послідовність числових функцій .

Визначення 4. Множина всіх числових рядів , в кожному з яких точка вільно фіксована, називається рядом на множині Х, а функції - його членами.

Аналогічно числовим рядам сума називається частковою сумою ряду n-го порядку, а ряд - його n-м залишком.

Визначення 5. Ряд називається збіжним на множині Х, якщо послідовність його часткових сум збігається на цій множині. Границя часткових сум називається сумою ряду , тобто та функція s(х) розкладається в ряд .

Якщо ряд при будь-якому фіксованому збігається абсолютно, то він називається абсолютно збіжним на множині Х.

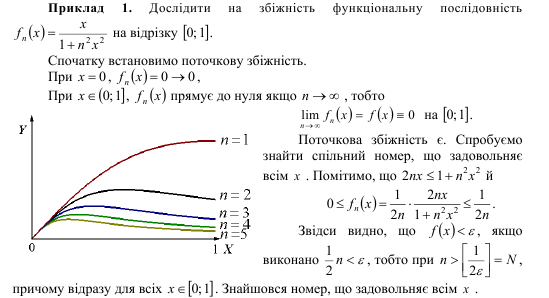
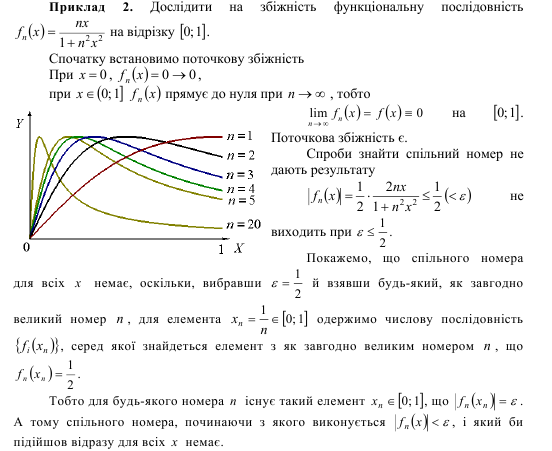
Визначення 6. Функціональна послідовність називається рівномірно збіжною до функції ƒ на множині Х, якщо для будь-якого існує такий номер , що для всіх точок та всіх номерів має місце нерівність . Якщо послідовність збігається на множині Х до функції ƒ, то пишуть , а якщо послідовність збігається рівномірно до функції ƒ на даній множині, то пишуть .

За допомогою символів визначення можна записати наступним чином:

Таким чином, якщо послідовність тільки просто збігається до функції ƒ на множині Х, то для кожної точки існує свій номер , для котрого при виконується н6ерівність , та може бути, що для всіх точок неможливо обрати загальний номер , що має вказані властивості.

Рівномірна збіжність послідовності до функції ƒ означає, що для будь-якого можна обрати такий номер , що в будь-якій точці виконується нерівність .

Теорема. Для того щоб послідовність рівномірно збігалась до функції ƒ на множині Х, необхідно та достатньо, щоб .

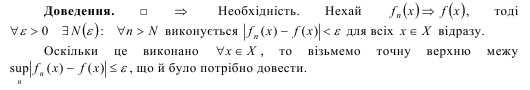
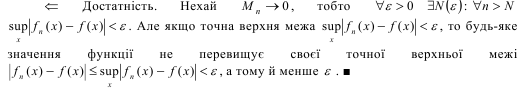
Наслідки. Якщо існує нескінченно мала послідовність , тобто , така, що для всіх виконується нерівність , то послідовність рівномірно збігається до функції ƒ на множині Х.

Теорема (Критерій Коші рівномірної збіжності функціональної послідовності). Для того, щоб послідовність рівномірно збігалась на множині Х до функції ƒ, необхідно та достатньо, щоб для будь-якого існував такий номер , що для всіх точок та всіх номерів та всіх р = 0, 1, 2, … мала місце нерівність .

За допомогою символів критерій можна записати наступним чином:

(доведення критерію розібрати самостійно).