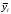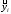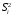4. Расчёт необходимого объёма выборки, т.Е. Репрезентативной (представительной) выборки (необходимого числа параллельных опытов)

Проведём расчёт необходимого объёма выборки, т.е. репрезентативной (представительной) выборки.

Коэффициент вариации:

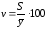
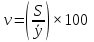, (4.1)

где     S – среднее квадратичное отклонение;

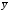
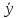– выборочное среднее.

v 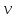= (37,455/467,844) ·100 = 8,01 %.

Определим объём репрезентативной выборки:

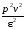
n_p = 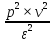, (4.2)

где     р – уровень достоверности (р = 1 – q = 1– 0,05 = 0,95);

ε – относительная допускаемая ошибка:

ε = 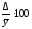%, (4.3)

где     Δ – абсолютная допускаемая ошибка:

Δ = 

а t= 2,00 для числа степеней свободы f = 60 – 1 = 59 и q = 0,05 по табл. 2 приложения, [2]. Отсюда

ε = (9,671/467,844)·100 = 2,07 %.

n_p =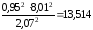≈ 14.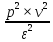

5. Обработка результатов эксперимента

5.1. Вычисляем среднее арифметическое выходных величин для каждой серии дублированных опытов, используя данные табл. 2.2:

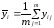, (5.1)

где m – число дублированных опытов в каждой серии. Для первой серии:

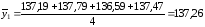м³/сут.

Аналогично вычисляются средние арифметические значения выходных величин для других серий. Результаты заносим в табл. 5.1.

Таблица 5.1

№ опыта
1	137,26	137,51	0,2596
2	157,72	157,89	0,2625
3	260,83	260,49	0,2625
4	320,42	320,11	0,2625
5	294,25	295,29	0,2625
6	372,40	373,31	0,2625
7	563,54	563,91	0,2625
8	755,10	755,49	0,2625

5.2. Вычисляем коэффициенты регрессии:

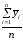
b₀ = , (5.2)

b_i =, (5.3)

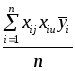
b_iu = .(5.4)

В частности, для свободного члена по формуле (5.2) получим:

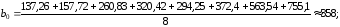
для коэффициента b₁ по формуле (5.3):

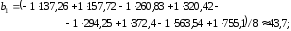
для коэффициента b₁₂ по формуле (5.4):

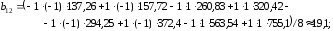
для коэффициента b₁₂₃ по формуле (5.4):

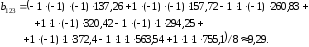
Проводя аналогичные вычисления по формулам (5.3) и (5.4) для других коэффициентов, получим следующие значения других коэффициентов регрессии:

b₂ =117; b₃ = 139; b₁₃ = 23,7; b₂₃ = 45,7.

5.3. Находим значение выходной величины по функции отклика:

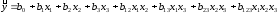, (5.5)

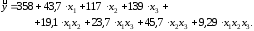
В частности, расчётное значение выходной величины для первой серии опытов:

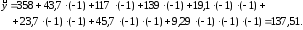
Аналогично вычисляются и значения выходной величины для других серий опытов, значения заносятся в таблицу 5.1.

5.4. Вычисляем оценки дисперсии:

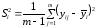, (5.6)

где     m – число дублированных опытов в каждой серии;

y_{i j} – значение выходной величины в j-м дублированном опыте i-ой серии. Для первой серии:

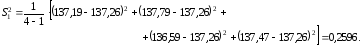
Аналогично проводятся расчёты для других серий. Результаты заносим в таблицу 5.1.

5.5. Проверяем однородность дисперсии опытов по критерию Кохрена:

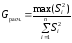, (5.7)

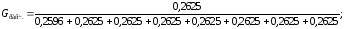
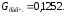
По табл. 3, прил., [2], или таблицам критических значений коэффициента Кохрена, [3] находим: G_табл = 0,4377 (приn= 8;f= 4 – 1 = 3;q= 0,05). Соответственно, имеем:G_расч = 0,1252 <G_табл= 0,4377, значит, гипотеза об однородности дисперсий принимается.

5.6. Вычисляем оценку дисперсии, характеризующей ошибку эксперимента S²{y}:

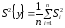, (5.8)

;

.

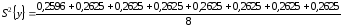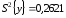5.7. Вычислим оценки дисперсий коэффициентов регрессии:

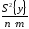
S²{b_i} = 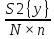, (5.9)

S²{b_i} =

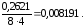
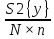
5.8. Оценка значимости коэффициентов регрессии проводится с помощью критерия Стьюдента:

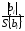
t_расч.i = 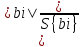, (5.10)

_S{b_i} = 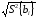, (5.11)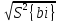

S{b_i} = .

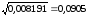t_расч.1 = 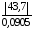= 482,9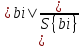;t_расч.2 = = 1293;t_расч.3 = 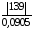= 1536;

t_расч.12 = 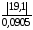= 211;t_расч.13 = 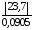= 262;t_расч.23 = 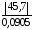= 505;

t_расч.123 = 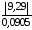= 102,6.

По табл. 2, прил., [2], для числа степеней свободы, связанного с оценкой дисперсии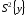,f_y = n·(m – 1) = 8·(4 – 1) = 24 и уровня значимостиq = 0,05 берётсяt-отношение. Имеем:t_табл = 2,06. Видно, что

t_расч.1, t_расч.2, t_расч.3, t_расч.12, t_расч.13, t_расч.23, t_расч.123 > t_табл,

следовательно, все коэффициенты регрессии – b₁, b₂, b₃, b₁₂, b₁₃, b₂₃, b₁₂₃ – являются значимыми.

5.9. Проверка адекватности:

S_ад = 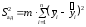, (5.12)

где       – среднеарифметическое значение результатов i-ой серии дублированных опытов;

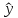
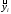– значение выходной величины в i-м опыте, предсказанное уравнением регрессии;

m – число дублированных опытов.

5.10. Вычисляют числа степеней свободы f_ад, связанных с дисперсией адекватности

f_ад = n – p, (5.13)

где     n – число основных опытов плана (8).

p – число значимых коэффициентов регрессии (7). Тогда:

f_ад = n – p = 8 – 7 = 1.

5.11. Расчётное значение критерия Фишера:

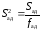, (5.14)

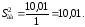
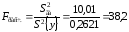. (5.15)

Табличное значение F_табл= 2,78 для числа степеней свободы для числителяm·(n–p) = 4·(8 – 7) = 4 и знаменателяn·(m – 1) = 8·(4 – 1) = 24 и уровня значимостиq= 0,05. ПосколькуF_расч >F_табл, гипотеза об адекватности математической модели принимается.Это может быть связанно либо с экспериментальными ошибками, либо с неправильно выбранной моделью.