Статистический анализ случайных ошибок

При проведении серии измерений некоторой физической величины (например, длины, с помощью линейки или силы тока с помощью амперметра) из-за случайных ошибок отдельные значения x₁,x₂, и т. д. неодинаковы.

Абсолютнаяпогрешность определяет границы интервала, внутри которого с некоторой вероятностью заключено «истинное значение» искомой величины, и она равна взятой по модулю разности между «истинным значением» измеряемой величины и его приближенным значениемx_i.

Но так как «истинное значение» измеряемой величины остается неизвестным, то в качестве наилучшего значения искомой величины принимают среднее арифметическое:

(1)

где x_i–i-е измеренное значение,an- общее число измерений. Символозначает суммирование отi=1доi=n.Абсолютная погрешность отдельногоi-го измерения запишется тогда так

или.

Малый разброс измеренных значений относительно среднего значения означает высокую точность.

Относительнойпогрешностью_xназывается отношение абсолютной погрешностик значениюx_ист, т.е.

.

В отличие от абсолютной погрешности, которая имеет такую же размерность, как и сама величина x, относительная погрешность является безразмерной величиной (её выражают или в долях единицы, или в процентах).

Для оценки величины случайной ошибки (погрешности) измерения обычно используют величину - дисперсию измерения (стандартное отклонение)

, (2)

где n – общее число измерений.

Если стандартное отклонение мало, то разброс измеренных значений относительно среднего значения является малым, следовательно, точность измерения высокая. Заметим, что стандартное отклонение является всегда положительным и имеет ту же размерность, что и измеренные значения.

Используя всю совокупность измерений, мы, естественно, находим искомое значение измеряемой величины с лучшей точностью, чем это можно сделать с помощью одного измерения. Причина улучшения заключается в том, что положительные и отрицательные ошибки частично компенсируются при усреднении результатов нескольких измерений.

Поэтому в качестве меры погрешности результатов измеренийвеличиныx(или неопределенности среднего значения ) принимаютстандартное отклонение от среднегоS_n, которое часто называют средним квадратичным отклонением илистандартной погрешностьюи определяют как

.(3)

Для более полного обсуждения разброса или распределения измеренных значений полезно рассмотреть нормальное или Гауссово распределение.

Нормальное или Гауссово распределение

На рис. 2ав виде диаграммы показано распределение результатовnизмерений некоторой физической величиныxотносительно среднего значения . Ось абцисс разбита на равные интервалы ширинойx. Высота каждого столбика диаграммы показывает количествоN(x) близких результатов измерений, попадающих в интервалxс центром в точкеx. Пунктирная кривая (которая здесь не является симметричной) вычерчена, чтобы показать зависимость числа отсчетовN(x) отx при относительно небольшом числе измерений.

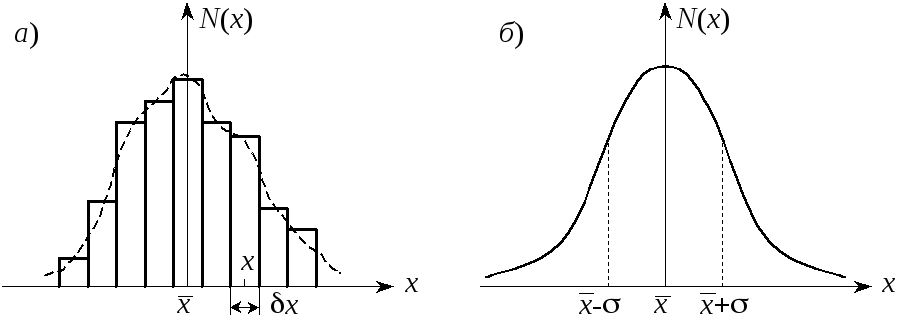
Рис. 2.

Если число измерений nстановитсяочень большим, то результаты измерений стремятся к симметричному распределению около среднего значения (рис. 2б). Как показывается в теории вероятности, в идеальном случае такая кривая описывается аналитическим выражением

, (4)

где n- очень большое число измерений, - среднее значение, а- стандартное отклонение, определяемое по формуле (2) при условииn . Величина²называетсядисперсией. Уравнение (4) представляет собойраспределение Гауссаилинормальноераспределение.

Для большого числа измерений nраспределение Гаусса описывает теоретическое распределение измеренных значенийxотносительно среднего значения . Если измерения выполняются с высокой точностью, тобудет малым, и нормальное, или Гауссово, распределение будет иметь острый пик приx= (рис. 3).

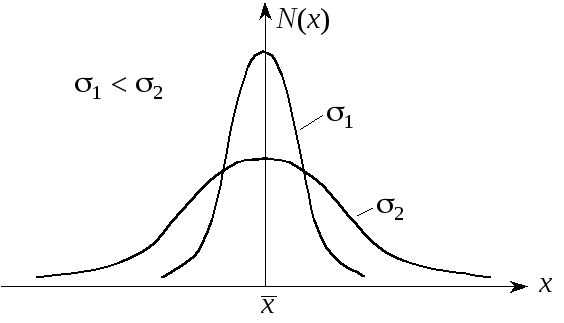
Рис. 3.

Разделив обе части уравнения (4) на nи определивN(x)/n какР(x), имеем:

. (5)

Выражение (5) имеет смысл плотности вероятности того, что в результате измерения мы получим значение х. Таким образом, вероятность того, что измеренное значениеxбудет лежать в некотором интервалеx₁<x<x₂, определяется площадью под соответствующим участком кривой:

.

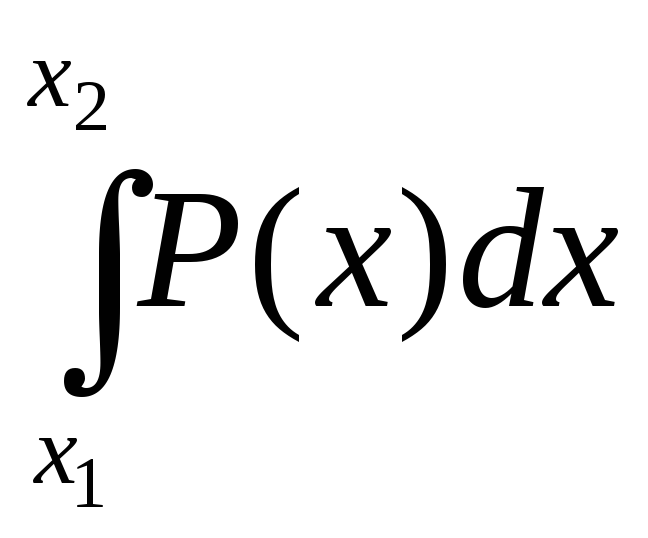Заметим, что наиболее вероятным значением, которое можно ожидать в результате измерения, являетсясреднее значение. Следует также отметить, что полная площадь под кривой, представляющей функциюP(x), всегда равна единице:

.

Особенностью распределения Гаусса является то, что 68% всех результатов измерений попадают в интервал от до, 95% всех результатов измерений попадают в интервал отдо, а 99,7% всех результатов измерений попадают в интервал отдо. Другими словами, с вероятностью 0,68 истинное значение величиныxлежит в интервале, с вероятностью 0,95 – в интервале, и т.д.

Следует иметь в виду, что распределение Гаусса не является единственно возможным. Могут существовать и другие виды распределений, например, распределение Пуассона, экспоненциальное распределение, ²-распределение и т.д. Тем не менее, нормальное распределение встречается достаточно часто, причём все остальные распределения в пределе (приn) переходят в распределение Гаусса.

На практике, однако, число измерений обычно сравнительно невелико. В этом случае для повышения достоверности результатов измерений следует при оценке погрешности пользоваться модифицированными формулами. Так, абсолютная погрешность xизмеряемой величиныxпри относительно малом (скажем, 10 - 100) количестве измерений определяется как:

, (6)

где t_,n– коэффициент (коэффициент Стьюдента), зависящий от числа измеренийnи от величины доверительной вероятности. Значения коэффициентовt_,nдля некоторых различных значенийnиприведены в табл. 1.- полная абсолютная погрешность или доверительный интервал, внутри которого находится истинное значение величины.

В соответствии с действующими государственными стандартами рекомендуется при оценке погрешностей пользоваться доверительной вероятностью = 0,95.

Таблица 1. Коэффициенты Стьюдента

n		0,90	0,95	0,98
2		6,31	12,71	31,82
3		2,92	4,30	6,96
4		2,35	3,18	4,54
5		2,13	2,78	3,75
6		2,02	2,57	3,36
7		1,94	2,45	3,14
8		1,90	2,36	3,00
9		1,86	2,31	2,90
10		1,83	2,26	2,82
12		1,78	2,18	2,68
15		1,75	2,13	2,60
30		1,70	2,04	2,46
50		1,68	2,01	2,40
100		1,66	1,98	2,36

Таким образом, окончательный результат измерений запишется в виде:

ед. измерений, (), (7)

где xопределяется из выражения (6). Запись (7) означает, что истинное значение величиныx с вероятностьюнаходится в интервале (доверительном интервале) значений отдо.