Metodichki / Векторная алгебра

z			M1					1zA 1zB															4 3 1 1											13					,			M	1	(	7		,	4		,		13			).
								1 1																	4 1							5												5 5 5
x	M4						2xA 2xB																	1 2 4 ( 1)																2	;
								2 2																		1 4						5
y		M4					2 yA 2 yB																		1 1 4 0										1			;
								2 2																	1 4							5
z	M4				2zA 2zB																	1 3 4 1											7				,					M	4	(		2			,		1		,	7		)
								2 2																	1 4							5															5 5 5
																										,						служат сторонами треугольника ABC.
				1.5. Векторы									AB						,						BС		СA
Выразить через									a	,				и						c				векторы, совпадающие с медианами треугольника:
												b

AB 2a , BС b , СA 3c ;

Решение:

Воспользуемся свойством медианы: делит противолежащую сторону

пополам и правилом «замыкания ломанной». Выразим медиану AM линейной комбинацией известных векторов. Для этого необходимо выйти из точки A и прийти в точку M по сторонам треугольника (Рис. 1.7):

B

P M

A N C

Рис. 1.7

Т.е. AM AB BM AB 1 BC 2a 1( b) 2a 1b .

																											2						1	2												1	2														1
	Или																																					3			с						(						) 3					с								.
					AM							AС							СM									СA							BC
																																																		b														b
	Аналогично:																										2							2													2
													1														1		3																											2				a					1		3	c	;
		BN					BC								CA								b								c	,							BN						BA						AN
																											2
	2																																														2
		CP				CA						AP				3				c				a		,										CP				CB				BP												a	.
																																																					b

11

§2.1 Скалярное произведение векторов

Скалярным произведением векторов

a

и

называется число,

b

обозначаемое

a

b

или (

a

,

b

) и вычисляемое по формулам:

a

a

a

1)

b

b

cos(

,

b

);

(2.1)

2)

a

a

пр

пр

a

;

(2.2)

b

а

b

b

b

3)

a

axbx ayby azbz;

(2.3)

b

Основные свойства скалярного произведения:

1.a b b a - коммутативность;

2.

(

a

) b (

a

b)

a

( b)

-

ассоциативность относительно

числового множителя;

3.

(

)

- дистрибутивность;

a

b

c

a

b

a

c

a

a

a

2

a

2, откуда

a

,

4.

(

a

,

a

)

(2.4);

В координатной форме:

a

(ax)2 (ay )2

(az )2

(2.5);

5.

0

векторы

ортогональны тогда

и только

a

b

a

b

тогда, когда их скалярное произведение равно нулю.

Физическое приложение: работа равнодействующей силы F по прямолинейному перемещению точки вдоль линии, определяемой вектором

S , вычисляется по формуле:

A F S

Используя формулы скалярного произведения можно выразить:

a

b

cos(

a

,

)

a

b

(2.6) ,

пр

a

(2.7).

b

b

b

a

b

§2.2 Практикум

	2.1.									Вычислить:																a				2,									2,				(	a			)2, (4				a														) (			a				2								).
																																					b									b																b														b
			a				2,																																									a		5,
1)																3, (				a	,			b			)										;						2)													b					2, (											a	,		b		)
												b
			a																														3															a
							4,																																											1,
3)																3, (				a			,		b			)												;			4)												b					3									3		, (				a				,		b			)
												b
																																			3
			a																																3													a		1,
5)								2					,						4, (			a				,			b		)											;	6)															2										3		, (				a		,			b				)
														b																																							b
																																			4
		a			2																																											a		2
7)									2			,							3, (				a			,				b		)									;		8)											3									,		b		4,(								a			,				b			)
																b
																																			4

2

;

3

;

6

;

6

5 ;

6

12

			a		3																				a			7,															2
	9)					2	,		b		2, (	a		,	b		)				;	10)												1, (			a		,	b		)		.
																																b
																			4																								3
																2
	2.2.												AB							2			, пр						AB	, cos(					AB	,		CA			) если:
						Вычислить:												,	AB			AC
																								BC

1)А(6; 1; 2), B(5; 3; 2), C(7; 0; 4);

2)А( 2; 4;1), B(3; 0; 1), C(1;8; 3);

3)А(0; 2; 5), B(7;1; 4), C(1; 3; 6);

4)А(6; 5; 3), B(8; 5; 3), C( 2; 3;1);

5)А(4; 6;1), B( 1; 4; 2), C(5; 3;1);

6)А(1; 4; 7), B( 3; 5; 2), C(4; 0; 5);

7)А(5; 4; 3), B(2; 1; 7), C(1; 0; 5);

8)А(4; 2; 1), B(0; 1; 2), C(7; 3; 5);

9)А( 1; 5; 3), B(4; 2; 7), C( 1; 1; 0);

10)А(8; 0; 7), B(1; 1; 2), C(4; 1; 0).

2.3.При каком значении вектора a и b ортогональны?

1)a i 3j 5k , b 7i 4k ;

2)a 7i j 8k , b 4j 5k ;

3) a 5i j k , b 2i 4k ;

4) a 3i j k , b 5i 3k ;

5)a i 2j k , b 3i 7 j;

6)a 2i 3j, b i 4j k ;

7) a i j k , b 2i 4k ;

8)a 5i j 3k , b 2j k ;

9)a 7i j k , b 4j 5k ;

10)a 3i k , b i 4j 2k ;

2.4. Векторы a и b заданы линейной комбинацией векторов m и n.

										a																		a																						m				1,						n				2									, (							m				,		n		)					3				.
Вычислить:															b				,													,							b			, если																													2
																																																																4
1)		a	2		m						n		,					b												m				3						n			;					2)									a								m		5					n		,		b					2						m			3					n		;
3)		a	4				m		2								n			,						b			3								m							n		;		4)									a								m		2					n			,		b				4							m			3					n		;
5)		a	2		m			3					n		,						b														m			4						n		;		6)									a	6								m			3					n	,				b				2						m						n			;
7)		a		m		2					n					,		b					3									m								n			;					8)									a	4								m						n			,		b				3						m			2						n		;
9)		a	3				m							n		,						b			5										m			2						n		;				a				10)				a			3						m			2					n			,				b			4					m				2					n	.
			2.5. Найти проекцию вектора																																																	по направлению вектора																																					b		.
								1)					a																				5														,
																																										k
																																																	b
																3i																								j											6i					5j 3k ;

13

2)

a

4i j 6k ,

b i 2j 3k ;

3)

a

4i

j 2k ,

b 7i 3j 4k ;

4)

a

8

,

b

4k

3i

j

4i

2j k ;

5)

a

5

,

b

3k

2i

j

2i

6j k ;

6)

a

3

,

4

;

k

b

7k

5i

j

2i

j

7)

a

5

,

;

7k

b

2k

3i

j

4i

j

8)

a

2i

3j k ,

b 5i

3

j

8k ;

9)

a

2

,

5k

b

4k

;

3i

j

i

j

10)a i 2j 3k , b 5i j 2k ;

2.6.Найти косинус угла между векторами m и n, если m n 1, а

векторы a и b взаимно ортогональны.

1) a m 3n, b 5m 2n; 3) a m 2n, b 3m 4n; 5) a m 4n, b 5m n; 7) a 2m 3n, b 5m n ; 9) a 3m n, b m 2n ;

2) a 4m n, b m 3n ; 4) a 2m 5n , b 3m 2n; 6) a 3m 2n, b m n; 8) a 2m 4n, b m 3n; 10) a 4m 2n, b m n;

2.7. Найти косинус угла между векторами a и b , если:

1)		a		1,								6,	(2		a								)2 (3									a													)2 15;
						b														b																				b
2)		a		2,								4,	(	a			2											)2 (			a												)2 24;
								b														b																	b
3)		a		3,								4,	(	a			3										)2 (2						a			2																)2 16;
							b														b																										b
4)		a		4,								2,	(3			a		5												)2 (						a		4																)2 28;
								b																			b																										b
5)		a		5,								3,			(2	a										)2 (3						a														)2 36;
							b														b																				b
6)		a		2,								4,	(	a			4											)2 (2						a															)2 15;
								b														b																					b
7)		a		3,								5,	(3		a								)2 (6									a			$															)2 27;
							b												b																										b
8)		a		4,								6,	(2				a	3											)2 (7						a																	)2 35;
								b																		b																						b

9)a 2, b 3, (a 2b)2 (6a 2b)2 42;

10)a 5, b 6, (5a b)2 (4a b)2 33;

§2.3 Решение типового задания.

14

2.1. Вычислить:							a		2,					2, (					a						)2,	(3	a	2		) (	a			). Если
												b												b					b				b
		a		3
известно, что					2		,	b			5,		(		a	,	b	)					.
																					4

Решение:

Вычислим значение a2 и b 2, используя свойство скалярного квадрата 4:

a	2		a		2	(3	2)2 18,			2						2	(5)2	25.
									b				b

Для вычисления квадрата суммы векторов, используем формулу сокращенного умножения:

(	a			)2			2								2					2																	2
						a		2	a									a			2		a						cos(	a	,		)
			b									b		b													b					b			b

18 2 3																			5							2				25 73.
																2
																										2
																																																a												a
При вычислении																										произведения (3																									2				b			) (									b	)			будем использовать
свойство дистрибутивности 3.
(3		a			2					) (						a									) 3						a			2 3										2								2							2.
								b																b															ab									ba										b
Применяя свойство коммутативности 1., получаем:
3	a		2 3											2											2								2 3				a			2									2							2
									ab											ba										b
																																													ab								b
					a		2					a															a															2 3 18 3																							5							2		2 25 134
3																						cos(							,					) 2																												2
																		b														b							b
																																				2																																			2
							2.2. Вычислить:																												AB											2								, пр												AB			,			cos(			AB	,	CA	) если:
																																						,					AB								AC
																																																													BC
А(1; 2; 3), B( 1; 0;1), C(2; 4;																																										5).

Решение:

Определим координаты векторов AB, AC, BC:

AB ( 1 1; 0 2;1 3) ( 2; 2; 2);

AC (2 1; 4 2; 5 3) (1; 2; 8);

BC (2 ( 1); 4 0; 5 1) (3; 4; 6);

Используя свойство скалярного квадрата 4. и формулу (2.3), найдем AB2:

AB2 AB 2 ( 2)2 ( 2)2 ( 2)2 12.

Используя свойство 2. и формулу (2.3), вычислим скалярное произведение

AB 2AC: 2(AB AC) 2 2 1 ( 2) 2 ( 2) ( 8) 20.

При вычислении проекции вектора AB на вектор BC необходимо воспользоваться формулами (2.3), (2.5) и (2.7).

15

пр

AB BC

2 3 ( 2) 4 ( 2) ( 6)

2

.

AB

BC

BC

32 42 ( 6)2

61

и

, используем

При вычислении косинуса угла между векторами

AB

AC

формулы (2.3), (2.5) и (2.6).

cos(AB,CA) AB CА ;
АB СА
Вектор СА является противоположным к AC, поэтому:
2 ( 1) ( 2) ( 2) ( 2) 8			10 .
( 2)2 ( 2)2 ( 2)2	( 1)2 ( 2)2 82		12 69

2.3.Установить, при каком значении вектора a и b

ортогональны, если

a

4i 2j k ,

b i j 3k .

Решение:

Согласно свойству 5., векторы ортогональны тогда и только тогда,

когда их скалярное произведение равно нулю: a b 0. Векторы заданы линейной комбинацией базисных векторов. В координатной форме их можно

переписать так: a (4; 2; ), b (1; 1;3). Приравняв нулю их скалярное произведение вычисленное по формуле (2.3), получим уравнение относительно неизвестной величины :

a b 4 1 2 ( 1) ( ) 3 0, 2 3 0, откуда 2.

3

Или a b (4i 2j k) (i j 3k) 0.

Раскрывая скобки по правилу умножения многочленов и применяя свойство ортогональности для базисные векторов i, j, k , мы получим равенство

a b 4i i 2j j k 3k 0. Откуда a b 4 2 3 0, 2.

3

2.4. Векторы a и b заданы линейной комбинацией векторов m и n:

a

5

m

n

a

, b 2

m

3

n

. Вычислить:

a

b ,

,

b

, если известно,

что

m

1,

n

2

3

2

,

(

m

,

n

)

.

4

.

Решение:

a

(5

m

n

)(2

m

3

n

).

Применяя

свойство

дистрибутивности

и

b

коммутативности

скалярного произведения

векторов

получим:

a

10

m

2 13

m

n

3

n

2

10

m

2 13

m

n

cos

3

3

n

2

b

4

16

10 12 13 1 22 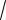2 3 (22)2 40. 2

При вычислении модулей векторов, пользуемся следствием из свойства 4.

a (а,а) (5m n)(5m n) 25m2 10m n n2

		25 12 10 1 2				2	(2	2)2		;
			2						53
						2

b(b,b) 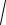(2m 3n)(2m 3n)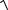 4m2 12m n 9n2

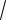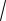4 12 12 1 22 2 9(22)2 52.

	2
2.5. Найти проекцию вектора a по направлению вектора b , если
a 3i 2j k ,	b i 4j 2k .

Решение:

При решении используем формулы (2.7), (2.3) и (2.5). Запишем вектора в

координатной форме: a (3; 2; 1), b (1; 4; 2). Тогда

прb a a b 3 1 2 ( 4) ( 1) 2 7 .
b	12 ( 4)2 22	21

2.6. Найти косинус угла между векторами m и n, если m n 1, а

векторы a и b взаимно ортогональны: a 2m 4n, b m 3n .

Решение:

Найдем скалярное произведение векторов a и b .

a b (m n)( m 3n) m2 2m n 3n2

Т.к. векторы a и b ортогональны, то их скалярное произведение равно нулю.

m2 2m n 3n2 0.

Из последнего равенства выразим скалярное произведение векторов m и n

m2 3n2 2m n;

						m		2	3		n		2	2		2
m		n													1 1 3 1		1.
								2							2

Применяя формулу для определения косинуса угла между векторами (2.6), получим, что

							m n											1
cos(	m	,	n	)															1.
							m						n
																	1 1

2.7. Найти косинус угла между векторами a и b , если известно, что

a		2,				1,	(2	a			)2 (	a	3		)2 3.
				b						b				b
							17

Решение:

Раскроем скобки в заданном выражении и выразим из него скалярное

произведение векторов a и b .

(2a b)2 (a 3b)2

4a2 4a b b2 a2 6a b 9b2 3;

3a2 2a b 8b 2 3;

								3 3			a			2 8								2			3 3 22 8 12						1	.
	a																				b
			b
												2
																											2				2
Тогда косинус угла определяется как:
											a b											1						1
cos(				a		,	b		)																				.
										a						b							2 2 1				4

18

§3.1 Векторное и смешанное произведение векторов.

Упорядоченная тройка некомпланарных векторов a, b, c с общим началом в точке O называется правой, если кратчайший поворот от вектора a к вектору b вокруг вектора c происходит против часовой стрелки (Рис. 2.1). В противоположном случае данная тройка называется левой (Рис.2).

c

c

b

a

O

O

a

b

Рис. 1

Рис. 2

Векторным

произведением

векторов

a

и

называется

вектор

c

,

b

обозначаемый

c

a

b

[

a

,

b

], и удовлетворяющий трём свойствам:

1)

модуль

вектора

c

равен площади S параллелограмма

a

построенного на векторах

и

b

:

c

a

b

sin(

a

,

b

) S

(3.1)

2)c a и c b ;

3)a, b, c - образуют правую тройку векторов (Рис. 3).

c a b

b S O a

Рис. 3

Основные свойства векторного произведения:

1)

a

b b

a

- антикоммутативность;

2)

(

a

)

b

(

a

b

)

a

(

b

) - ассоциативность относительно

числового множителя;

3)a (b c) a b a c - дистрибутивность;

4)a b 0, тогда и только тогда, когда векторы коллинеарны a || b .

Отсюда следует, что векторный				квадрат также равен нулю:
a		a	0.	(3.2)

19

Условие коллинеарности векторов можно записать через

пропорциональность их координат:

a

x

ay

a

z

.

by

bx

bz

(3.3)

a

ax; ay; az ,

координатами

Если векторы

и

b

заданы

а

b bx;by; bz то векторное произведение a b определяется формулой:

i

j

k

с

a

ax

ay

az

(3.4)

b

icx jcy kcz

bx

by

bz

Физическое приложение: Вращающий момент M силы F ,

приложенной к точке B тела, закрепленного в точке A: M AB F .

Смешанным произведением векторов a, b, c называется число,

обозначаемое (a b)с (a,b,c). Основные свойства смешанного произведения:

1)При ациклической перестановки векторов, смешанное произведение меняет знак на противоположный

abc bca cab bаc aсb

2)Модуль смешанного произведения равен объему параллелепипеда

построенного на векторах a, b, c :

abc

V

(3.5)

3)Смешанное произведение векторов равно нулю тогда и только тогда,

когда векторы компланарны

abc

0

a

, b,

c

.

(3.6)

a

,

,

c

заданы координатами

ax; ay; az

,

Если векторы

b

а

bx;by; bz ,

с

сx; сy; сz то

a

с

b

смешанное

произведение

b

ax

ay

az

определяется формулой:

a

bc

bx

by

bz

(3.7)

cx

cy

cz

§3.2 Практикум.

3.1. Вычислить,

(2

m

n

) (4

m

2

n

)

.

1)

m

3

,

n

2, (

m

,

n

)

;

2)

m

4,

n

1, (

m

,

n

)

;

3

6

20