Лекции Гирдрогазодинамика / 11-13

11. Скорость звука в газе. Распространение слабых возмущений в потоке газа

Для выяснения особенностей движения газа оказывается весьма важным соотносить его скорость со скоростью распространения в газе слабых (или малых) возмущений. Слабые возмущения в упругой среде, в частности – в жидкости и газе – это механические колебания частиц среды с малыми амплитудами; их распространение в среде носит волновой характер. Наиболее известным примером таких возмущений являются звуковые колебания (волны), чем и определяется их название – звуковые волны или просто звук. В жидкостях и газах эти возмущениях представляют собой упругие продольные колебания малых разрежения – сжатия. Распространение звуковых волн в пространстве не приводит к переносу вещества в нем.

Скорость распространения в среде волны слабых возмущений называется скоростью звука – а. Скорость звука в газе зависит от физических свойств и термодинамического состояния газа и обычно не зависит от часто –ты и амплитуды колебаний; при этом распространение звука будет баротропным процессом, для которого р=р(ρ). Можно показать, что тогда

(11.1)

Таким образом, скорость звука в газе определяется зависимостью р=р(ρ), т.е. характером баротропного процесса распространения слабых возмущений в газе. Распространение звука в газе – быстропротекающий процесс, который практически не сопровождается теплообменом и диссипацией, поэтому его можно считать изоэнтропическим процессом. Таким образом, используя уравнение (10.8) в виде

р=с, с=p/=p₀/=const,

найдем

.

Подставляя это в (11.1), получим формулу Лапласа

(11.2)

или, учитывая (10.1,б),

. (11.3)

Формулы (11.1) – (11.3) получены для покоящегося газа. Они применимы и в случае движущегося газа, если под а понимать местную скорость распространения слабых возмущений относительно движущегося газа в данной точке потока, рассматривая скорость самого потока V как переносную, т.е. а~Vотн, V~Vпер. По теореме о сложение скоростей в сложном движении Vабс=Vпер+Vотн. Применим этот подход к распространению звука в потоке газа.

Рассмотрим однородный поток с постоянной скоростью V; пусть некоторой неподвижной точке О происходит слабое возмущение, распространяющееся по газу со скоростью а во все стороны как сферическая волна. Тогда абсолютная скорость возмущения запишется как вектор V+an, где n- произвольный единичный вектор, и будет зависить от направления n и от соотношения между V и а. Если V < а, то, как видно из рис.?, возмущение будет распространяться во все стороны от исходной точки О; например, по направлению потока со скоростью V+(а›0), а против потока со скоростью V-(а‹0). Иное дело при V›а. Тогда против потока возмущение распространяться не может. Геометрическое место возмущения в каждый момент времени t представляет собой сферу радиуса at с центром, расположенным на расстоянии V t по потоку от точки О. Легко видеть, что сгибающей таких сфер является конус с углом полураствора , причем sin=a/V.(рис?). Этот конус называется конусом Маха, отношение М = V/а называется числом Маха, а угол =arcsin(1/М) – углом Маха; конус Маха является границей распространения слабых возмущений в однородном сверхзвуковом потоке газа.

12.Характерные параметры и скорости течения идеального газа.

Числа М и λ

Рассмотрим энергоизолированное течение идеального газа, для которого q_нар=0 и а_тех=0. Уравнение энергии такого движения (см.(7.5)), записанное в виде

вдоль потока,

используя различные эквивалентные выражения для энтальпии h и полной энтальпии h_0, вытекающие из (10.3), (10.4) и (11.2), можно записать в следующих формах:

, (12.1)

, (12.2)

, (12.3)

где Т₀, р₀, ρ₀, и а₀ =называются параметрами торможения, так как они соответствуют точке потока, в которой V=0, – точке торможения (или исходному состоянию покоя газа при рассмотрении истечения газа из резервуара большого объема). Эти параметры характерны для всего рассматриваемого потока, поскольку они сохраняют свои значения независимого от положения точки торможения в потоке (для р₀ и ρ₀ это справедливо в предположении изоэнтропического торможения).

Из уравнения (12.1)-(12.3) следует, что модуль скорости V в потоке не может превышать величину

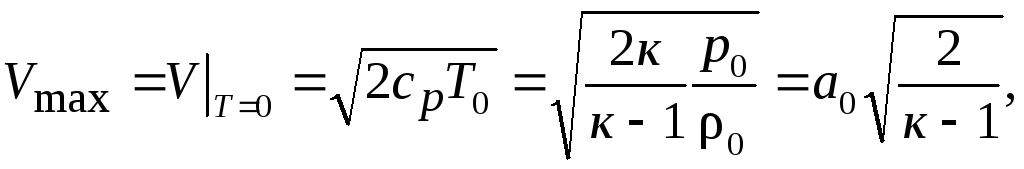(12.4)

которую надо понимать как теоретическую верхнюю границу для скорости в данном потоке. Физический смысл V_max можно представить, схематично рассмотрев истечение газа из резервуара большого объема, где он находится в состоянии покоя (т.е. V=0, Т=Т₀, р=р₀, ρ=ρ₀, а=а₀ ), по некоторому каналу в пустое пространство- вакуум, где Т=0, р=0, ρ=0, а=0. Естественно предположить, что вследствие падения давления вдоль канала скорость потока V будет увеличиваться, стремясь к V_max , а скорость звука а из-за охлаждения газа будет уменьшаться, стремясь к нулю (см. рис.?), так же, как и параметры Т, р и ρ. В некотором сечении канала величины V и а при этом неизбежно сравняются – это сечение (или точка) в потоке называется критическим ~ х=х_*; соответствующие значения скорости V = а=а_* и параметров состояния Т=Т_*, р=р_*, ρ=ρ_* также называются критическими. Эти величины образуют еще один набор характерных параметров. В газовой динамике параметры торможения, критические параметры, а также V_max часто служат масштабами, с которыми принято соотносить текущие (местные) значения соответствующих величин.

Так как в критической точке V = а=а_*, то из уравнения (12.3) следует

,

откуда получаем

. (12.5)

Теперь уравнению энергии (12.3) можно придать еще такую форму

(12.6)

В газовой динамике часто используются безразмерные параметры: число Маха М = V / a и приведенная скорость λ = V / a_*. Между значениями М и λ имеет место взаимно однозначная связь, которая получается из (12.6). Поделив это равенство на V ², будем иметь уравнение

,

легко разрешаемое относительно и М. Таким образом, получим

. (12.7)

Отметим, что при 0≤V<V_max

0≤М<, 0≤λ<λ_max ,

где

. (12.8)

Газовые потоки разделяются на два класса: при V<а_*<а (М<λ<1) поток называется дозвуковым, при V>а_*>а (М>λ>1) поток является сверхзвуковым. Как будет видно в дальнейшем, свойства потока этих двух классов качественно различаются между собой.

13. Изоэнтропические формулы и газодинамические функции

Для изоэнтропического движения газа можно составить простые соотношения между относительными значениями параметров состояния Т, ρ, р, с одной стороны, и безразмерными скоростями потока М или λ – с другой.

Из уравнения энергии в форме (12.1), поделенного на С_рТ, найдем

.

Учитывая, что С_рТ=а² /(к-1) и V/ а = М, получим в итоге

. (13.1)

Используя изоэнтропическую связь термодинамических параметров (10.9^’) и (10.9^’’), отсюда легко установить соотношения

, (13.2)

, (13.3)

При малых значениях М из (13.2) с помощью разложения Тейлора найдем

и, отбрасывая малую величину 4-го порядка О(М⁴), получим приближенное соотношение

, (13.4)

согласно которому при малых ускорениях газа из состояния покоя его плотность уменьшается, но незначительно; число Маха М при этом можно рассматривать как меру сжимаемости (точнее – расширения) газового потока: так, при М ≤ 0.1 плотность газа уменьшается не более чем на полпроцента.

Аналогично устанавливаются зависимость безразмерных параметров состояния от приведенной скорости .

Из уравнения (12.1), поделенного на c_рТ₀ , найдем

.

Сравнивая (12.1)и (12.6), будем иметь , что позволяет предыдущее равенство записать как

, (13.5)

где - безразмерная температура. Введя обозначения безразмерных плотности и давления , аналогично (13,2) и (13.3) будем иметь

, (13.6)

. (13.7)

Между величинами , и имеют место простые связи, которые являются выражением изоэнтропических соотношений (10.8), (10.8'), (10.8'')

и уравнения состояния (10.1,б):

, , (13.8)

Поскольку для реальных газов 1<к<2, то из (13.8) вытекает, что

,

причем знаки равенства здесь имеют место только при , когда и , когда .

Указанные зависимости называются газодинамическими функциями; областью определения этих функций является отрезок , на котором монотонно убывают. Можно отметить, что , , .

Приведем соотношение между критическими параметрами и параметрами торможения потока. Они получаются из (13.1)-(13.3) при М=1 или из (13.5)-(13.7) при :

,,. (13.9)

К этим равенствам присоединяется выражение для критической скорости (12.5) в виде .

Еще одна важная газодинамическая функция определяется как нормированная плотность тока

q= (13.10)

и называется приведенным удельным расходом. С помощью соотношений (13,6) и (13.9) придадим q вид

q=. (13.11)

Легко убедиться, что q(0)=q()=0, q(1)=1, q'(1)=q'=0; функция q(λ) возрастает на интервале 0<λ<1, при λ=1 достигает своего максимума q(1)=1 и убывает при 1<λ<λ_max.

Заменив в (13.11) λ на М посредством (12.7), получим

q=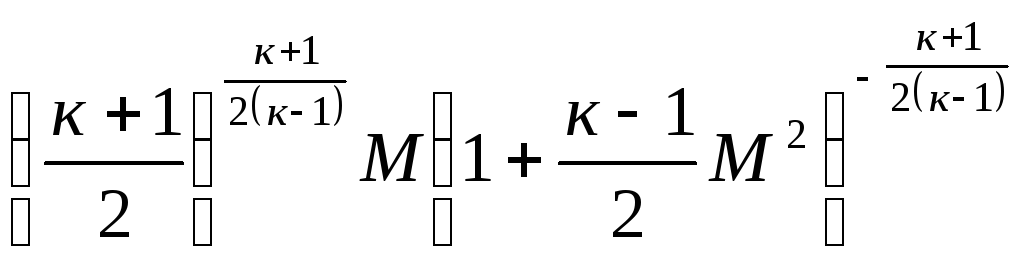. (13.12)

Указанные функции применяются при расчете параметров изоэнтропических потоков; существуют таблицы этих функций, составленные для различных значений показателя изоэнтропы к.